Least square fitting
Using tools
p5.js is an open source designer tool, specializing in drawing
Here are the documents, toolkit and official website (only p5.min.js is used in this article)
Link: https://pan.baidu.com/s/1i5D0OpZ Password: e04v
https://p5js.org/
Fit line
Final effect
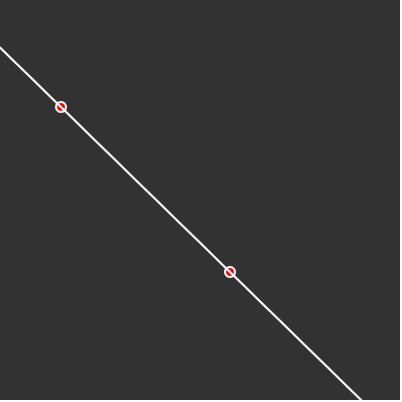

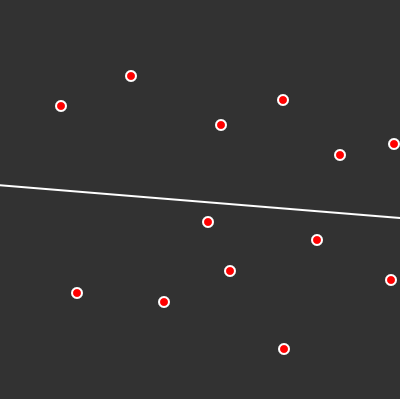
mathematical formula
∑ni=0(x−x¯)(y−y¯)∑ni=0(x−x¯)(x−x¯)
Code JS
var data=[];//Point coordinates
var a=1;//x-factor of fitting line
var b=0;//Changshu b fitting straight line
/**
* Initial function
*/
function setup() {//The initial method of p5.js
createCanvas(400,400);
background(0,3,3);
}
/**
* Linear regression of primary function (coefficient term and constant term)
*/
function linearRegression(){
var xsum=0;//Multiple sum of x
var ysum=0;//Multiple sum of y
for(var i=0;i<data.length;i++){
xsum+=data[i].x;
ysum+=data[i].y;
}
var xmean=xsum/data.length;//Average of x
var ymean=ysum/data.length;//The average of y
var num=0;//Polynomial sum [(mean value of x-x) * (mean value of y-y]]
var den=0;//Polynomial sum [(mean of x-x) * (mean of x-x)]
for(var i=0;i<data.length;i++){
var x=data[i].x;
var y=data[i].y;
num+=(x-xmean)*(y-ymean);
den+=(x-xmean)*(x-xmean);
}
a=num/den;//Coefficient a of y=ax+b
b=ymean-a*xmean;//Coefficient b of y=ax+b
}
/**
* Mouse click
*/
function mousePressed(){
var x=map(mouseX,0,width,0,100);
var y=map(mouseY,0,height,100,0);
var point = createVector(x,y);
data.push(point);
}
/**
* Draw a straight line
*/
function drawLine(){
var x1=0;//If you get (x1,y1),(x2,y2), you can draw a straight line
var x2=100;
var y1=a*x1+b;
var y2=a*x2+b;
x1=map(x1,0,100,0,width);
x2=map(x2,0,100,0,width);
y1=map(y1,0,100,height,0);
y2=map(y2,0,100,height,0);
stroke(255);
line(x1,y1,x2,y2);
}
/**
* Painting (points and lines)
*/
function draw() {
background(50);
for(var i=0;i<data.length;i++){
var x=map(data[i].x,0,100,0,width);
var y=map(data[i].y,0,100,height,0);
fill(255,0,0);//Set fill color
stroke(255);//Set border color
strokeWeight(2);//Set the width of the point
ellipse(x,y,10,10);//Ellipse
}
if(data.length>1){
linearRegression();
drawLine();
}
}Code html
<!DOCTYPE html>
<html>
<head>
<meta name="viewport" width=device-width, initial-scale=1.0, maximum-scale=1.0, user-scalable=0>
<style> body {padding: 0; margin: 0;} </style>
<script src="libs/p5.min.js"></script>
<script src="sketch.js"></script>
</head>
<body>
</body>
</html>Curve fitting (quadratic)
Final effect
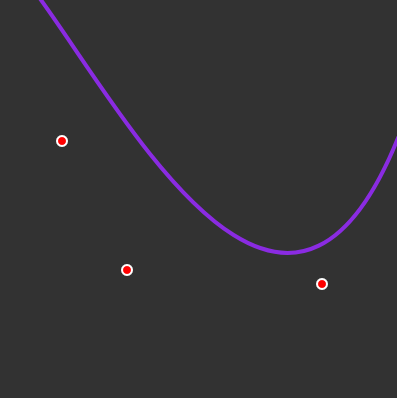
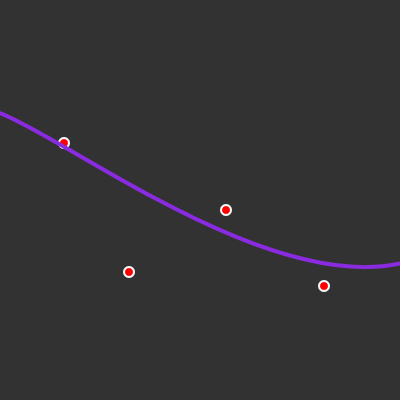

Mathematical formula this formula is a little complicated last screenshot (note p(x), α, β, a)
The formulas of quadratic form and multiple form are consistent. The quadratic function can be extended to many times after being fitted 

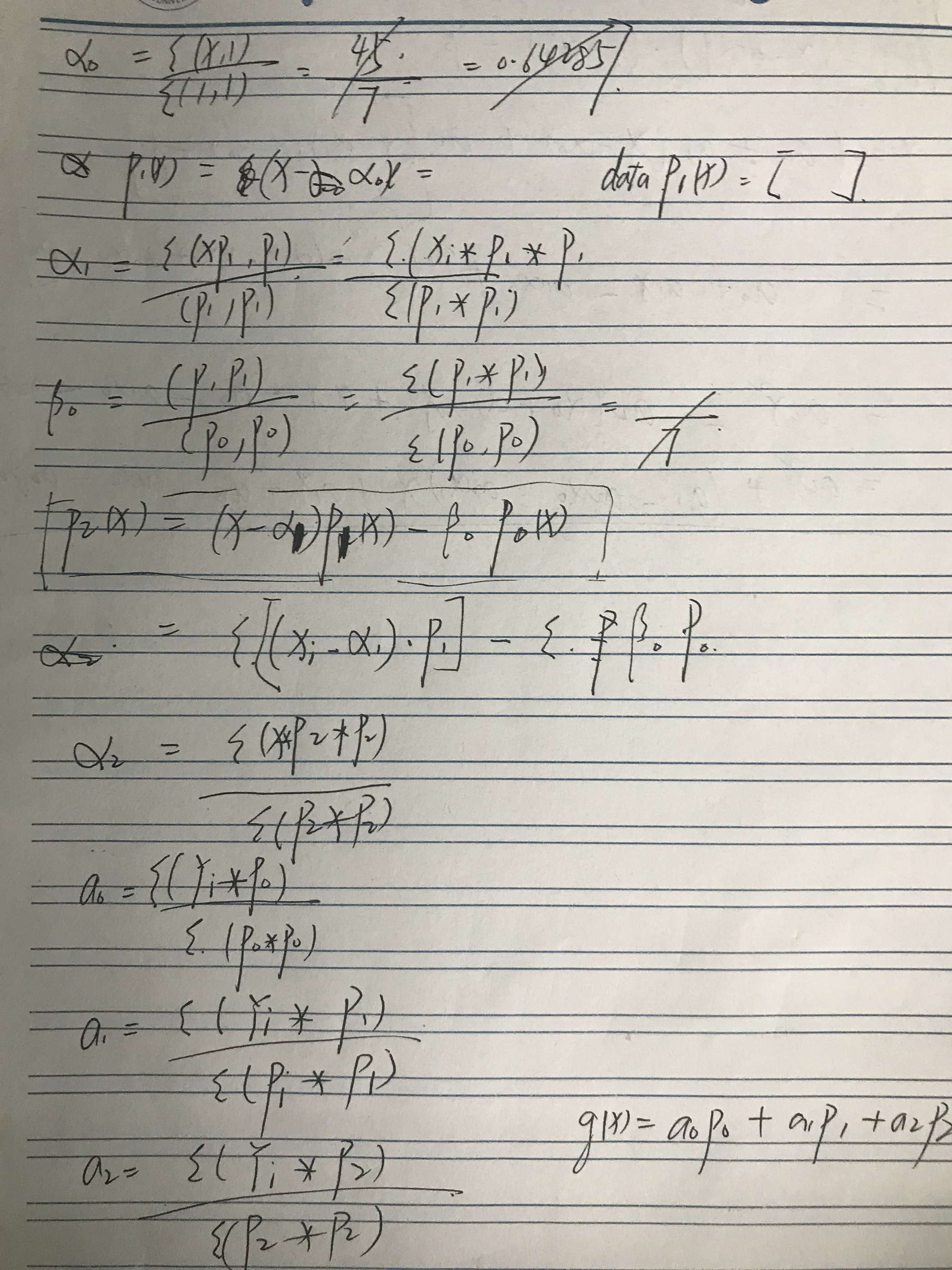
Code JS
var data=[];//Point coordinates
/**
* Initial function
*/
function setup() {
createCanvas(400,400);
background(0,3,3);
}
var alpha0=0;
var alpha1=0;
var a0=0;
var a1=0;
var a2=0;
var beta0=0;
/**
* Quadratic function
*/
function unLinearRegression(){
var xsum=0;//Sum of x
var ysum=0;//The sum of y
for(var i=0;i<data.length;i++){
xsum+=data[i].x;
ysum+=data[i].y;
}
var length=data.length;//p0(x)=1, so the sum of p0(x) is the data length
alpha0=xsum/data.length;//α0
var p1data=[];//p1(x)
var p1p1sum=0;//The sum of p1*p1 polynomials
var xp1p1sum=0;//The sum of x*p1*p1 polynomials
for(var i=0;i<data.length;i++){
var p1=data[i].x-alpha0;
p1p1sum+=p1*p1;
xp1p1sum+=data[i].x*p1*p1;
p1data.push(p1);
}
alpha1=xp1p1sum/p1p1sum;//α1
beta0=p1p1sum/length;//β0
var p2data=[];//p2(x)
var p2p2sum=0;//The sum of p2*p2 polynomials
var xp2p2sum=0;//The sum of x*p2*p2 polynomials
for(var i=0;i<data.length;i++){
var p2=(data[i].x-alpha1)*p1data[i]-beta0;
p2data.push(p2);
p2p2sum+=p2*p2;
xp2p2sum+=data[i].x*p2*p2;
}
//var alpha2=xp2p2sum/p2p2sum;
var fp0=ysum;//The sum of Y * P 0 polynomials
var fp1=0;//The sum of y*p1 polynomials
var fp2=0;//The sum of y*p2 polynomials
for(var i=0;i<data.length;i++){
fp1+=data[i].y*p1data[i];
fp2+=data[i].y*p2data[i];
}
a0=fp0/length;//g(x)=a0*p0(x)+a1*p1(x)+a2*p2(x) quadratic polynomial fitting formula
a1=fp1/p1p1sum;
a2=fp2/p2p2sum;
}
/**
* Draw a curve
*/
function drawCurve(){
var newdata=[];//Quadratic polynomial point data
for(var i=0;i<100;i++){//Generate 100 point drawing curves
var x=i*100;
var pp1x=x-alpha0;
var pp2x=(x-alpha1)*(x-alpha0)-beta0;
var y=(a0+a1*pp1x+a2*pp2x);
/*var y=x*x+90;*/
var point=createVector(x,y);
newdata.push(point);
}
//b=x*x;
var i=0;
noFill();
//Three points form a curve
if(i<newdata.length){
var p1x=newdata[i].x;
var p1y=newdata[i].y;
p1x=map(p1x,0,100,0,width);
p1y=map(p1y,0,100,height,0);
i++;
var p2x=newdata[i].x;
var p2y=newdata[i].y;
p2x=map(p2x,0,100,0,width);
p2y=map(p2y,0,100,height,0);
i++;
var p3x=newdata[i].x;
var p3y=newdata[i].y;
p3x=map(p3x,0,100,0,width);
p3y=map(p3y,0,100,height,0);
i++;
/* var p4x=newdata[i].x;
var p4y=newdata[i].y;
p4x=map(p4x,0,100,0,width);
p4y=map(p4y,0,100,height,0);
i++;*/
var p1 = {x: p1x, y: p1y};
var p2 = {x: p2x, y: p2y};
var p3 = {x: p3x, y: p3y};
//var p4 = {x: p4x, y: p4y};
noFill();
stroke(138, 43, 226);//Curve color violet
strokeWeight(4);//Curve width
curve(p1.x, p1.y, p1.x, p1.y, p2.x, p2.y, p3.x, p3.y);
}
}
/**
* Mouse click
*/
function mousePressed(){
var x=map(mouseX,0,width,0,100);
var y=map(mouseY,0,height,100,0);
var point = createVector(x,y);
data.push(point);
}
/**
* Painting (points and lines)
*/
function draw() {
background(50);
for(var i=0;i<data.length;i++){
var x=map(data[i].x,0,100,0,width);
var y=map(data[i].y,0,100,height,0);
fill(255,0,0);//Set fill color
stroke(255);//Set border color
strokeWeight(2);//Set the width of the point
ellipse(x,y,10,10);//Ellipse
}
if(data.length>2){
unLinearRegression();
drawCurve();
}
}