Background introduction
After learning the SLAM for a period of time, I feel that I have a certain understanding of its principle, and I want to write a demo of motion evaluation between two frames. In this demo, there is no back-end optimization, mapping and loopback detection, only motion estimation between two frames. General idea: using binocular camera, using SGBM algorithm to get the left target disparity map, and then recover the left target depth information, using ORB feature matching between the front and back frames, using RANSAC algorithm to do error matching elimination, using singular value decomposition ICP method to estimate the motion.
After the code is written, the KITTI data set is used for verification, and the 00 sequence pictures in the Odometry module are used. It is found that the estimated motion result is quite different from the KITTI reference value, so what's the matter?
code implementation
1. Internal parameters of camera
Check KITTI's development kit. The camera's intrinsic parameters F X, f y, cx, C Y F X, f y, C x, C YFx, fy, cx, cy and the baseline bbb of binocular are set as follows,
fx=718.856,fy=718.856,cx=607.1928,cy=185.2157
f_x=718.856,f_y=718.856,c_x=607.1928,c_y=185.2157
fx=718.856,fy=718.856,cx=607.1928,cy=185.2157
b=0.54
b=0.54
b=0.54
2. Acquisition of parallax
It is implemented by the Mat GetDisparity(string imgl, string imgr) function. The function name is GetDisparity, and the input parameters are imgl and imgr (the path of left and right figures). It returns the parallax map, which is of the Mat type. The function contents are as follows:
//Obtain parallax of left and right images Mat GetDisparity(string imgl, string imgr){ Mat img_1 = imread(imgl, 0); Mat img_2 = imread(imgr, 0); cv::Ptr<cv::StereoSGBM> sgbm = cv::StereoSGBM::create( 0, 96, 9, 8 * 9 * 9, 32 * 9 * 9, 1, 63, 10, 100, 32); // Magic parameters cv::Mat disparity_sgbm, disparity; sgbm->compute(img_1, img_2, disparity_sgbm); disparity_sgbm.convertTo(disparity, CV_32F, 1.0 / 16.0f); return disparity; }
In this part of the code, CV:: PTR < CV:: stereo sgbm > sgbm = CV:: stereo sgbm:: create (0, 96, 9, 8 * 9 * 9, 32 * 9 * 9, 1, 63, 10, 100, 32); / / the magic parameters are written by referring to the binocular visual code in section 5.4.1 of Dr. Gao Xiang's vision SLAM 14 lectures.
3. Feature matching
The front and back frames are matched by the function vector < vector4d > qhmatch (string img1, string img2). The function name is qhmatch, and the input parameters are img1 and img2 (the path between the left image of the previous frame and the left image of the current frame). The coordinates of the matched feature points are returned
(uimg1,vimg1,uimg2,vimg2)
(u_{img1},v_{img1},u_{img2},v_{img2})
(uimg1,vimg1,uimg2,vimg2)
The type is vector < vector4d >. The function contents are as follows:
//Matching function vector<Vector4d> qhmatch (string img1, string img2){ vector<Vector4d> points; Mat img_1 = imread(img1, CV_LOAD_IMAGE_COLOR); Mat img_2 = imread(img2, CV_LOAD_IMAGE_COLOR); //- initialization vector<KeyPoint> keypoints_1, keypoints_2; Mat descriptors_1, descriptors_2; Ptr<FeatureDetector> detector = ORB::create(); Ptr<DescriptorExtractor> descriptor = ORB::create(); Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create("BruteForce-Hamming"); //--Step 1: detect the corner position of Oriented FAST detector->detect(img_1, keypoints_1); detector->detect(img_2, keypoints_2); //--Step 2: calculate the BRIEF descriptor according to the corner position descriptor->compute(img_1, keypoints_1, descriptors_1); descriptor->compute(img_2, keypoints_2, descriptors_2); //--Step 3: match the BREF descriptors in the two images, and use Hamming distance vector<DMatch> matches; matcher->match(descriptors_1, descriptors_2, matches); //--Step 4: match point pair filtering // Calculate minimum distance and maximum distance auto min_max = minmax_element(matches.begin(), matches.end(), [](const DMatch &m1, const DMatch &m2) { return m1.distance < m2.distance; }); double min_dist = min_max.first->distance; double max_dist = min_max.second->distance; //When the distance between descriptors is more than twice the minimum distance, it is considered that the matching is wrong. But sometimes the minimum distance is very small, and an empirical value of 30 is set as the lower limit vector<DMatch> good_matches; int i; for ( i = 0; i < descriptors_1.rows; i++) { if (matches[i].distance <= max(2 * min_dist, 30.0)) { good_matches.push_back(matches[i]); } } //Save coordinate correspondence of matching point pair Vector4d point; for (i = 0; i < good_matches.size(); i++){ point << int(keypoints_1[good_matches[i].queryIdx].pt.x), int(keypoints_1[good_matches[i].queryIdx].pt.y), int(keypoints_2[good_matches[i].trainIdx].pt.x), int(keypoints_2[good_matches[i].trainIdx].pt.y); points.push_back(point); } return points; }
4. 3D point set acquisition
Through the third step of feature matching, we get the coordinates (u,v)(u,v)(u,v) of the matching point, but this is not a three-dimensional coordinate, so we need to convert it to the camera coordinate system, and then use the following formula,
[XYZ]=fxbd[fx0cx0fycy001][uv1]
\left[
\begin{matrix}
X \\
Y \\
Z
\end{matrix}
\right]
=\frac{f_xb}{d}
\left[
\begin{matrix}
f_x & 0 & c_x \\
0 & f_y & c_y \\
0 & 0 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
u \\
v \\
1
\end{matrix}
\right]
⎣⎡XYZ⎦⎤=dfxb⎣⎡fx000fy0cxcy1⎦⎤⎣⎡uv1⎦⎤
ddd is the parallax in the second step.
5. RANSAC
Although in the process of feature matching, we exclude some mismatches through if (matches [i]. Distance < = max (2 * min_dist, 30.0)) {good_matches. Push_back (matches [i]);}, but there are any mismatches, so we need to completely exclude the mismatches through RANSAC. The algorithm process of RANSAC is shown in the figure below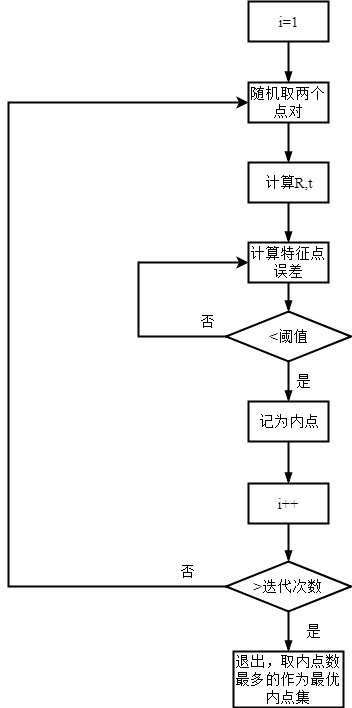
The code implementation is as follows:
double RANSAC_threshold, RANSAC_iterations; RANSAC_iterations = 1000;//Set the number of RANSAC iterations RANSAC_threshold = 0.1;//Set RANSAC threshold vector<Vector6d> inliers_best, inliers_current; int number_inliers_best = 0; Matrix3d matrix_R_best; Matrix<double, 3, 1> matrix_t_best; int k; for (k = 0; k < RANSAC_iterations; k++){ int number1,number2,number3,number4; number1 = rand() % pointscam.size(); number2 = rand() % pointscam.size(); number3 = rand() % pointscam.size(); number4 = rand() % pointscam.size(); Vector6d a,b,c,d; a = pointscam[number1]; b = pointscam[number2]; c = pointscam[number3]; d = pointscam[number4]; Matrix<double, 12, 12> matrix_A; matrix_A << a(0), a(1), a(2), 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, a(0), a(1), a(2), 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, a(0), a(1), a(2), 0, 0, 1, b(0), b(1), b(2), 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, b(0), b(1), b(2), 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, b(0), b(1), b(2), 0, 0, 1, c(0), c(1), c(2), 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, c(0), c(1), c(2), 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, c(0), c(1), c(2), 0, 0, 1, d(0), d(1), d(2), 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, d(0), d(1), d(2), 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, d(0), d(1), d(2), 0, 0, 1; Matrix<double, 12, 1> matrix_b; matrix_b << a(3), a(4), a(5), b(3), b(4), b(5), c(3), c(4), c(5), d(3), d(4), d(5); Matrix<double, 12, 1> x = matrix_A.colPivHouseholderQr().solve(matrix_b); Matrix3d matrix_R; matrix_R << x(0), x(1), x(2), x(3), x(4), x(5), x(6), x(7), x(8); Matrix<double, 3, 1> matrix_t; matrix_t << x(9), x(10), x(11); inliers_current.clear(); for (int i = 0; i < pointscam.size(); i++) { if (i == number1 || i == number2 || i == number3 || i == number4) continue; Vector3d delta_location; delta_location = Vector3d(pointscam[i](3), pointscam[i](4), pointscam[i](5)) - matrix_R * Vector3d(pointscam[i](0), pointscam[i](1), pointscam[i](2)) - matrix_t; double delta_location_norm; delta_location_norm = delta_location.norm(); if (delta_location_norm < RANSAC_threshold) { inliers_current.push_back(pointscam[i]); } } inliers_current.push_back(pointscam[number1]); inliers_current.push_back(pointscam[number2]); inliers_current.push_back(pointscam[number3]); inliers_current.push_back(pointscam[number4]); if (inliers_current.size() > number_inliers_best){ number_inliers_best = inliers_current.size(); inliers_best.clear(); inliers_best = inliers_current; matrix_R_best = matrix_R; matrix_t_best = matrix_t; } }
Among them, pointscan is vector < matrix < double, 6, 1 > > and records the matched 3D point set.
6. ICP estimation of pose
Here, we have obtained the matched 3D point set after RANSAC. Next, we use the ICP method based on SVD to estimate the pose, namely the rotation matrix RRR and the translation vector ttt. This part of code principle refers to section 7.9 3D-3D: ICP in Gao Xiang's vision SLAM 14 lectures.
int N = inliers_best.size(); Vector6d p; for (int i = 0; i < N; i++){ p += inliers_best[i]; } p = p / N;//Centroid of point set vector<Vector6d> q(N); for(int i = 0; i < N; i++){ q[i] = inliers_best[i] - p;//De centroid coordinates } Matrix3d W ; for (int i = 0; i < N; i++){ W += Vector3d( q[i](3), q[i](4), q[i](5) ) * Vector3d( q[i](0), q[i](1), q[i](2) ).transpose(); } cout << "W=" << endl; cout << W << endl; //Singular value decomposition of W Eigen::JacobiSVD<Eigen::Matrix3d> svd(W, Eigen::ComputeFullU | Eigen::ComputeFullV); Eigen::Matrix3d U = svd.matrixU(); Eigen::Matrix3d V = svd.matrixV(); Matrix3d R; R = U * V.transpose(); if (R.determinant() < 0) R = -R; Vector3d t; t = Vector3d( p(3), p(4), p(5) ) - R * Vector3d( p(0), p(1), p(2) ); cout << "from ICP Obtained rotation matrix R=\n" << R << endl; cout << "from ICP Resulting translation vector t=\n" << t << endl;
7. summary
Through the above 6 steps, we have realized a basic binocular vision odometer between two frames!
Outcome assessment
When the code is written, I use 000000.png-000600.png in the Odometry module 00 sequence in the KITTI data set to evaluate the effect. The result shows that the effect is too poor. Let's compare the true value of translation vector ttt: KITTI, the result value of VO between two frames of this binocular.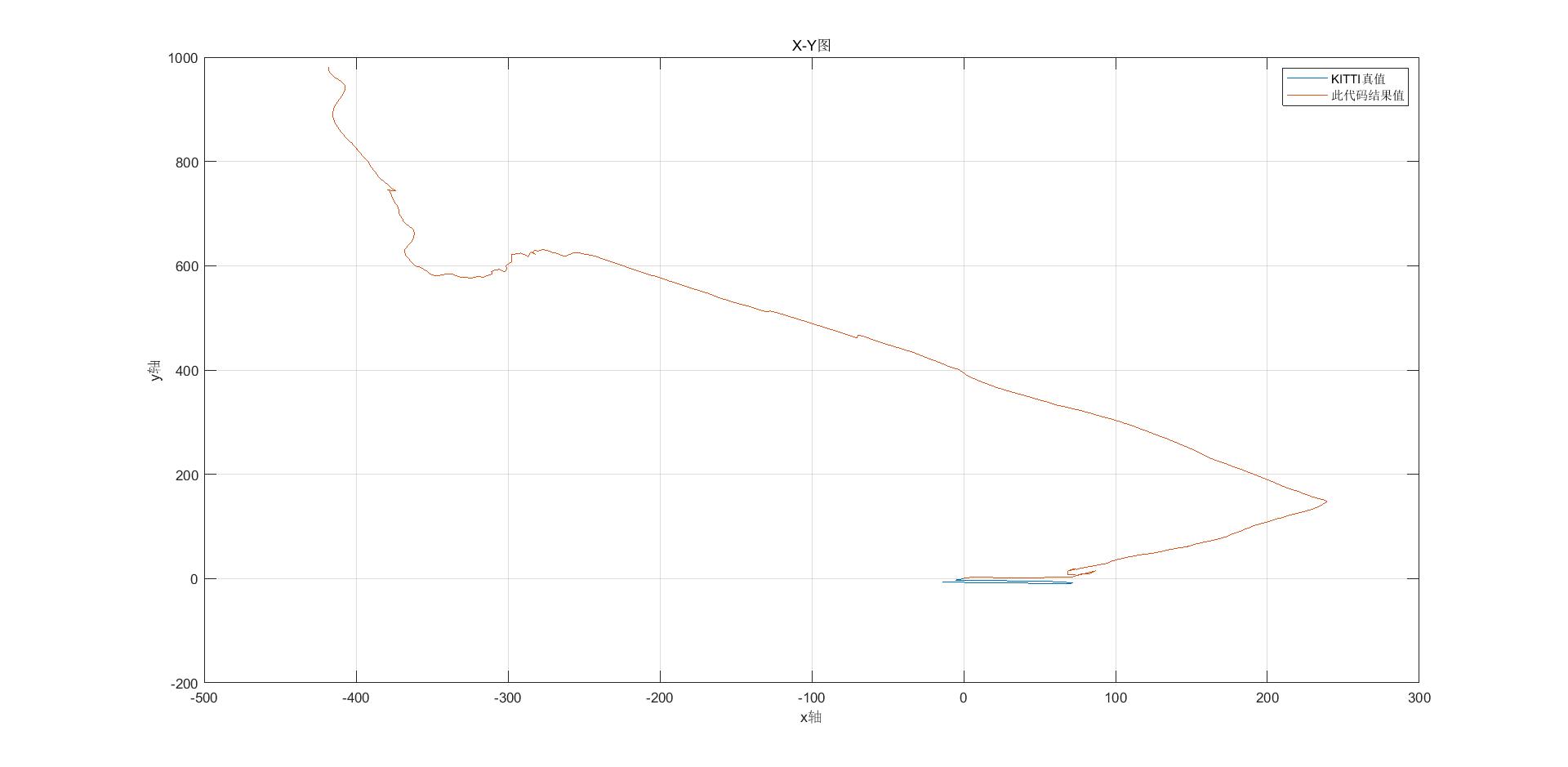
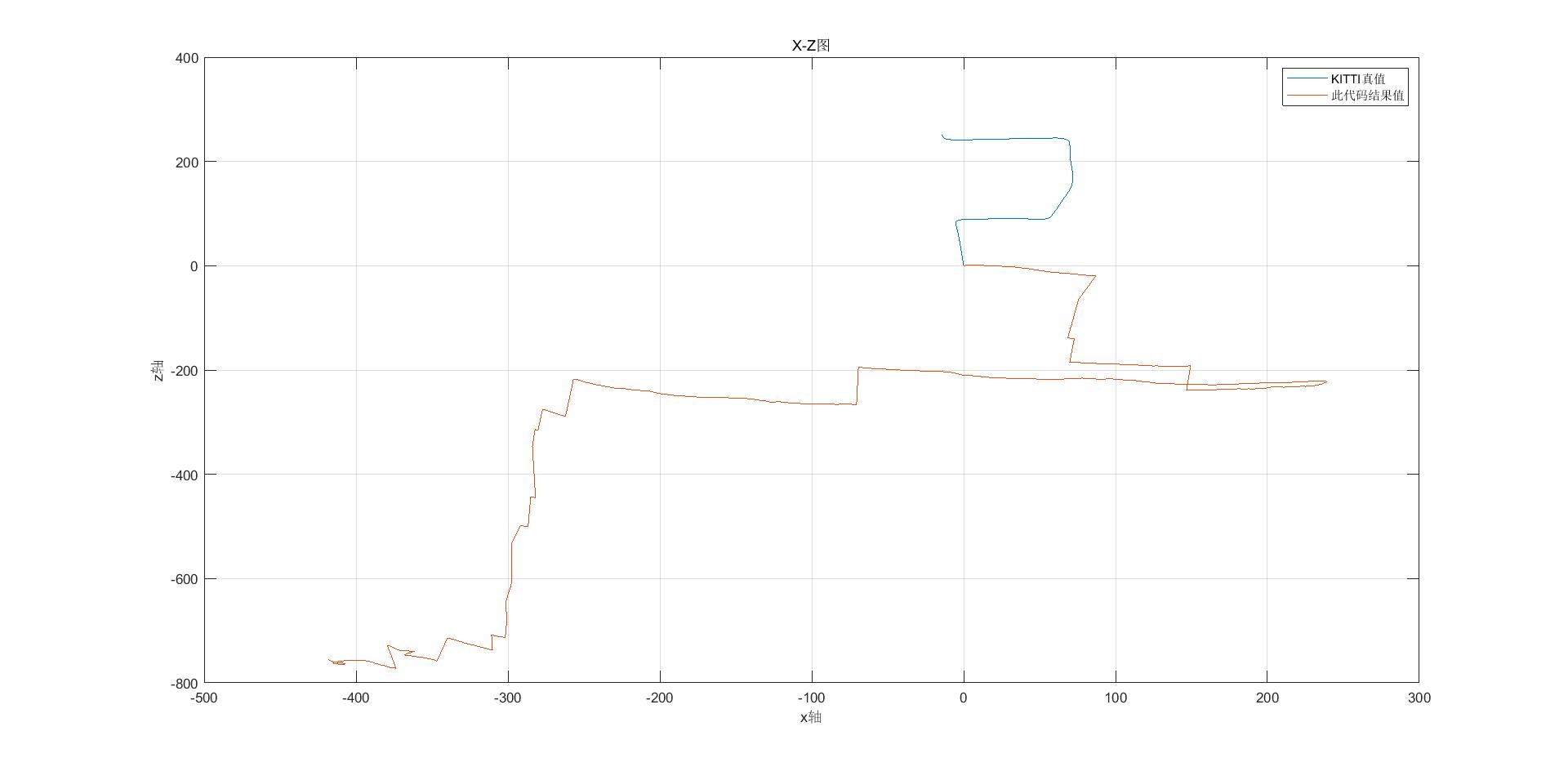

And the translation vector ttt value comparison of 000000.png-000010.png,
KITTI truth value
KITTI truth value
KITTI truth value
[−0.0469−0.0468−0.0469−0.0468−0.0469−0.0468−0.0469−0.0468−0.0469−0.0469−0.0284−0.0284−0.0284−0.0284−0.0284−0.0284−0.0284−0.0284−0.0284−0.02840.85870.85760.85870.85770.85870.85770.85880.85770.85860.8589]
\left[
\begin{matrix}
-0.0469 & -0.0468 & -0.0469 & -0.0468 & -0.0469 & -0.0468 & -0.0469 & -0.0468 & -0.0469 & -0.0469 \\
-0.0284 & -0.0284 & -0.0284 & -0.0284 & -0.0284 & -0.0284 & -0.0284 & -0.0284 & -0.0284 & -0.0284 \\
0.8587 & 0.8576 & 0.8587 & 0.8577 & 0.8587 & 0.8577 & 0.8588 & 0.8577 & 0.8586 & 0.8589
\end{matrix}
\right]
⎣⎡−0.0469−0.02840.8587−0.0468−0.02840.8576−0.0469−0.02840.8587−0.0468−0.02840.8577−0.0469−0.02840.8587−0.0468−0.02840.8577−0.0469−0.02840.8588−0.0468−0.02840.8577−0.0469−0.02840.8586−0.0469−0.02840.8589⎦⎤
Each of these columns is a translation vector.
Result value of this code
Result value of this code
Result value of this code
[0.55710.99293.94904.96496.93778.24137.94468.91228.32879.11181.36090.15631.12310.0765−0.5173−0.5405−0.58200.74460.13490.4579−0.2270−0.70070.3834−0.26950.69081.23471.48822.95033.88963.7126]
\left[
\begin{matrix}
0.5571 & 0.9929 & 3.9490 & 4.9649 & 6.9377 & 8.2413 & 7.9446 & 8.9122 & 8.3287 & 9.1118 \\
1.3609 & 0.1563 & 1.1231 & 0.0765 & -0.5173 & -0.5405 & -0.5820 & 0.7446 & 0.1349 & 0.4579 \\
-0.2270 & -0.7007 & 0.3834 & -0.2695 & 0.6908 & 1.2347 & 1.4882 & 2.9503 & 3.8896 & 3.7126
\end{matrix}
\right]
⎣⎡0.55711.3609−0.22700.99290.1563−0.70073.94901.12310.38344.96490.0765−0.26956.9377−0.51730.69088.2413−0.54051.23477.9446−0.58201.48828.91220.74462.95038.32870.13493.88969.11180.45793.7126⎦⎤
From the above results, we can see that the translation matrix ttt result obtained by this code is too bad, but what is the reason? Although I didn't add back-end optimization, mapping and loopback detection, shouldn't I have biased the results in the first place? Why?

