Related concepts

tree

(1) Tree: tree is a recursively defined data structure and an important non-linear data structure. A tree can be an empty tree without any nodes, or a non empty tree with at least one node.

(2) Root: a non empty tree with only one node. That node is the root.

(3) Subtree: in a non empty tree, all nodes except root can be divided into m (m ≥ 0) disjoint sets. Each set itself is a tree, called the root subtree.

(4) Node: represents the elements in the tree and some branches pointing to its subtree.

(5) Degree of a node: the number of subtrees owned by a node is called the degree of the node.

(6) Leaf: a node with a degree of 0.

(7) Child: the root of the node tree is called the child of the node.

(8) Parents: the upper node of a child's node is called the parents of the node.

(9) Sibling: a child of the same parents.

(10) Degree of tree: the maximum degree of nodes in a tree.

(11) Level of node: define the root as the first level from the root node, its child as the second level, and so on.

(12) Depth: the value of the maximum level of nodes in the tree.

(13) Ordered tree: the ordered tree refers to the one in which all the subtrees are ordered from left to right.

(14) Disordered tree: the disordered trees in the tree are called disordered trees.

(15) Forest is a collection of M (m ≥ 0) disjoint trees.

(16) Ancestor: refers to all nodes from the root node to this node.

Two fork tree

1. concept

(1) Each node has at most two subtrees, that is, there is no node with degree greater than 2 in the binary tree. The subtrees of a binary tree can be divided into left and right ones. The order of the left and right children cannot be reversed.

(2) There are five forms of binary trees:

(1) Empty binary tree.
(2) There is only one root node.
(3) There are only root nodes and left subtrees.
(4) There are only root nodes and right subtrees.
(5) There are root nodes and left and right subtrees.

(3) Full binary tree
A binary tree with a depth of K and 2k-1 nodes is called a full binary tree

(4) Complete binary tree
If there is a binary tree with depth k and n nodes, it is called a complete binary tree if and only if each node corresponds to the nodes numbered from 1 to n in the full binary tree with depth k.

(5) Binary search tree

• Each node contains a key, also known as the data field of data
• When the left subtree is not empty, each node value of the left subtree is smaller than the value of the root node, that is, l < p
• When the right subtree is not empty, each node value of the right subtree is greater than the value of the root node, that is, P < R
• Duplicate values are not allowed for nodes
• The left and right subtrees of any node conform to the above rules
• Middle order traversal can make nodes ordered
• The left and right subtrees of any node are also binary search trees
  

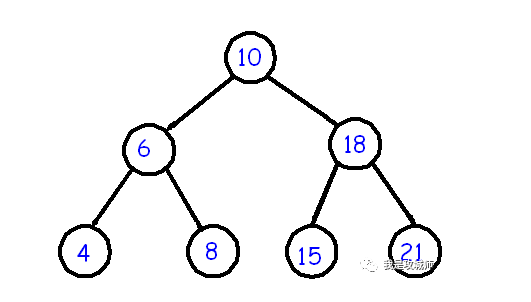
2. nature

(1) There are at most 2i-1(i ≥ 1) on the i-th layer of a binary tree.

(2) A binary tree with a depth of K has at most 2k-1 nodes (K ≥ 1).

(3) For any binary tree, if n0, n1 and n2 represent node trees with degrees of 0, 1 and 2 respectively, then n0=n2+1.

(4) The depth of a complete binary tree with n nodes is log2n + 1.

(5) For a complete binary tree with n nodes, for any node i (1 ≤ I ≤ n), there are:

• If i=1, then node I is the root node of the binary tree, without parents; if I > 1, then PARENT(i) is node i/2.
• If 2i > N, node i has no left child (node I is leaf node); otherwise, its left child LCHILD(i) node 2i.
• If 2i+1 > N, node i has no right child; otherwise, its right child RCHILD(i) is node 2i+1.

3. storage

(1) Sequential storage structure

The sequential storage structure is only suitable for the storage of complete binary tree, that is to store the complete binary tree from top to bottom and from left to right in a continuous storage space. Generally stored in one-dimensional array.

The sequence storage structure of the complete binary tree in the above figure is as follows:

(2) Chain storage structure

The chain storage structure has two fork linked list structure and three fork linked list storage structure. Generally, binary list is used for storage.
The node structure of binary list is defined as follows:

typedef struct bitnode
{
	int num;
	struct bitnode *lchild;
	struct bitnode *rchild;
}TreeNode;

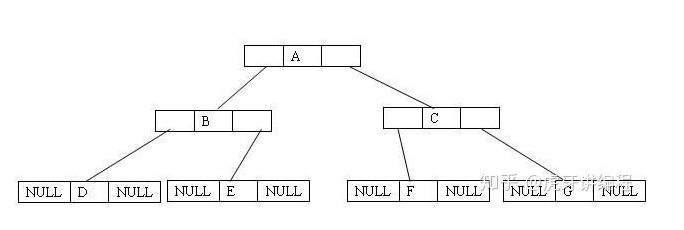
4. traversal

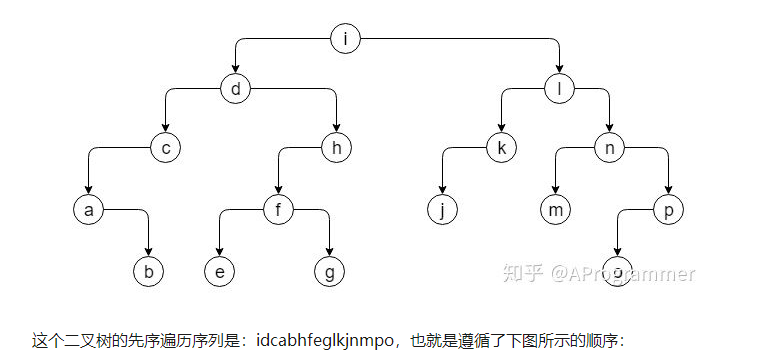
There are three ways of traversing binary tree: pre order traversal, middle order traversal and post order traversal

(1) Implementation of preamble traversal code

Recursive implementation

struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};
//Recursive implementation of preorder traversal
void travPre_R(TreeNode* pRoot)
{
    if(pRoot==NULL)//The condition for the end of recursion is that the node is empty
        return;
    cout<<pRoot->val;//Output root
    travPre_R(pRoot->left);//Traverse left subtree
    travPre_R(pRoot->right);//Traversal right subtree
}

Iterative implementation

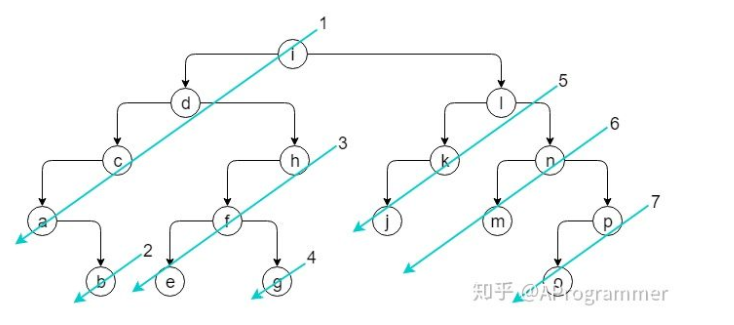
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};

//Create a function to access the nodes on the left chain of the binary tree, starting from the current node and going further along the left branch
void visitAlongLeftBranch(TreeNode* pRoot,stack<TreeNode*>& s)
{
    while(pRoot)
    {
        cout<<pRoot->val;//Access current node
        if(pRoot->right)//If there is a right node, first stack the right node
            s.push(pRoot->right);
        pRoot=pRoot->left;//Drill down left branch
    }
}

//Functions of traversal of preorder by iteration
void travPre_l(TreeNode* pRoot)
{
    stack<TreeNode*> s;//Create an auxiliary stack to store the right node
    while(true)
    {
        visitAlongLeftBranch(pRoot,s);//Starting from the current node, visit the left node from top to bottom
        if(s.empty())//The stack is empty, indicating that all nodes have been accessed, ending the cycle
            break;
        pRoot=s.pop();//Pop up start of next batch
    }
}

(2) Middle order ergodic

Recursive implementation:

struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};
//Recursive implementation of middle order traversal
void travPre_R(TreeNode* pRoot)
{
    if(pRoot==NULL)//The condition for the end of recursion is that the node is empty
        return;
    travPre_R(pRoot->left);//Traverse left subtree
    cout<<pRoot->val;//Output root
    travPre_R(pRoot->right);//Traversal right subtree

}

Iterative implementation:

//Create a function to start from the current node and continue to deepen along the left branch until there is no node with left branch
void goAlongLeftBranch(TreeNode* pRoot,stack<TreeNode*>& s)
{
    while(pRoot)
    {
        s.push(pRoot);//Stack the current node
        pRoot=pRoot->left;//Drill down the left branch and iterate until there is no left child
    }
}

//Functions of middle order traversal by iteration
void travIn_l(TreeNode* pRoot)
{
    stack<TreeNode*> s;//Create an auxiliary stack to store the right node
    while(true)
    {
        goAlongLeftBranch(pRoot,s);//Starting from the current node, stack the left node in sequence from top to bottom
        if(s.empty())//The stack is empty, indicating that all nodes have been accessed, ending the cycle
            break;
        pRoot=s.pop();//pRoot is the lowest node on the left chain
        cout<<pRoot->val;
        pRoot=pRoot->right;//Visit its right subtree again
    }
}

(3) Postorder ergodic

Recursive implementation

//Recursive implementation of post order traversal
void travPre_R(TreeNode* pRoot)
{
    if(pRoot==NULL)//The condition for the end of recursion is that the node is empty
        return;
    travPre_R(pRoot->left);//Traverse left subtree
    travPre_R(pRoot->right);//Traversal right subtree
    cout<<pRoot->val;//Output root

}

Exercise 1: rebuilding a binary tree

Enter the results of the preorder traversal and inorder traversal of a binary tree, and rebuild the binary tree. It is assumed that the results of the input preorder traversal and preorder traversal do not contain duplicate numbers. For example, if the sequence {1,2,4,7,3,5,6,8} and the sequence {4,7,2,1,5,3,8,6} are input, the binary tree will be reconstructed and returned.

Principle and train of thought

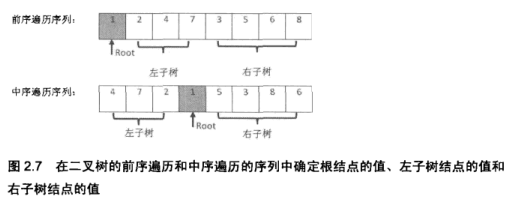
Method steps

1. The first element pre[0] of preorder traversal is the value of the root node. According to the value of the root node, find the location gen of the root node in the preorder traversal
2. Left subtree:
(1) Use VIN left to store the middle order traversal sequence of left subtree, and save vin[0]-vin[gen-1] to VIN left in turn (use vector's push back function)
(2) Pre left is used to store the pre traversal sequence of left subtree, and pre[1]-pre[gen] is stored in pre left in turn (i+1 is because pre[0] is the root node, and pre left is stored from pre[1])
3. Right subtree:
(1) In this paper, vin[gen+1]-vin[len-1] is successively stored in VIN [u right [i]
(2) Pre right [i] is used to store the traversal sequence of the right subtree, and vin[gen+1]-vin[len-1] is successively stored in pre right [i]
4. Recursion: reconstruct left and right subtrees respectively according to the same method until the leaf node, i.e. until the length of the new traversal sequence is 0 (so it is necessary to judge whether the length len of the traversal sequence is 0 at the beginning)
5. Return to the root node.

Code

/**
 * Definition for binary tree
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin) {
        int len=vin.size();//Length of traversal sequence
        if (len==0)
            return NULL;
        TreeNode *root=new TreeNode(pre[0]);//A new node is defined to represent the root node. The value of the root node is the first element traversed in the previous order

        vector<int> pre_left,pre_right,vin_left,vin_right;//Store the left and right subtrees of preorder traversal and middle order traversal respectively
        
        //Find the location of root node in middle order traversal
        int gen=0;//gen represents the location of the root node
        for (int i = 0; i < len; ++i)
        {
            if (vin[i]==pre[0])
            {
                gen=i;
                break;
            }
        }
        //Left tree
        for (int i = 0; i < gen; ++i)
        {
            vin_left.push_back(vin[i]);//The middle order traversal elements of the left subtree are successively stored in VIN? Left
            pre_left.push_back(pre[i+1]);
        }
        //Right subtree
        for (int i = gen+1; i < len; ++i)
        {
            vin_right.push_back(vin[i]);
            pre_right.push_back(pre[i]);
        }
        root->left=reConstructBinaryTree(pre_left,vin_left);
        root->right=reConstructBinaryTree(pre_right,vin_right);
        return root;
    }
};

Exercise 2: the substructure of the tree

Input two binary trees a and B to determine whether B is a substructure of A. (ps: we agree that an empty tree is not a substructure of any tree)

Sword finger offer (10) -- robustness of code

Exercise 3: binary tree mirroring

Operate the given binary tree and transform it into a mirror image of the source binary tree.

Sword finger offer (11) -- drawing to visualize abstract problems

Exercise 4: print the binary tree from top to bottom

Each node of the binary tree is printed from top to bottom, and the nodes of the same layer are printed from left to right.
Sword finger offer (12) -- concrete abstract problems with examples

Exercise 5: post order traversal sequence of binary search tree

Input an integer array to determine whether the array is the result of the subsequent traversal of a binary search tree. If Yes, output Yes; otherwise, output No. Suppose that any two numbers of the input array are different from each other.
Sword finger offer (12) -- concrete abstract problems with examples

Exercise 6: the path of a value in a binary tree

Input the root node and an integer of a binary tree, and print out all paths whose sum of node values in the binary tree is the input integer. Path is defined as a path from the root node of the tree to the node that the leaf node passes through. (Note: in the list of returned values, the array with large array length is first)
Sword finger offer (12) -- concrete abstract problems with examples

Exercise 7: binary search tree and double linked list

Input a binary search tree, and transform the binary search tree into a sorted bidirectional linked list. It is required that no new node can be created, only the node pointer in the tree can be adjusted.

Sword finger offer (XIII) -- simplify complex problems by decomposition