First: Concepts
A binary search tree, also known as a binary sorting tree, is either an empty tree** or a binary tree with the following properties:
If its left subtree is not empty, the values of all nodes in the left subtree are less than those of the root node.
If its right subtree is not empty, the values of all nodes in the right subtree are greater than those of the root node.
Its left and right subtrees are also binary search trees.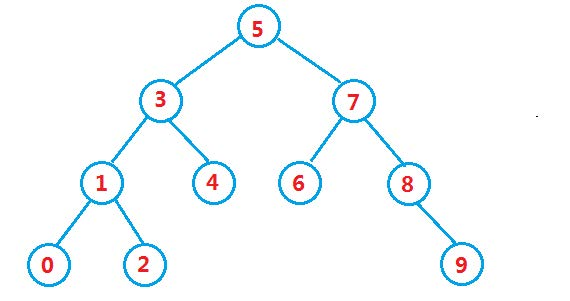

2: Operation - Find
Compare with the root node first, return equally, if not,
Key>root node key, find in right subtree (root=root.rightChild)
Key<root node key, find in left subtree (root=root.leftChild)
Otherwise return false

Three: Operation - Insert
According to the nature of the binary sort tree, the left child has a smaller value than the root node and the right child has a larger value than the root node.The key of a key is compared before the key of the root node, and then the left or right comparison with the key of the root node is determined to satisfy the properties of the binary sorting tree, which is a reasonable position, and then inserted.

Operation-Delete (Difficulty)
Set the node to be deleted to cur and the parent node to be deleted to parent
1. cur.left == null

1. Cur is root, then root = cur.right
2. Cur is not root, cur is parent.left, parent.left = cur.right
3. Cur is not root, cur is parent.right, parent.right = cur.right
   2. cur.right == null
4. Cur is root, then root = cur.left
5. Cur is not root, cur is parent.left, parent.left = cur.left
6. Cur is not root, cur is parent.right, parent.right = cur.left
   3. cur.left != null && cur.right != null
7. Need to delete by substitution, that is, find the first node in the middle order in its right subtree (the smallest key code), fill the deleted node with its value, and then deal with the deletion of the node.

Five: Realization

public class BinarySearchTree<K extends Comparable<K>, V>
{ 
public static class Node<K extends Comparable<K>, V> 
{
K key; 
V value; 
Node<K, V> left;
Node<K, V> right;

public String toString()
{ 
return String.format("{%s, %s}", key, value);
}
}
private Node<K, V> root = null;
public V get(K key) 
{ 
Node<K, V> parent = null; 
Node<K, V> cur = root; 
while (cur != null)
{ 
parent = cur;
int r = key.compareTo(cur.key);
if (r == 0)
{ 
return cur.value;
} 
else if (r < 0) {
cur = cur.left; 
}

else 
{
cur = cur.right;
} 
}
return null; 
}
public V put(K key, V value)

{ 
if (root == null)
{ root = new Node<>();
root.key = key;
root.v
display(root);
return null;
}
Node<K, V> parent = null; 
Node<K, V> cur = root; 
while (cur != null) 
{ 
parent = cur;

int r = key.compareTo(cur.key);
if (r == 0) 
{ 
V oldValue = cur.value; 
cur.value = value; 
display(root); 
return oldValue; 
}
else if (r < 0)
{ 
cur = cur.left; 
} 
else

{ 
cur = cur.right;
} 
}
Node<K, V> node = new Node<>(); 
node.key = key; 
node.value = value;
int r = key.compareTo(parent.key);
if (r < 0)
{ parent.left = node;
} 
else { parent.right = node; 
}
display(root); 
return null; 
}
public V remove(K key) 
{ 

Node<K, V> parent = null; 
Node<K, V> cur = root; 
while (cur != null) 
{ 
int r = key.compareTo(cur.key);
if (r == 0)
{ 
V oldValue = cur.value; 
deleteNode(parent, cur);
display(root); 
return oldValue; } 
else if (r < 0)
{ parent = cur; cur = cur.left; }
else { parent = cur; cur = cur.right; 
} 
}
display(root); 
return null;
}
private void deleteNode(Node<K,V> parent, Node<K,V> cur) 
{
if (cur.left == null)
{
if (cur == root)
{
root = cur.right;
} 
else if (cur == parent.left)
{ parent.left = cur.right; }
else { parent.right = cur.right; }
} else if (cur.right == null)
{ 
if (cur == root)
{ root = cur.left; }
else if (cur == parent.left)
{ parent.left = cur.left; }
else { parent.right = cur.left; }
} else {
// Find the node scapegoat with the smallest key in the right subtree of cur
// That is, the node scapegoat.left == null
Node<K,V> goatParent = cur;
Node<K,V> scapegoat = cur.right;
while (scapegoat.left != null)
{ goatParent = scapegoat; scapegoat = cur.left; }
cur.key = scapegoat.key;
cur.value = scapegoat.value;
if (scapegoat == goatParent.left)
{
goatParent.left = scapegoat.right;
}
else { goatParent.right = scapegoat.right; }
} 
}
private static <K extends Comparable<K>,V> void display(Node<K,V> node) 
{
System.out.print("Preorder: ");
preOrder(node);

System.out.println();
System.out.print("Middle Order: ")
inOrder(node); 
System.out.println(); }
private static <K extends Comparable<K>,V> void preOrder(Node<K,V> node)
{ if (node == null)
{ return; }
System.out.print(node + " ");
preOrder(node.left);
preOrder(node.right); }
private static <K extends Comparable<K>,V> void inOrder(Node<K,V> node)
{ if (node == null) 
{ return; }
inOrder(node.left);
System.out.print(node + " ");
inOrder(node.right); }
public static void main(String[] args)
{ 
BinarySearchTree<Integer, String> tree = new BinarySearchTree<>(); 
int[] keys = { 5, 3, 7, 4, 2, 6, 1, 9, 8 }; 
for (int key : keys) 
{
tree.put(key, String.valueOf(key)); }
System.out.println("=================================="); tree.put(3, "Modified 3"); System.out.println("=================================="); tree.remove(9);
tree.remove(1); t
ree.remove(3);
``` } 
}

**6: Performance Analysis**
Both insert and delete operations must be searched first, and the efficiency of the search represents the performance of each operation in the binary search tree.
For binary search trees with n nodes, if the probability of finding each element is equal, the average search length of the binary search tree is a function of the depth of the nodes in the binary search tree, that is, the deeper the nodes are, the more comparisons occur.
However, for the same set of keycodes, if the order of insertion is different, different binary search trees may be obtained.
**7: Relationship to the java class set**
TreeMap and TreeSet are Maps and Sets implemented in java using search trees;