Basic operations of binary tree construction, traversal, transformation to generalized table, etc
I. structure definition
The binary tree can be divided into two parts: node and edge, which is the same as graph, in which node represents event, then edge represents the relationship between events.
in addition, each node can be regarded as the union of its left and right child nodes; in other words, if the left and right child nodes of a node are combined, then the union can represent this node; therefore, it is not difficult for us to find that the tree data structure corresponds to a series of complete inclusion relations (which is very important).
? That is the stack!!!
Let's first implement the structure definition of binary tree
typedef struct Node { //Including data field and left and right child pointer fields char data; struct Node *lchild, *rchild; } Node;
Construction of binary tree
- We know that there are three kinds of traversal order of binary tree: first, middle and last. In the first, middle and last three kinds of traversal order of binary tree, if we know middle order traversal + front order traversal, or middle order traversal + back order traversal, we can uniquely determine a binary tree (front order + back order No), so given any of our two sequence collocations, we can build the binary tree we want.
The implementation code is as follows:
Node *getNewNode(char val) { //Generate a binary tree node according to the passed value Node *node = (Node *)malloc(sizeof(Node)); node->data = val; node->lchild = node->rchild = NULL; return node; } //Parameters: the string of the sequence traversed in the first and middle order, and the length len of the string //Return value: returns the root node of the constructed binary tree Node *build(char *pre_str, char *in_str, int len) { Node *root = getNewNode(pre_str[0]); //Create root node int ind = strchr(in_str, root->data) - in_str; //Get the subscript ind of root character in the middle order traversal sequence if (ind > 0) { //If the left subtree is not empty, recursively construct the left subtree root->lchild = build(pre_str + 1, in_str, ind); } if (len - ind - 1 > 0) { //If the right subtree is not empty, recursively construct the right subtree root->rchild = build(pre_str + ind + 1, in_str + ind + 1, len - ind - 1); } return root; }
- In addition to building a binary tree by using pre order + middle order and post order + middle order, we usually build a binary tree according to the generalized table corresponding to the binary tree (each generalized table corresponds to a binary tree uniquely). For what is a generalized table, please look down:
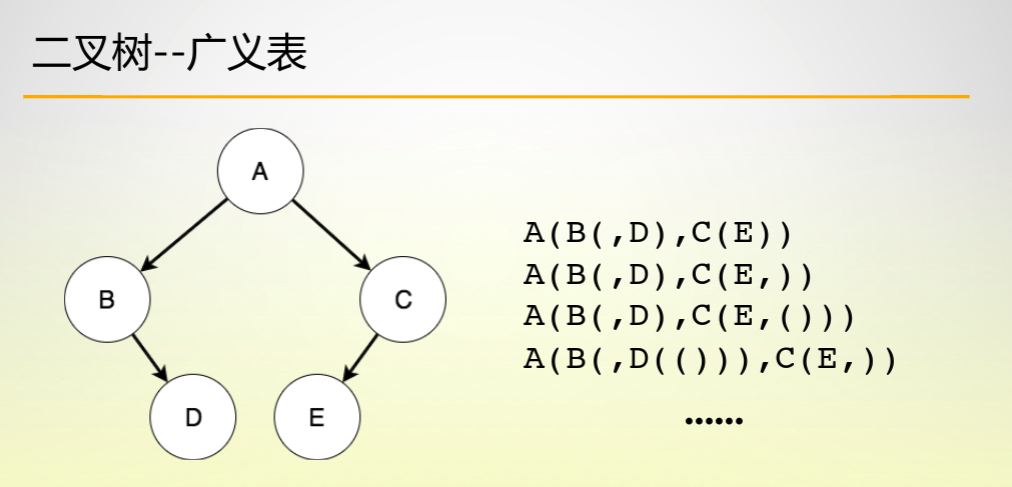
As shown in the figure: the above binary tree has four kinds of generalized table representations on the right. The author prefers the second one. Next, we will implement the code:
//Parameter: the character array corresponding to the generalized table. node_num is the incoming parameter, which is used to get the number of nodes in the tree //Return value: returns the root node of the constructed binary tree Node *build(char *str, int *node_num) { Node *tmp = NULL, *top_p = NULL; int flag = 0; stack<Node *> s; while (str[0]) { //Traversal generalized table string switch (str[0]) { case '(': { //Left parenthesis encountered flag = 0; s.push(tmp); tmp = NULL; break; } case ')': { //Right parenthesis encountered top_p = s.top(); s.pop(); break; } case ',': { //Encounter comma flag = 1; tmp = NULL; break; } case ' ': { //Encounter spaces break; } default: { //Encounter letters tmp = getNewNode(str[0]); //Create node if (!s.empty() && !flag) { s.top()->lchild = tmp; } else if (!s.empty() && flag) { s.top()->rchild = tmp; } (*node_num)++; //Number of nodes plus one } } str++; //str pointer backward } if (tmp && !top_p) top_p = tmp; return top_p; }
I think you are confused when you see the code (also in the beginning). Don't worry. Let's start with bracket matching.
the specific method is: when we encounter the left bracket, put the bracket into the stack. When we encounter the right bracket, check the top element of the stack to see whether it is the corresponding left bracket. If it does not match, directly return false, indicating that the overall bracket does not match. If it matches, pop up the top element of the stack, and then repeat the string. When we traverse the string, if the stack is not empty at this time, then return false, if the stack is Null, return true, indicating bracket matching.
? Bracket matching is an event complete inclusion problem. Similarly, we said at the beginning of the article that the relationship between the parent and child nodes in a binary tree is a union relationship, and this parent node may be a child of other nodes at the same time. Therefore, the construction of a binary tree is the same event complete inclusion problem, which we can also use stack to achieve!!!
when we first encounter a character, we put it on the stack; when we meet the left bracket, we know that the next character is the left child of the previous character (in order to judge whether the next character is the left child or the right child of the stack top element, we set a flag as flag, flag = 0 for the left child, flag = 0 for the left child= 1 is the right child), so we set the flag to 0 and put the previous characters in the stack. When we meet the characters corresponding to the left child, we generate a node and point the left child pointer of the top element of the stack to the node. When we meet the comma, we know that the next character is the right child, so we set the flag to 1. When we meet the space, we don't need to deal with it (the reason why spaces are judged here is to prevent users from entering spaces). In this way, we can get the corresponding binary tree of the generalized table.
Four traversal methods of three binary tree: front middle back and depth first
The first, middle and last three kinds of order are relative to the order of the root node. I believe you all know these three kinds of traversal methods very well. I will not repeat them here, but show the code directly. In addition, Xiaobian also wants to make a long statement. The nodes in the tree can be regarded as fruits of each tree, which can be directly dropped to get the middle order sequence. As for width first traversal, it needs to be realized with data structure such as queue.
void pre_order(Node *root, vector<char>& v) { //Preorder traversal, saving the result in the vector v if (!root) return ; v.push_back(root->data); pre_order(root->lchild, v); pre_order(root->rchild, v); } void in_order(Node *root, vector<char>& v) { //Sequential traversal if (!root) return ; in_order(root->lchild, v); v.push_back(root->data); in_order(root->rchild, v); } void post_order(Node *root, vector<char>& v) { //Post order traversal if (!root) return ; post_order(root->lchild, v); post_order(root->rchild, v); v.push_back(root->data); } void BFS(Node *root, vector<char>& v) { //Depth first traversal, queue required if (!root) return ; queue<Node *> q; q.push(root); while (!q.empty()) { Node *tmp = q.front(); v.push_back(tmp->data); q.pop(); if (tmp->lchild) q.push(tmp->lchild); if (tmp->rchild) q.push(tmp->rchild); } }
Quad binary tree to generalized table
Similarly, the code is shown as follows:
void tree_to_table(Node *root) { if (!root) return ; printf("%c", root->data); if (root->lchild == NULL && root->rchild == NULL) return ; printf("("); tree_to_table(root->lchild); printf(","); tree_to_table(root->rchild); printf(")"); }
I want to insert a sentence here, that is, in the tree, most of the code is implemented by recursion, so if recursion is not learned, the tree part will be very difficult
V. other operations
int get_node_num(Node *root) { //Get the number of nodes in the tree if (!root) return 0; return get_node_num(root->lchild) + get_node_num(root->rchild) + 1; } int get_tree_depth(Node *root) { //Get the height of the tree if (!root) return 0; int n = 0, m = 0; m = get_tree_depth(root->rchild); return max(n, m) + 1; } int get_leaf_num(Node *root) { //Get the number of leaf nodes if (!root) return 0; if (root->lchild == NULL && root->rchild == NULL) return 1; return get_leaf_num(root->lchild) + get_leaf_num(root->rchild); } void printAllPath(Node *T,char path[],int pathDepth){ //Print the path from all leaf nodes to root nodes if(T != NULL){ path[pathDepth] = T->data; if(T->lchild == NULL && T->rchild == NULL){ for(int i = pathDepth; i >= 0; i--) cout << path[i] << " "; cout << endl; }else{ printAllPath(T->lchild,path,pathDepth + 1); printAllPath(T->rchild,path,pathDepth + 1); } } }
Finally, as for the properties of binary tree, Xiaobian doesn't want to elaborate too much here. You can search directly online, only a little. Xiaobian thinks it's very important. It's necessary to explain to you: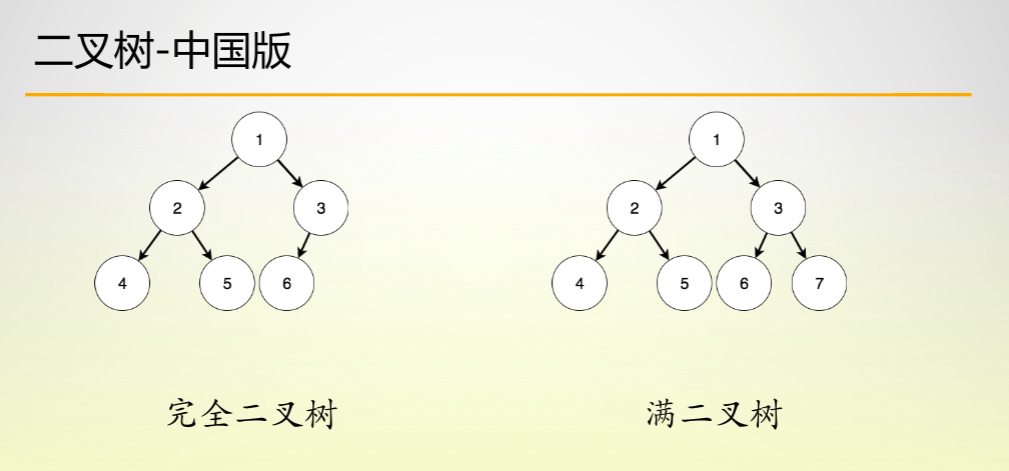
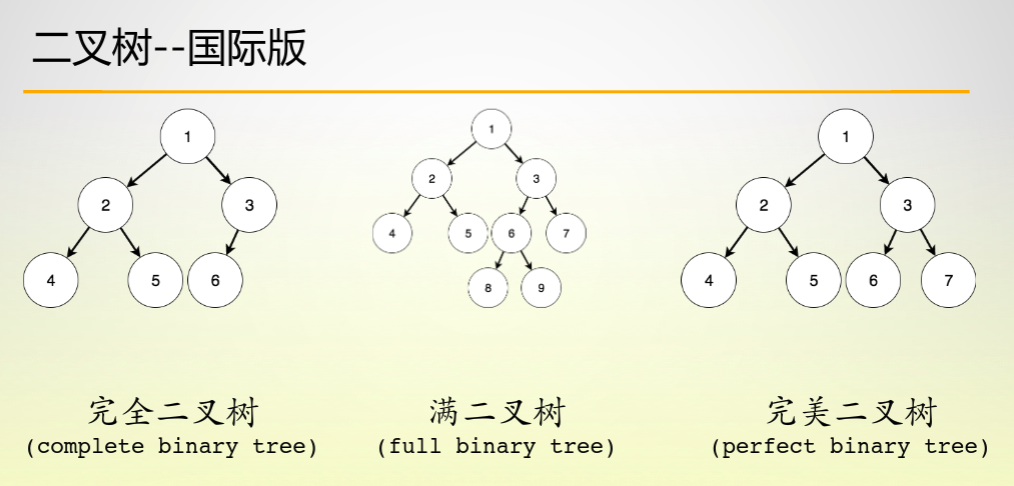
In the course of data structure of University, the definitions of complete binary tree and full binary tree are all adopted in Chinese version. However, for the small partners who want to go abroad, they must understand the differences between perfect binary tree, full binary tree and perfect binary tree and their quasi definiteness.
Finally: total code:
#include <iostream> #include <stack> #include <vector> #include <queue> using namespace std; typedef struct Node { char data; struct Node *lchild, *rchild; } Node; Node *getNewNode(char val) { Node *node = (Node *)malloc(sizeof(Node)); node->data = val; node->lchild = node->rchild = NULL; return node; } Node *build(char *str, int *node_num) { //Tree based on string, return root node Node *tmp = NULL, *top_p = NULL; int flag = 0; stack<Node *> s; while (str[0]) { switch (str[0]) { case '(': { flag = 0; s.push(tmp); tmp = NULL; break; } case ')': { top_p = s.top(); s.pop(); break; } case ',': { flag = 1; tmp = NULL; break; } case ' ': { break; } default: { tmp = getNewNode(str[0]); if (!s.empty() && !flag) { s.top()->lchild = tmp; } else if (!s.empty() && flag) { s.top()->rchild = tmp; } (*node_num)++; } } str++; } if (tmp && !top_p) top_p = tmp; return top_p; } void in_order(Node *root, vector<char>& v) { if (!root) return ; in_order(root->lchild, v); v.push_back(root->data); in_order(root->rchild, v); } void BFS(Node *root, vector<char>& v) { if (!root) return ; queue<Node *> q; q.push(root); while (!q.empty()) { Node *tmp = q.front(); v.push_back(tmp->data); q.pop(); if (tmp->lchild) q.push(tmp->lchild); if (tmp->rchild) q.push(tmp->rchild); } } void tree_to_table(Node *root) { if (!root) return ; printf("%c", root->data); if (root->lchild == NULL && root->rchild == NULL) return ; printf("("); tree_to_table(root->lchild); printf(","); tree_to_table(root->rchild); printf(")"); } int get_node_num(Node *root) { if (!root) return 0; return get_node_num(root->lchild) + get_node_num(root->rchild) + 1; } int get_tree_depth(Node *root) { if (!root) return 0; int n = 0, m = 0; m = get_tree_depth(root->rchild); return max(n, m) + 1; } int get_leaf_num(Node *root) { if (!root) return 0; if (root->lchild == NULL && root->rchild == NULL) return 1; return get_leaf_num(root->lchild) + get_leaf_num(root->rchild); } void clear(Node *root) { if (!root) return ; clear(root->lchild); clear(root->rchild); free(root); } int main() { char str[100] = {0}; scanf("%[^\n]s", str); int node_num = 0; Node *root = build(str, &node_num); printf("node_num = %d\n", get_node_num(root)); vector<char> v; in_order(root, v); vector<char>::iterator it; printf("in_order: ["); for (it = v.begin(); it != v.end(); it++) { if (it != v.begin()) printf(" "); printf("%c", *it); } printf("]\n"); printf("tree_to_table: "); tree_to_table(root); printf("\n"); printf("tree's depth = %d\n", get_tree_depth(root)); printf("tree's leaf node number = %d\n", get_leaf_num(root)); vector<char> v2; BFS(root, v2); vector<char>::iterator it2; printf("BFS: ["); for (it2 = v2.begin(); it2 != v2.end(); it2++) { if (it2 != v2.begin()) printf(" "); printf("%c", *it2); } printf("]\n"); return 0; } /* Input: A(B(D,E),C(F,G)) Output: node_num = 7 in_order: [D B E A F C G] tree_to_table: A(B(D,E),C(F,G)) tree's depth = 3 tree's leaf node number = 4 BFS: [A B C D E F G] */
Digression
Come on! It's a long way to go. I'll go up and down
Tree is a very important part, refueling, refueling recursion!!

