14.1 hidden Markov model

HMM and Viterbi algorithm
Hidden Markov model predicts hidden sequence by given observation sequence. It is often used to mine hidden information from the surface information of sequence, such as speech recognition and handwriting recognition. In principle, HMM can also perform tasks such as part of speech tagging, Chinese word segmentation, etc., but because the height and width of confusion matrix are determined by the number of observation sequences, when it is applied to large corpus, the size of word set is often tens of thousands, so the confusion matrix needs to store hundreds of millions of parameters, which is disastrous for the computer, no matter how many times it runs or how much memory it occupies At the same time, a big assumption of the hidden Markov model is that the hidden state of the current time step is only related to the explicit state of the current time and the implicit state of the previous time, while the actual situation is that the meaning and annotation form of words are affected by multiple words in the context at the same time. Therefore, the hidden Markov model in this kind of NLP The task is eliminated rapidly, and the opportunity is transferred to conditional random airport and other models to break the time dependence hypothesis.

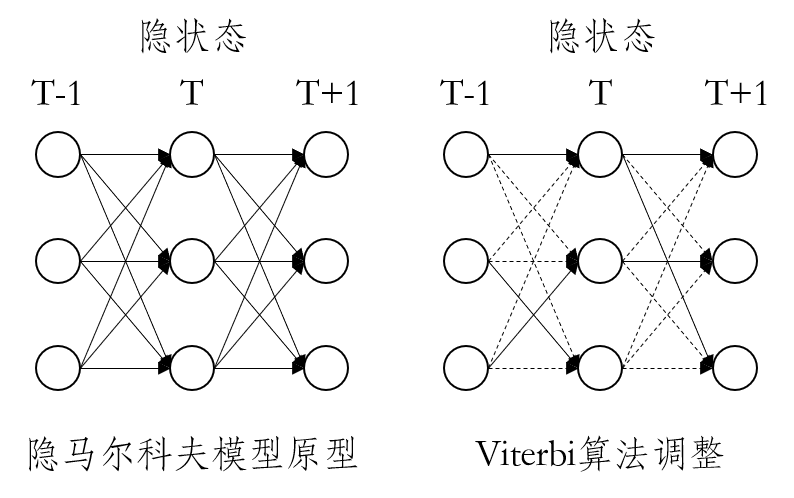
Viterbi algorithm is used to find the maximum probability path in the field of dynamic planning. In fact, the prediction of a certain type of hidden state in the current time step by hidden Markov model is based on the sum of all possibilities after the previous hidden state is transferred; Viterbi algorithm adjusts this idea, and only takes the path with the greatest probability after the previous hidden state is transferred. As shown in the figure below:

import numpy as np
class HMM(object):
    '''
    //Algorithm principle:
    	- train
    		//According to the principle of statistical conditional distribution, the edge distribution, transition matrix and confusion matrix of hidden state are generated
    	- Forecast
        	i.The global hidden state probability distribution is multiplied by the column corresponding to the obvious state in the confusion matrix to predict the hidden state distribution at the initial time
        	ii.Enter the next time step, multiply the hidden state distribution of the previous time by the transition matrix
        	iii.The results of the multiplication are multiplied by the columns corresponding to the apparent state of the time in the confusion matrix to predict the distribution of the hidden state of the time
        	iii.Cycle number 1 ii,iii step.
    	- Forecast(Viterbi)
        	i.The global hidden state probability distribution is multiplied by the column corresponding to the obvious state in the confusion matrix to predict the hidden state distribution at the initial time
        	ii.Enter the next time step, multiply the hidden state distribution of the previous time by the elements in the transition matrix, and take the maximum value
        	iii.The maximum probability sequence is multiplied by the column corresponding to the explicit state in the confusion matrix to predict the implicit state distribution at that time
        	iii.Cycle number 1 ii,iii step.
    '''
    def __init__(self):
        self.train = None    #Training set display state sequence
        self.label = None    #Training set hidden state sequence
        self.prob = None    #Global hidden state edge distribution
        self.trans = None    #Transition matrix (row: hidden state at time t col: hidden state at time t + 1)
        self.emit = None    #Emission (confusion) matrix (row: hidden state col: explicit state)
    def fit(self,train,label):
        '''The training set is imported to generate the global hidden state edge distribution, transition matrix and confusion matrix'''
        assert isinstance(train,list)
        assert isinstance(label,list)
        assert len(train) == len(label)
        self.train = train
        self.label = label
        self.cal_prob()
        self.cal_trans()
        self.cal_emit()
    def cal_prob(self):
        '''Generate global hidden state edge distribution'''
        prob = np.zeros(max(self.label)+1)
        for y in set(self.label):
            prob[y] += float(self.label.count(y)/len(self.label))
        self.prob = np.mat(prob)
    def cal_trans(self):
        '''Generate transfer matrix'''
        trans = np.zeros((len(set(self.label)),len(set(self.label))))
        last = self.label[0]
        for y in self.label[1:]:
            trans[last,y] += 1
            last = y
        self.trans = np.mat([row/row.sum() for row in trans])
    def cal_emit(self):
        '''Generation and emission(confusion)matrix'''
        emit = np.zeros((len(set(self.label)),len(set(self.train))))
        for x,y in zip(self.train,self.label):
            emit[y,x] += 1
        self.emit = np.mat([row/row.sum() for row in emit])
    def predict(self,test):
        '''Prediction of hidden state sequence based on explicit state'''
        assert isinstance(test,list)
        assert len(set(test)-set(np.arange(self.emit.shape[1]))) == 0
        seq = []
        for t in range(len(test)):
            if t == 0:
                pred = np.multiply(self.prob,self.emit[:,test[t]].T)    #Predict the hidden state at the initial time
            else:
                pred = np.multiply(pred*self.trans,self.emit[:,test[t]].T)    #Predict the hidden state at time T
            pred = pred/(pred.sum()+1e-12)    #Prevent overflow of calculation lower limit
            seq.append(pred.argmax())
        return seq
    def viterbi_predict(self,test):
        '''Viterbi Algorithm adjustment'''
        assert isinstance(test,list)
        assert len(set(test)-set(np.arange(self.emit.shape[1]))) == 0
        seq = []
        for t in range(len(test)):
            if t == 0:
                pred = np.multiply(self.prob,self.emit[:,test[t]].T)    #Predict the hidden state at the initial time
            else:
                pred = np.mat([(pred[0,y]*self.trans[:,y]).max() for y in range(pred.shape[1])])    #Add this line to the original model
                pred = np.multiply(pred,self.emit[:,test[t]].T)    #Predict the hidden state at time T
            pred = pred/(pred.sum()+1e-12)    #Prevent overflow of calculation lower limit
            t+=1
            seq.append(pred.argmax())
        return seq
if __name__ == '__main__':
    train = [0,5,2,6,4,3,2,0,5,1,5,1,2,5,2,0,2,0,2,3,6,4,6,4,2,5,1,0,2,5]
    label = [1,0,2,1,2,1,2,2,0,2,0,1,0,0,2,1,1,2,2,0,1,2,0,2,1,2,0,0,0,1]
    test = [0,2,3,6,3,1,1,2,2,5,1,5,4,2,3,6,2,5,0,5,2]
    model = HMM()
    model.fit(train,label)    #model training
    print('Prediction result (original): %s'%model.predict(test))    #model prediction
    print('Prediction result (Viterbi): %s'%model.viterbi_predict(test))    #Model prediction (Viterbi)

14.2 Markov random Airport

Markov Random Field (MRF) is a typical Markov network, which is a famous phase free graph model. Each node in the graph represents one or a group of variables, and the edge between nodes represents the dependency between the two variables. Markov random fields have a set of potential functions, also known as "factor s", which are non negative real functions defined on the subset of variables, mainly used to define probability distribution functions.
A simple Markov random field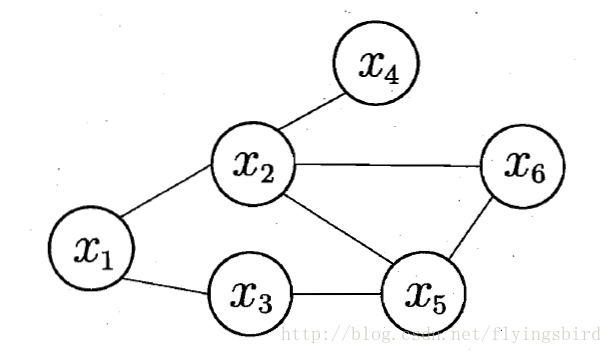

14.3 conditional random Airport
CRF (Conditional Random Fields) is the conditional probability distribution model of another group of output random variables given a set of input random variables. It is a discriminant probability undirected graph model. Since it is a discriminant, it is the conditional probability distribution model.

CRF is mostly used in the field of natural language processing and image processing. In NLP, it is a probabilistic model used to label and divide sequence data. According to the definition of CRF, relative sequence is a given observation sequence X and output sequence Y, and then the model is described by defining conditional probability P(Y|X).

The output random variable hypothesis of CRF is an undirected graph model or Markov random field, while the input random variable as a condition is not assumed to be Markov random field. Theoretically, the graph model structure of CRF can be given arbitrarily, but we usually define the special conditional random field on the online chain, which is called linear chain conditional random field.

14.4 learning and inference

14.5 approximate inference

14.6 topic model
1. LDA mathematical definition

1) Topic model: traditional text classifiers, such as Bayes, kNN and SVM, can only be divided into a certain category. Suppose I give three classifications of "algorithm", "segmentation" and "Literature" for judgment. If a classifier classifies the text into algorithm class, I think it's OK. If it classifies the segmentation, I think it's not accurate enough.

Suppose a young man of literature and art came to see my blog, he didn't know algorithm and participle at all, and he couldn't give specific alternative categories naturally. Is there a model that can tell this idiot that this article is probably (80%) talking about algorithm, or (19%) talking about participle, or (1%) talking about other topics?

Yes, such a model is a topic model.