Code to realize cross linked list and adjacency multiple list

0x01. Cross linked list

Origin:

Adjacency table is only suitable for judging the relevant information of a vertex's outgoing degree, while inverse adjacency table is only suitable for judging the relevant information of incoming degree. When it needs to judge at the same time, it needs to introduce a new structure: cross linked list.

Why is it called cross linked list?

First, let's look at the vertex structure of the cross linked list:

Data refers to the data field of the vertex; firstin refers to the first point of the vertex to the arc with the vertex as the arc head (vertex as the end point); firstout refers to the first point of the vertex to the arc with the vertex as the arc tail (vertex as the start point of the arc).

Then look at the edge table structure:

tailvex refers to the following table of the array of arc tail of the arc; headvex refers to the subscript of the array of arc head of the arc; headlink refers to the next edge with the same starting point; taillink refers to the next edge with the same ending point; info can also be called light, which records the weight of the edge.

Starting from a vertex, you can choose the first pointer to point to the edge, and then to a specific edge. You can also choose whether to point to the next edge with the same starting point or to the next edge with the same ending point. Each path has multiple choices, like a cross, so it is called a cross list.

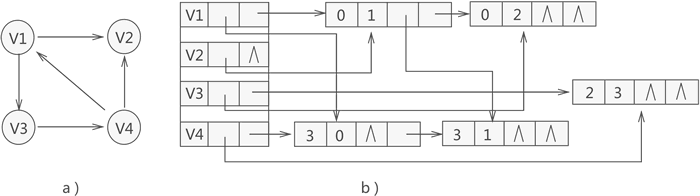
Note: the cross linked list is only applicable to directed graphs.

Cross linked list structure:

#define MAXSIZE 100

//Edge table structure
typedef struct EdgeNode
{
	int tailvex;//Subscript of arc starting point in vertex table
	int headvex;//Subscript of arc end point in vertex table
	struct EdgeNode* headlink;//Points to the next edge with the same starting point
	struct EdgeNode* taillink;//Points to the next edge with the same end point
	int weight;//Storage weight
}EdgeNode;

//Vertex table structure
typedef struct VexNode
{
	char data;//Vertex data field
	EdgeNode* firstin;//Edge header pointer with the vertex as the arc end point (arc head)
	EdgeNode* firstout;//Edge header pointer with the vertex as the arc start point (arc tail)
}VexNode,VexList[MAXSIZE];//At the same time, an array of vertex tables is created

//Structure of cross linked list
typedef struct
{
	VexList vexlist;//Vertex table
	int numv;//Vertex number
	int nume;//Edge number
}OLGraph;

Cross linked list creation:

void CreateOLGraph(OLGraph* G)
{
	int i, j, k, w;
	printf("Please enter the number of vertices and edges of the graph:\n");
	scanf("%d %d", &G->numv, &G->nume);
	while (getchar() != '\n');//Clear buffer
	for (i = 0; i < G->numv; i++)//Enter vertex information
	{
		scanf("%c", &G->vexlist[i].data);
		G->vexlist[i].firstin = NULL;//Initialization
		G->vexlist[i].firstout = NULL;
	}
	for (k = 0; k < G->nume; k++)//Input side information
	{
		printf("Please enter the subscript of the starting point of the arc in the array, the subscript of the ending point in the array, and the weight:\n");
		while (getchar() != '\n');//Clear buffer
		scanf("%d %d %d", &i, &j, &w);
		EdgeNode* e = (EdgeNode*)malloc(sizeof(EdgeNode));
		e->tailvex = i;
		e->headvex = j;
		e->weight=w;
		e->headlink = G->vexlist[j].firstin;//Head insertion
		e->taillink = G->vexlist[i].firstout;//Head insertion
		G->vexlist[j].firstin = e;
		G->vexlist[i].firstout = e;
	}
}

General traversal of cross linked list:

void PrintOLGraph(OLGraph G)
{
	for (int i = 0; i < G.numv; i++)
	{
		EdgeNode* p = G.vexlist[i].firstin;
		printf("Vertex %c The edge of the head has:\n", G.vexlist[i].data);
		int numhead = 0;//Record in degrees
		while (p)
		{
			printf("vertex %c To the vertex %c ，Weight is %d \n",G.vexlist[p->tailvex].data,G.vexlist[p->headvex].data,p->weight);
			numhead++;
			p = p->headlink;
		}
		printf("The entry of this vertex is %d \n", numhead);
		printf("Vertex %c The tail edges are:\n", G.vexlist[i].data);
		int numtail = 0;//Record the degree
		p = G.vexlist[i].firstout;
		while (p)
		{
			printf("vertex %c To the vertex %c ，Weight is %d \n", G.vexlist[p->tailvex].data, G.vexlist[p->headvex].data, p->weight);
			numtail++;
			p = p->taillink;
		}
		printf("The vertex's degree is %d \n", numtail);
	}
}

0x02. Adjacency multiple table

Origin:

For the adjacency list of undirected graph, if we pay more attention to the operation of marking the visited edge and deleting the edge, we need to use adjacency multiple tables.

Structure diagram of vertex table:

The vertex structure is the same as the adjacency table, data refers to the data domain, and firstedge refers to the first pointed edge.

Side table structure:

• mark: used as a flag variable to record whether the node on this side has been accessed;
• ivex: record the subscript of the edge end in the vertex array;
• jvex: subscript in vertex array at the other end of edge recording;
• ilink: pointer to the next edge associated with i end;
• jlink: pointer to the next side associated with the j end;

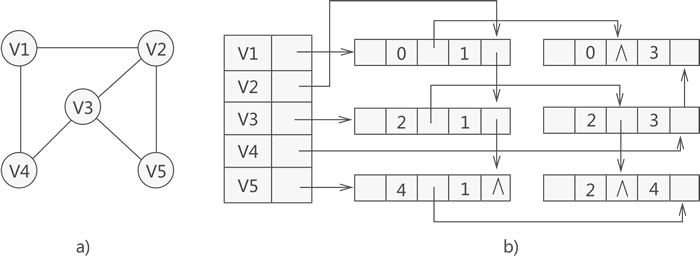
Structure:

#define MAXSIZE 100

//Edge table structure
typedef struct EdgeNode
{
	int mark;//Flag domain 0 is not accessed 1 is accessed
	int ivex;//Edge i ends
	int jvex;//j end of edge
	struct EdgeNode* ilink;//Point to the edge related to i
	struct EdgeNode* jlink;//Point to the edge associated with j
	int weight;
}EdgeNode;

//Vertex table structure
typedef struct VexNode
{
	char data;
	struct EdgeNode* firstedge;
}VexNode,AdjList[MAXSIZE];

//Adjacency multiple table structure
typedef struct
{
	AdjList adjlist;
	int numv;
	int nume;
}AMLGraph;

Adjacency multiple table creation:

void CreateAMLGraph(AMLGraph* G)
{
	int i, j, k, w;
	printf("Please enter the number of vertices and edges of the graph:\n");
	scanf("%d %d", &G->numv, &G->nume);
	while (getchar() != '\n');//Clear buffer
	for (i = 0; i < G->numv; i++)
	{
		scanf("%c", &G->adjlist[i].data);
		G->adjlist[i].firstedge  = NULL;//Initialization
	}
	for (k = 0; k < G->nume; k++)
	{
		printf("Please enter the subscript of the two vertices of the edge in the array and the weight of the edge:\n");
		while (getchar() != '\n');//Clear buffer
		scanf("%d %d %d", &i, &j, &w);
		EdgeNode* e = (EdgeNode*)malloc(sizeof(EdgeNode));
		e->mark = 0;
		e->ivex = i;
		e->jvex = j;
		e->weight = w;
		e->ilink = G->adjlist[i].firstedge;
		e->jlink = G->adjlist[j].firstedge;
		G->adjlist[i].firstedge = e;
		G->adjlist[j].firstedge = e;
	}
}

Common traversal adjacency multiple tables:

void PrintAMLGraph(AMLGraph G)
{
	for (int i = 0; i < G.numv; i++)
	{
		EdgeNode* p = G.adjlist[i].firstedge;
		printf("And vertex %c The relevant sides are:", G.adjlist[i].data);
		while (p)
		{
			if (p->ivex == i)//Determine which end of time edge is equal to i
			{
				//If (P - > mark = = 1) / / when an edge needs to be accessed once, the flag variable is used. Otherwise, it is not used
				//{
					printf("%c reach %c ，Weight is %d\t", G.adjlist[p->ivex].data, G.adjlist[p->jvex].data, p->weight);
					//p->mark = 1;
				//}
				p = p->ilink;
			}
			else
			{
				//if (p->mark == 0)
				//{
					printf("%c reach %c ，Weight is %d\t", G.adjlist[p->jvex].data, G.adjlist[p->ivex].data, p->weight);
					//p->mark = 1;
				//}
				p = p->jlink;
			}
			printf("\n");
		}
	}
}

0x03. Edge set array

Meaning: it is also a storage structure of a graph, which is composed of two one-dimensional arrays, a one-dimensional array stores the information of vertices and a one-dimensional array stores the information of edges. Each element of the edge array is composed of the start subscript, the end subscript and the weight.

Note: this storage structure pays great attention to the set of edges. If you need to operate on vertices, you need to traverse the entire edge array, which is inefficient and not commonly used.

The end of this chapter.