A Euclid (Law)

Thought: Fibonacci series can be formed after the third term of hand pushing law is found.

#include<bits/stdc++.h>
using namespace std;
 
typedef long long ll;
const int maxn=82;
ll fib[maxn]={1,3,5};
 
int main(){
    for(int i=3;i<=maxn;i++) fib[i]=fib[i-1]+fib[i-2];
    int T; scanf("%d",&T);
    while(T--){
        int n; scanf("%d",&n);
        printf("%lld\n",fib[n]);
    }
    return 0;
}

B bracket sequence (greedy)

   idea: Classic greedy problem. When we encounter the left half, we store the characters in the stack. When we encounter the right half, we check whether the top of the stack is the left half (when the top of the stack is empty at this time). If it matches, the top of the stack pops up. If it doesn't match, we can put it in the top of the stack. Finally, check whether there are any characters in the stack (if all the characters match, then all the characters in the stack will pop up).

#include<bits/stdc++.h>
using namespace std;
 
typedef long long ll;
const int maxn=1e6+10;
char str[maxn];
 
stack<char>s;
 
int main(){
    scanf("%s",str);
    int n=strlen(str);
    for(int i=0;i<n;i++){
        if(str[i]=='('||str[i]=='{'||str[i]=='['||!s.size()){
            s.push(str[i]); continue;
        }
        if(str[i]==')'){
            if(s.top()=='(') s.pop();
            else s.push(str[i]);
        }else if(str[i]==']'){
            if(s.top()=='[') s.pop();
            else s.push(str[i]);
        }else if(str[i]=='}'){
            if(s.top()=='{') s.pop();
            else s.push(str[i]);
        }
    }
    if(s.size()) puts("No");
    else puts("Yes");
    return 0;
}

C-subsegment product (fractional modular)

                               . At this time, when none of the conditions in the interval is 000, we first calculate the product ans ans ans of the number of K K K. When we are going to the right, what we need to do is (ANS * a[i]/a[i − k])%mod(ans*a[i]/a[i-k])\%mod(ans * a[i]/a[i − k])%mod. If I don't deal with the situation of 000 as I said above, then we have the situation of * 0 and / 0 * 0 and / 0 * 0 and / 0 in the process of simulating the above.

#include<bits/stdc++.h>
using namespace std;
 
typedef long long ll;
const int mod=998244353;
const int maxn=2e5+10;
int a[maxn];
 
ll quickPow(ll a,ll b){
    ll ans=1,res=a;
    while(b){
        if(b&1) ans=ans*res%mod;
        res=res*res%mod;
        b>>=1;
    }
    return ans%mod;
}
 
int main(){
    int n,k; scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    if(k>=n){
        ll sum=1;
        for(int i=1;i<=n;i++) sum=sum*a[i]%mod;
        printf("%lld\n",sum);
    }else{
        ll sum=1,cnt=0,mmax=0;
        for(int i=1;i<=n;i++){
            cnt++;
            if(a[i]==0) { cnt=0;sum=1;continue; }
            sum=sum*a[i]%mod;
            if(cnt==k) mmax=max(mmax,sum);
            if(cnt==k+1){
                cnt--;
                sum=sum*quickPow(a[i-k],mod-2)%mod;
                mmax=max(mmax,sum);
            }
        }
        printf("%lld\n",mmax);
    }
    return 0;
}

D-segment exclusive or (exclusive or property)

Idea: we know that AAA ^ AAA = 000000 ^ A=AA=AA=A, we first maintain a prefix exclusive or and, as shown in the figure:

] = sum [9] sum [5] = sum [6] = sum [7] = sum [8] = sum [9], if there is I < Ji < Ji < J, there are:
  sum[i]=a[1sum[i] = a[1sum[i]=a[1] ^ a[2a[2a[2] ^ ............ ^ a[i]a[i]a[i]      sum[i]=sum[j]sum[i] = sum[j]sum[i]=sum[j]
  sum[j]=a[1]sum[j] = a[1]sum[j]=a[1] ^ a[2]a[2]a[2] *^ ............ ^ a[i]a[i]a[i] ^ a[i+1]a[i+1]a[i+1] ^ ............ ^ a[j]=sum[j]a[j] = sum[j]a[j]=sum[j] ^ a[i+1]a[i+1]a[i+1] ^ ............ ^ a[j]a[j]a[j]
Then a [i + 1] a [i + 1] a [i + 1] ^........ ^ a [J] = 0A [J] = 0A [J] = 0
                    , so we only need to know the number of times sumsum appears. If it is 000, then we need to count our own 000. We can find two intervals: CNT * (CNT + 1)/2cnt*(cnt-1)/2cnt * (cnt-1) / 2. If a number has been calculated, then there is no need to calculate the interval satisfying the question.

//My program is complex. I can directly open cnt [] array and calculate how many times each number appears.
#include<bits/stdc++.h>
using namespace std;
 
typedef long long ll;
const int maxn=2e5+10;
ll a[maxn],sum[maxn],sum1[maxn];
map<ll,int>m;
 
int main(){
    //cout<<(2^3^4^5)<<endl;
    int n; scanf("%d",&n);
    for(int i=0;i<n;i++){
        scanf("%lld",&a[i]);
        if(i) sum[i]=sum[i-1]^a[i];
        else sum[i]=a[i];
        sum1[i]=sum[i];
        m[sum[i]]=1;
    }
    //for(int i=0;i<n;i++) cout<<sum[i]<<" "; cout<<endl;
    sort(sum1,sum1+n);
    ll ans=0;
    for(int i=0;i<n;i++){
        int l=lower_bound(sum1,sum1+n,sum[i])-sum1;
        int r=upper_bound(sum1,sum1+n,sum[i])-sum1-1;
        ll cnt=r-l+1;
        if(m[sum[i]]){
            if(sum[i]==0){
                ans+=cnt*(cnt+1)/2;
            }else{
                ans+=cnt*(cnt-1)/2;
            }
            m[sum[i]]=0;
        }
    }
    printf("%lld\n",ans);
    return 0;
}

                             the above idea is actually complicated. We can record the number of times of sumsum and calculate the range that meets the conditions. In the process of calculating the m[0]=1m[0]=1m[0]=1.

#include<bits/stdc++.h>
using namespace std;
 
typedef long long ll;
const int maxn=2e5+10;
ll a[maxn],sum[maxn];
map<ll,int>m;
 
int main(){
    int n; scanf("%d",&n);
    ll ans=0; m[0]=1;
    for(int i=1;i<=n;i++){
        scanf("%lld",&a[i]);
        sum[i]=sum[i-1]^a[i];
        //cout<<sum[i]<<" "<<m[sum[i]]<<endl;
        ans+=(ll)m[sum[i]];
        m[sum[i]]++;
    }
    printf("%lld\n",ans);
    return 0;
}

E minimum expression (thinking + large number)

                              : first, we put all the numerical characters into another Group, I put these numeric characters into a two-dimensional array in the competition, and then add large numbers. This method is timeout, but I can't think of other methods. After the game, we saw the solution to the problem and knew that we can add directly by bits, that is, we can traverse from the back to the front, each time passing s.size()+1s.size()+1s.size()+1 number, it means carry once. (because we want to divide these numbers into s.size()+1s.size()+1s.size()+1 group, then from the back to the front, the first s.size() + 1s. Size() + 1 number must be one digit of each group. We can add them up. The next s.size()+1s.size()+1s.size()+1 number is ten digits, and so on until all are calculated. In this way, the final result can be obtained by calculating each bit while carrying.

#include<bits/stdc++.h>
using namespace std;
 
typedef long long ll;
const int maxn=5e5+10;
char str[maxn],str1[maxn];
int ans[maxn];
 
stack<int>s;
 
int main(){
    scanf("%s",str);
    int n=strlen(str);
    int cnt=0;
    for(int i=0;i<n;i++){
        if(str[i]=='+') s.push(str[i]);
        else str1[cnt++]=str[i];
    }
    sort(str1,str1+cnt);
    //puts(str1);
    int len=0,cntNumber=0;
    for(int i=cnt-1;i>=0;i--){
        cntNumber++;
        if(cntNumber==(int)s.size()+1||i==0){
            ans[len++]+=str1[i]-'0';
            ans[len]=ans[len-1]/10;
            ans[len-1]%=10;
            cntNumber=0;
        }else ans[len]+=str1[i]-'0';
    }
    if(ans[len]) printf("%d",ans[len]);
    for(int i=len-1;i>=0;i--) printf("%d",ans[i]);
    return 0;
}

F-tree game (thinking + search)

Idea: the winning strategy: the distance between two people is even. The distance between each point and root node can be calculated directly by using dfsdfsdfs or bfsbfsbfs. The distance is calculated as follows: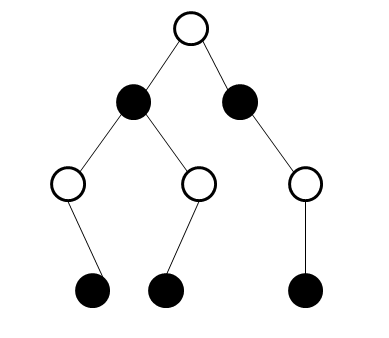

                        .

//dfs
#include<bits/stdc++.h>
using namespace std;
 
typedef long long ll;
const int maxn=1e6+10;
int cnt=0,head[maxn],deep[maxn]={-1};
 
struct Edge{
    int u,v,next;
}edge[maxn<<1];
 
void addedge(int u,int v){
    edge[cnt].u=u;
    edge[cnt].v=v;
    edge[cnt].next=head[u];
    head[u]=cnt++;
}
 
void dfs(int fa,int v){
    deep[v]=deep[fa]+1;
    for(int i=head[v];i!=-1;i=edge[i].next){
        if(edge[i].v==fa) continue;
        dfs(v,edge[i].v);
    }
}
 
int main(){
    int n; scanf("%d",&n);
    for(int i=1;i<=n;i++) head[i]=-1;
    for(int i=2;i<=n;i++){
        int fa; scanf("%d",&fa);
        addedge(fa,i); addedge(i,fa);
    }
    dfs(0,1);
    int cnt0=0,cnt1=0;
    for(int i=1;i<=n;i++){
        if(deep[i]&1) cnt1++;
        else cnt0++;
    }
    ll ans=1ll*(cnt0-1)*cnt0;
    ans+=1ll*cnt1*(cnt1-1);
    printf("%lld\n",ans);
    return 0;
}

#include<bits/stdc++.h>
using namespace std;
 
typedef long long ll;
const int maxn=1e6+10;
int cnt=0,head[maxn],deep[maxn];
bool vis[maxn];
 
struct Edge{
    int u,v,next;
}edge[maxn<<1];
 
struct Node{
    int n,deep;
    Node(){};
    Node(int n,int deep):n(n),deep(deep){};
};
 
void addedge(int u,int v){
    edge[cnt].u=u;
    edge[cnt].v=v;
    edge[cnt].next=head[u];
    head[u]=cnt++;
}
 
void bfs(int s){
    queue<Node>q; q.push(Node(s,0));
    while(!q.empty()){
        Node node=q.front(); q.pop();
        deep[node.n]=node.deep;
        for(int i=head[node.n];i!=-1;i=edge[i].next){
            if(!vis[edge[i].v]){
                vis[edge[i].v]=true;
                q.push(Node(edge[i].v,node.deep+1));
            }
        }
    }
}
 
int main(){
    int n; scanf("%d",&n);
    for(int i=1;i<=n;i++) head[i]=-1;
    for(int i=2;i<=n;i++){
        int fa; scanf("%d",&fa);
        addedge(fa,i); addedge(i,fa);
    }
    bfs(1);
    int cnt0=0,cnt1=0;
    for(int i=1;i<=n;i++){
        if(deep[i]&1) cnt1++;
        else cnt0++;
    }
    ll ans=1ll*cnt0*(cnt0-1);
    ans+=1ll*cnt1*(cnt1-1);
    printf("%lld\n",ans);
    return 0;
}

I match stars (greed + STL)

Let's first look at a three-dimensional coordinate map

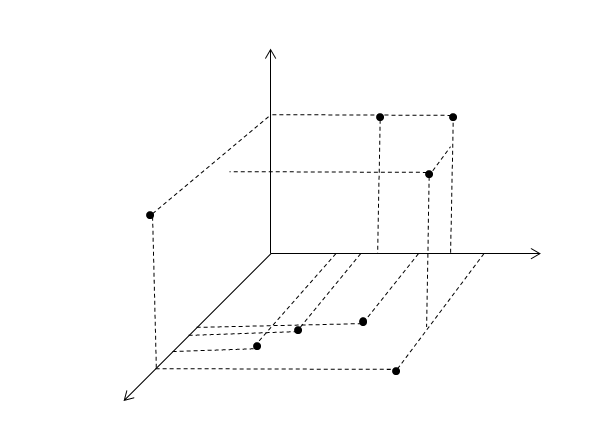
   we sort these points according to x x x first. If xxx is the same, we sort them according to z Z z, and then we traverse the array. If we traverse to a point whose zzz is 000, then we store its yyy value in multisetmultiset multiset. If zzz of this point is 111, then we store x, zx, zx, z of yyy point before The value must be smaller than the current value. We only need to pay attention to yyy. As long as we can find a point smaller than the current point's yyy value, we can complete pairing and delete the point from multisetmultisetmultiset. We use multisetmultisetmultiset dichotomy to find the position of the iterator ≥ y ≥ y, so the value stored in the previous position must be smaller than yyy (if the current position of the iterator is not s.begin()s.begin()s.begin()), and delete the value on the previous position of the iterator after finding it, and add one to the matching value.

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
 
struct Node{
    int x,y,z;
    bool operator<(const Node &node) const{
        if(x==node.x) return z<node.z;
        return x<node.x;
    }
}node[maxn];
 
multiset<int>ms;
 
int main(){
    int n; scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d%d%d",&node[i].x,&node[i].y,&node[i].z);
    sort(node+1,node+n+1);
    int ans=0;
    for(int i=1;i<=n;i++){
        if(node[i].z==0) ms.insert(node[i].y);
        else{
            //>=The position of the first iterator of the current point y, the previous position is the point to be found to match
            multiset<int>::iterator it=ms.lower_bound(node[i].y);
            if(it==ms.begin()) continue;
            ms.erase(--it);
            ans++;
        }
    }
    printf("%d\n",ans);
    return 0;
}