Traditional machine learning has a lot of algorithms. The KNN that I sorted out in my last article is a kind of algorithm. The decision tree that I will talk about in this article is also a very important algorithm. Of course, it should be explained in advance that these algorithms also have a lot of small knowledge points and classifications. I'm only going to follow my own technology with the most classic algorithm (or entry algorithm, and my own understanding of it) In the later stage of the upgrade, we will add them one by one.

I think there are more comprehensive theoretical knowledge about decision tree than I sorted out, so I'll share it here: Decision tree (classification tree, regression tree) But I only share my own feelings, so readers must carefully look at the relevant articles mentioned in the process of reading the article and code of this article, standing on the shoulders of giants to see further, of course, this article will not mention all the concepts related to decision tree, welcome to add suggestions.

Before recording my learning path, I would like to mention that you are very welcome to join our communication group. You can discuss all the relevant contents. I will also share all the resources including my article resources to you, learn together and make progress. Welcome to join the group~~~

1, Related concepts and understanding of decision tree

Note: the concepts contained in the related concepts are only necessary and important in my opinion, but they are not complete.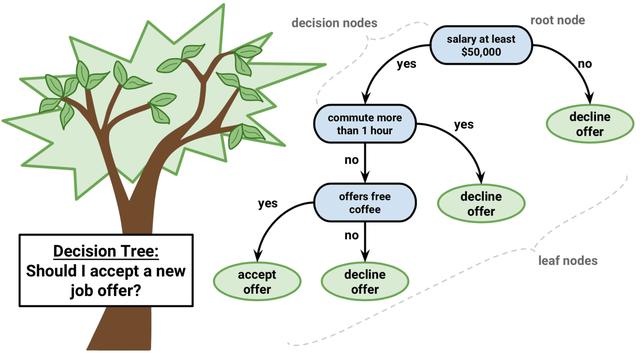

Personal understanding:

The decision tree can be understood as a process of building (inverted tree), and the algorithm we build is the tool to complete this "tree". You may wonder what is the role of machine learning here?

Yes, machine learning is used to extract relevant information (Shannon entropy and information gain) from a number of training sets, that is to say, the tree we built contains potential information or internal information for relevant events or data, and pre judgment (essentially classification) is carried out with these information.

Of course, you can also say that people can also extract these information, which is nothing more than the decision-making problem in different situations. Of course, but if the influencing factors (feature dimensions) of a thing are far greater than the processing limit of people, it needs the help of decision tree algorithm (or other algorithms).

The essence of decision tree algorithm is the problem of ranking different features (calculating the corresponding information gain)

Here's a chestnut:

When a girl goes to a blind date, the condition of blind date is whether to rank first in terms of having a house and a car or to rank first in terms of ambition. This is the problem of decision tree.

• Information entropy
• Information gain

Information entropy: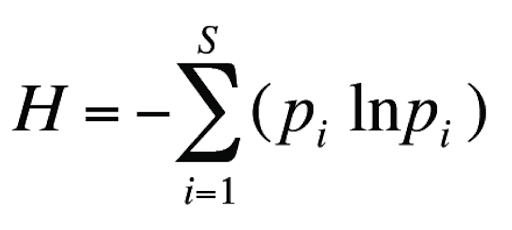

Among them, P is the probability of the corresponding event (this concept seems simple, but it can be further understood only through careful experience in the actual operation and use process). ln can also be replaced by the corresponding log2

Information gain:

g(D,A)=H(D)-H(D|A)

The information gain g(D,A) of feature A to training data set D is the difference between the entropy H(D) of set D and the conditional entropy H(D|A) of D under the given condition of feature A.

In other words, the information gain is relative to the feature. The larger the information gain is, the greater the impact of the feature on the final classification result will be. We should select the feature that has the greatest impact on the final classification result as our classification feature.

2, Decision tree generation of loan decision tree in practice

First is the loan data description:
Age: 0 Youth 1 middle age 2 old

Work or not: 0 No 1 yes

Have your own house: 0 No 1 yes

Credit situation: 0 No 1 yes

Whether to lend: this group of data determines whether to lend at last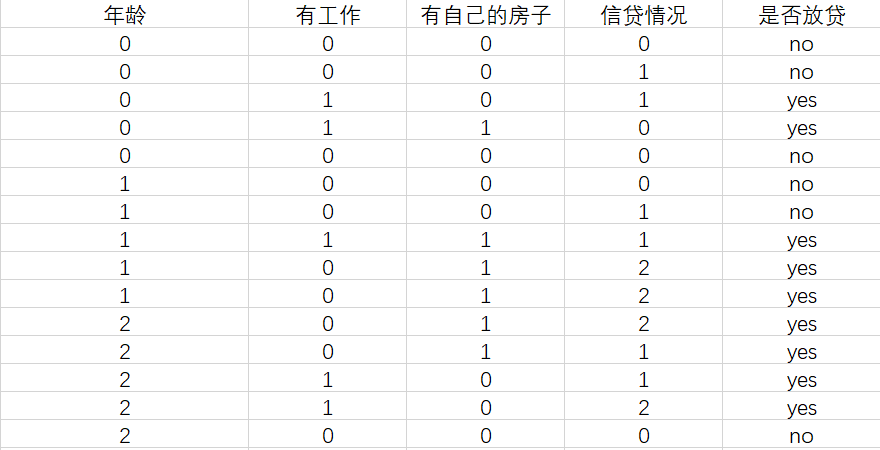

Objective: to build a decision tree of lending judgment based on the above data, so as to facilitate lending judgment in the future.

show me the code

Description: mainly from the big guy jack-cui There are some changes, and the infringement is deleted

**Code learning method: * * I think the most effective way to learn and absorb is to read other people's code, and to actively read other people's code by breaking points.

Big guy's code is concise and perfect, but the best way to read it is to use pycharm's breakpoint function to mark breakpoints where you have questions or want to understand deeply and read them line by line. Only after repeated reading and learning can you have your own opinions on the code from the theoretical level.

The last and the most important step of sublimation is from simplicity to complexity. Find a decision tree example and start from scratch. Think about it and write it again. Even if the code is not standardized, it should be completed independently. In the middle, solve your own problems by searching. This process is the precipitation process of learning.

from math import log
import operator
import matplotlib as plt
from matplotlib.font_manager import FontProperties

"""
//Function Description: calculate the empirical entropy (Shannon entropy) of a given data set

Parameters:
    dataSet - data set
Returns:
    shannonEnt - Empirical entropy(Shannon entropy)
Author:
    Jack Cui
Modify:
    2017-03-29
"""
def calcShannonEnt(dataSet):
    numEntires = len(dataSet)                        #Returns the number of rows in the dataset
    labelCounts = {}                                #Save a dictionary of the number of occurrences of each label
    for featVec in dataSet:                            #Statistics of each group of eigenvectors
        currentLabel = featVec[-1]                    #Extract label information
        if currentLabel not in labelCounts.keys():    #If the label is not put into the dictionary of statistics times, add it
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1                #Label count
    shannonEnt = 0.0                                #Empirical entropy (Shannon entropy)
    for key in labelCounts:                            #Calculating Shannon entropy
        prob = float(labelCounts[key]) / numEntires    #Probability of selecting the label
        shannonEnt -= prob * log(prob, 2)            #Calculation by formula
    return shannonEnt                                #Return to empirical entropy (Shannon entropy)

"""
//Function Description: create test data set

Parameters:
    //nothing
Returns:
    dataSet - data set
    //Data Description:
     //Age (0 / 1 / 2), work (0 / 1), own house (0 / 1), credit situation (0 / 1 / 2), category (whether or not individual loan) (yes / no)
    labels - Categorical attribute
Author:
    Jack Cui
Modify:
    2017-07-20
"""
def createDataSet():
    dataSet = [[0, 0, 0, 0, 'no'],                        #data set
            [0, 0, 0, 1, 'no'],
            [0, 1, 0, 1, 'yes'],
            [0, 1, 1, 0, 'yes'],
            [0, 0, 0, 0, 'no'],
            [1, 0, 0, 0, 'no'],
            [1, 0, 0, 1, 'no'],
            [1, 1, 1, 1, 'yes'],
            [1, 0, 1, 2, 'yes'],
            [1, 0, 1, 2, 'yes'],
            [2, 0, 1, 2, 'yes'],
            [2, 0, 1, 1, 'yes'],
            [2, 1, 0, 1, 'yes'],
            [2, 1, 0, 2, 'yes'],
            [2, 0, 0, 0, 'no']]
    labels = ['Age', 'Have a job', 'Have your own house', 'Credit situation']		#Categorical attribute
    return dataSet, labels                             #Return dataset and classification properties

"""
//Function Description: divide data set according to given characteristics

Parameters:
    dataSet - Data set to be divided
    axis - Characteristics of partitioned datasets,That is, to judge the relevant information of corresponding features (Shannon entropy and information gain)
    value - The value of the feature to be returned. Judge whether the corresponding feature is equal to the corresponding value
Returns:
    //nothing
Author:
    Jack Cui
Modify:
    2017-03-30
"""
def splitDataSet(dataSet, axis, value):
    retDataSet = []                                        #Create a list of returned datasets
    for featVec in dataSet:                             #Traversal data set
        print(featVec)
        if featVec[axis] == value:

            reducedFeatVec = featVec[:axis]                #Remove axis features
            print(featVec[axis+1:])
            reducedFeatVec.extend(featVec[axis+1:])     #Add eligible to returned dataset
            retDataSet.append(reducedFeatVec)
            print(retDataSet)
    return retDataSet                                      #Return the partitioned dataset

"""
//Function Description: select the best feature

Parameters:
    dataSet - data set
Returns:
    bestFeature - Maximum information gain(optimal)Index value of characteristic
Author:
    Jack Cui
Modify:
    2017-03-30
"""
def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1                    #Characteristic quantity
    baseEntropy = calcShannonEnt(dataSet)                 #Shannon entropy of computing data set
    bestInfoGain = 0.0                                  #information gain
    bestFeature = -1                                    #Index value of optimal feature
    for i in range(numFeatures):                         #Traverse all features, that is, all columns
        #Get all the i-th features of the dataSet
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)                         #Create set set {}, element is not repeatable
        newEntropy = 0.0                                  #Empirical conditional entropy
        for value in uniqueVals:                         #Calculate information gain
            subDataSet = splitDataSet(dataSet, i, value)         #Subset after the Division
            prob = len(subDataSet) / float(len(dataSet))           #Calculating the probability of subsets
            newEntropy += prob * calcShannonEnt(subDataSet)     #According to the formula, the empirical conditional entropy is calculated, and the information gain is equal to Shannon entropy minus conditional entropy
        infoGain = baseEntropy - newEntropy                     #The problem of information gain is actually to judge the decision tree by judging the feature priority

        print("The first%d The gain of the features is%.3f" % (i, infoGain))            #Print the information gain of each feature
        if (infoGain > bestInfoGain):                             #Calculate information gain
            bestInfoGain = infoGain                             #Update the information gain to find the maximum information gain
            bestFeature = i                                     #The index value of the feature with the largest gain of recorded information
    return bestFeature                                           #Returns the index value of the feature with the largest information gain

"""
//Function Description: count the most elements (class labels) in the classList

Parameters:
    classList - Class label list
Returns:
    sortedClassCount[0][0] - Most elements here(Class labels)
Author:
    Jack Cui
Blog:
    http://blog.csdn.net/c406495762
Modify:
    2017-07-24
"""
def majorityCnt(classList):
    classCount = {}
    for vote in classList:                                        #Count the number of occurrences of each element in the classList
        if vote not in classCount.keys():classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.items(), key = operator.itemgetter(1), reverse = True)        #Sort by dictionary value in descending order
    return sortedClassCount[0][0]

"""
//Function Description: create decision tree

Parameters:
    dataSet - Training data set
    labels - Classification property label
    featLabels - Optimal feature label for storage selection
Returns:
    myTree - Decision tree
Author:
    Jack Cui
Blog:
    http://blog.csdn.net/c406495762
Modify:
    2017-07-25
"""
def createTree(dataSet, labels, featLabels):
    classList = [example[-1] for example in dataSet]            #Take the classification label (yes or no)
    if classList.count(classList[0]) == len(classList):            #Stop dividing if the categories are identical
        return classList[0]
    if len(dataSet[0]) == 1:                                    #Return the most frequent class label when traversing all features
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)                #Select the best feature
    bestFeatLabel = labels[bestFeat]                            #Label of optimal feature
    featLabels.append(bestFeatLabel)
    myTree = {bestFeatLabel:{}}                                    #Tag generation tree based on optimal features
    del(labels[bestFeat])                                        #Delete used feature labels
    featValues = [example[bestFeat] for example in dataSet]        #Get the attribute values of all the best features in the training set
    uniqueVals = set(featValues)                                #Remove duplicate property values
    for value in uniqueVals:                                    #Traverse the feature and create a decision tree.
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), labels, featLabels)
    return myTree



if __name__ == '__main__':
    dataSet, labels = createDataSet()
    featLabels = []
    myTree = createTree(dataSet, labels, featLabels)
    print(myTree)