Refer to Chapter 7 of algorithm diagram for details. The original book was written in python, and I wrote it again in PHP, which was slightly improved

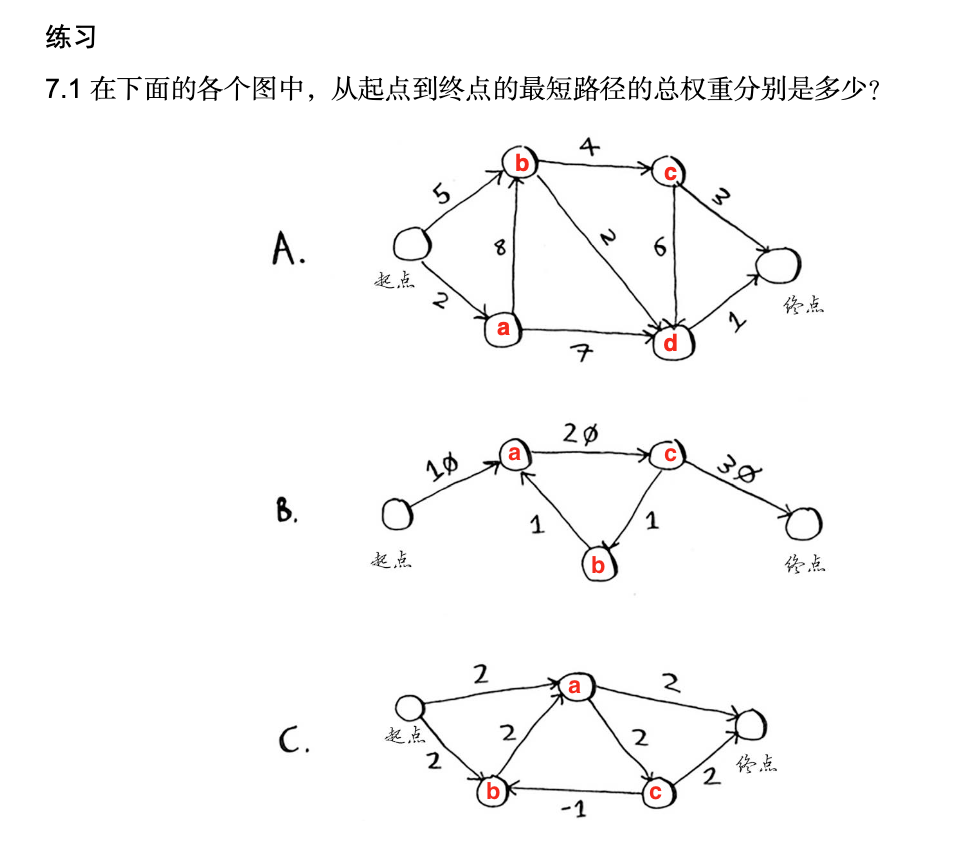
Test these three exercises in the book

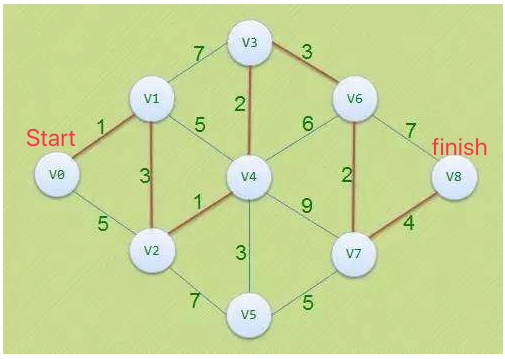
I found another "difficult" question on the Internet

Upper Code:

class ShortPath{
    protected $graph=[];//A graph can be represented only by storing the neighbors corresponding to each node

    protected $parents=[];//Save the parent relationship, and finally backtrack the shortest path through this array

    protected $costs;//Cost from start to each node

    protected $infinity=999999;//Use a large number to represent a positive infinity

    protected $processed=[];//key of processed node


    public function __construct($graph)
    {
        $this->graph=$graph;

        //Initialize the parent array, that is, only the neighbors of start are known, that is, the parent of start
        foreach ($this->graph['start'] as $k=>$v) {
            $this->parents[$k]='start';
        }

        //Initialize the cost array, that is, only the cost of the neighbor node of start is known, and all other nodes are positive infinite
        foreach ($this->graph as $k=>$v) {
            if($k=='start'){
                $this->costs=$this->graph['start'];
            }elseif(empty($this->costs[$k])){
                $this->costs[$k]=$this->infinity;
            }
        }
        $this->costs['finish']=$this->infinity;
    }

    public function find(){
        $nodeKey=$this->findLowestCostNode($this->costs);
        while ($nodeKey){//As long as there are unprocessed nodes
            $cost=$this->costs[$nodeKey];
            $neighbors=$this->graph[$nodeKey] ?? [];//Take neighbors
            //Traversing neighbors
            foreach ($neighbors as $k=> $v) {
                $newCost=$cost+$v;
                if($this->costs[$k] > $newCost){
                    $this->costs[$k]=$newCost;//Update lower overhead
                    $this->parents[$k]=$nodeKey;
                }
            }

            //Debug output
            echo 'Current node:' .$nodeKey . PHP_EOL;
            echo 'Neighbours:' . PHP_EOL;
            print_r($neighbors);
            echo 'Expenses:' . PHP_EOL;
            print_r($this->costs);

            //Now that all neighbors of the node have been processed, mark the node as processed
            $this->processed[]=$nodeKey;
            //Find the next node to be processed
            $nodeKey=$this->findLowestCostNode();
        }
        $this->showResult();
    }

    //Find the shortest one among the unprocessed nodes
    protected function findLowestCostNode(){
        $lowestCost=$this->infinity;//Set positive infinity here so that when you first enter the loop, it must be larger than the first element
        $lowestCostKey=false;//The key of the shortest path node to return
        foreach ($this->costs as $k=>$v) {
            if($v<$lowestCost && !in_array($k,$this->processed)){
                $lowestCost=$v;
                $lowestCostKey=$k;
            }
        }
        return $lowestCostKey;
    }

    //Beautify display processing results
    protected function showResult(){
        $path=[];
        $key='finish';
        //From the end, find the parent and trace back the shortest route
        while (isset($this->parents[$key])){
            array_unshift($path,$key);
            $key=$this->parents[$key];
        }
        echo 'The shortest path length is:' . $this->costs['finish'] . PHP_EOL;
        echo 'The route is:start->' . implode('->',$path) . PHP_EOL;
    }

}

//Corresponding exercise A
$graph1=[
    "start"=>[
        "a"=>2,
        "b"=>5,
    ],
    "a"=>[
        "b"=>8,
        "d"=>7,
    ],
    "b"=>[
        "c"=>4,
        "d"=>2,
    ],
    "c"=>[
        "finish"=>3,
        "d"=>6
    ],
    "d"=>[
        "finish"=>1
    ]
];

//Corresponding Exercise B
$graph2=[
    "start"=>[
        "a"=>10,
    ],
    "a"=>[
        "c"=>20,
    ],
    "b"=>[
        "a"=>1,
    ],
    "c"=>[
        "b"=>1,
        "finish"=>30,
    ],
];


//Corresponding exercise C. It can be seen that the algorithm is not suitable for the case with negative weight edges
$graph3=[
    "start"=>[
        "a"=>2,
        "b"=>2,
    ],
    "a"=>[
        "c"=>2,
        "finish"=>2
    ],
    "b"=>[
        "a"=>2,
    ],
    "c"=>[
        "b"=>-100,
        "finish"=>2,
    ],
];

//Corresponding to the last question, change v0 in the figure to start and v8 to finish
$graph4=[
    "start"=>[
        "v1"=>1,
        "v2"=>5,
    ],
    "v1"=>[
        "start"=>1,
        "v2"=>3,
        "v3"=>7,
        "v4"=>5,
    ],
    "v2"=>[
        "start"=>5,
        "v1"=>3,
        "v4"=>1,
    ],
    "v3"=>[
        "v1"=>7,
        "v2"=>2,
        "v6"=>3,
    ],
    "v4"=>[
        "v1"=>5,
        "v2"=>1,
        "v3"=>2,
        "v5"=>3,
        "v6"=>6,
        "v7"=>9,
    ],
    "v5"=>[
        "v2"=>6,
        "v4"=>3,
        "v7"=>5,
    ],
    "v6"=>[
        "v3"=>3,
        "v4"=>6,
        "v7"=>2,
        "finish"=>7
    ],
    "v7"=>[
        "v4"=>9,
        "v5"=>5,
        "v6"=>2,
        "finish"=>4
    ],
];

$obj=new ShortPath($graph4);
$obj->find();

Output of the last question

Finally, the pdf version of the book "algorithm diagram" is attached

Link: https://pan.baidu.com/s/1nditk7wayn7c9fz3ldngw password: ij0r