1. Understand hash function and hash table

Hash function and its importance are often tested in the topic of big data. Here are some concepts related to hash functions:

1.1 what is Hash

Hash (hash), also known as "hash".

hash originally means "hybrid", "patchwork" and "rephrase".

To some extent, hashing is the opposite operation of sorting. Sorting is to arrange the elements in a collection in a certain way, such as dictionary order. By calculating hash value, hashing breaks the original relationship between elements, so that the elements in a collection are arranged according to the classification of hash function.

When introducing some collections, we always emphasize the need to override the equlas() method and hashCode() method of a class to ensure uniqueness. The hashCode () here represents the unique identifier of the current object. The process of calculating hashCode is called hash.

1.2 why there should be Hash

We usually use arrays or linked lists to store elements. Once there is a large amount of content stored, it takes up a lot of space. In the process of finding out whether an element exists, arrays and linked lists need to be compared one by one, while hash calculation can greatly reduce the number of comparisons.

1.3 for example, chestnuts:

Now there are four numbers {2,5,9,13}. You need to find out if 13 exists.

1. To use array storage, you need to create new arrays new int[]{2,5,9,13}, and then write a loop to traverse the search:

int[] numbers = new int[]{2,5,9,13};
for (int i = 0; i < numbers.length; i++) {
    if (numbers[i] == 13){
        System.out.println("find it!");
        return;
    }
}

In this way, it needs to traverse 4 times to find it, and the time complexity is O(n).

2. If the hash function is used for calculation before storage, here I use a function casually:

H[key] = key % 3;

The hash values corresponding to the four numbers {2,5,9,13} are:

H[2] = 2 % 3 = 2;
H[5] = 5 % 3 = 2;
H[9] = 9 % 3 = 0;
H[13] = 13 % 3 = 1;

Then store them in the corresponding location.

When you want to find 13, just use the hash function to calculate its location, and then go to that location to see if it exists. In this case, you only need to find it once, with a time complexity of O(1).

Therefore, it can be found that hash is actually an optimization of random storage. It is classified first, and then searched according to the classification of this object.
Hash greatly reduces the search range through one calculation, which is naturally faster than searching from all data.
For example, you and I are a Book scalper. There are a lot of books at home. If the books are stored on the shelf (array storage) without classification, you may need to turn your head from left to right for several circles to find a book. If the books are stored separately according to categories, technical books, novels, literature, etc. (calculated according to a hash function), and the books are searched As long as we find it from its corresponding classification, it will be much easier.

1.4 hash function

The hash function is used to calculate the hash.

Hash function is a kind of mapping relation. According to the key word of data, through certain function relation, the function of storage location of the element is calculated.

Expressed as:

address = H [key]

Check the implementation of hash function: hash function

1.5 features of hash function:

• 1) Hash can be used for any size of data block;
• (2)hash can accept any length of information and output it as a fixed length message digest;
• (3) One way. Given an input M, there must be an H corresponding to it, which satisfies H(M)=h, otherwise, it is not possible, and the algorithm operation is irreversible.
• (4) Collision resistance. Given a m, it is impossible to find a m 'that is not H(M)=H(M'). That is to say, two different inputs cannot be found at the same time to make the output completely consistent.
• (5) Low complexity: the algorithm has low complexity of operation.

1.6 common functions of hash table

Code:

//The complexity of adding, deleting, modifying and querying hash table is similar to O(1), but it should be O(log5N and so on)
public class Code_01_HashMap {

	public static void main(String[] args) {
		HashMap<String, String> map = new HashMap<>();
		map.put("wang", "31");

		System.out.println(map.containsKey("wang"));
		System.out.println(map.containsKey("laowu"));
		System.out.println("=========================");

		System.out.println(map.get("wang"));
		System.out.println(map.get("laowu"));
		System.out.println("=========================");

		System.out.println(map.isEmpty());
		System.out.println(map.size());
		System.out.println("=========================");

		System.out.println(map.remove("wang"));
		System.out.println(map.containsKey("wang"));
		System.out.println(map.get("wang"));
		System.out.println(map.isEmpty());
		System.out.println(map.size());
		System.out.println("=========================");

		map.put("wang", "31");
		System.out.println(map.get("wang"));
		map.put("wang", "32");
		System.out.println(map.get("wang"));
		System.out.println("=========================");

		map.put("wang", "31");
		map.put("lao", "32");
		map.put("wu", "33");

		for (String key : map.keySet()) {
			System.out.println(key);
		}
		System.out.println("=========================");

		for (String values : map.values()) {
			System.out.println(values);
		}
		System.out.println("=========================");

		map.clear();
		map.put("A", "1");
		map.put("B", "2");
		map.put("C", "3");
		map.put("D", "1");
		map.put("E", "2");
		map.put("F", "3");
		map.put("G", "1");
		map.put("H", "2");
		map.put("I", "3");
		for (Entry<String, String> entry : map.entrySet()) {
			String key = entry.getKey();
			String value = entry.getValue();
			System.out.println(key + "," + value);
		}
		System.out.println("=========================");

		// you can not remove item in map when you use the iterator of map
//		 for(Entry<String,String> entry : map.entrySet()){
//			 if(!entry.getValue().equals("1")){
//				 map.remove(entry.getKey());
//			 }
//		 }

		// if you want to remove items, collect them first, then remove them by
		// this way.
		List<String> removeKeys = new ArrayList<String>();
		for (Entry<String, String> entry : map.entrySet()) {
			if (!entry.getValue().equals("1")) {
				removeKeys.add(entry.getKey());
			}
		}
		for (String removeKey : removeKeys) {
			map.remove(removeKey);
		}
		for (Entry<String, String> entry : map.entrySet()) {
			String key = entry.getKey();
			String value = entry.getValue();
			System.out.println(key + "," + value);
		}
		System.out.println("=========================");

	}

}

2. Design RandomPool structure

[Topic] design a structure, in which there are three functions as follows: insert(key): add a key to the structure, so as not to add repeatedly. delete(key): remove a key originally in the structure. getRandom(): returns any key in the structure randomly with equal probability.
[requirements] the time complexity of Insert, delete and getRandom methods is O(1)

public class Code_02_RandomPool {

	public static class Pool<K> {
		private HashMap<K, Integer> keyIndexMap;
		private HashMap<Integer, K> indexKeyMap;
		private int size;

		public Pool() {
			this.keyIndexMap = new HashMap<K, Integer>();
			this.indexKeyMap = new HashMap<Integer, K>();
			this.size = 0;
		}

		public void insert(K key) {
			if (!this.keyIndexMap.containsKey(key)) {
				this.keyIndexMap.put(key, this.size);
				this.indexKeyMap.put(this.size++, key);
			}
		}

		public void delete(K key) {
		//Delete the key at the specified location and complete the hole
			if (this.keyIndexMap.containsKey(key)) {
				int deleteIndex = this.keyIndexMap.get(key);
				int lastIndex = --this.size;
				K lastKey = this.indexKeyMap.get(lastIndex);
				this.keyIndexMap.put(lastKey, deleteIndex);
				this.indexKeyMap.put(deleteIndex, lastKey);
				this.keyIndexMap.remove(key);
				this.indexKeyMap.remove(lastIndex);
			}
		}

		public K getRandom() {
			if (this.size == 0) {
				return null;
			}
			int randomIndex = (int) (Math.random() * this.size); // 0 ~ size -1
			return this.indexKeyMap.get(randomIndex);
		}

	}

	public static void main(String[] args) {
		Pool<String> pool = new Pool<String>();
		pool.insert("zuo");
		pool.insert("cheng");
		pool.insert("yun");
		System.out.println(pool.getRandom());
		System.out.println(pool.getRandom());
		System.out.println(pool.getRandom());
		System.out.println(pool.getRandom());
		System.out.println(pool.getRandom());
		System.out.println(pool.getRandom());
	}
}

3. Know the bloon filter

3.1 meaning of bloon filter:

3.2 why use the bloon filter?

HashMap's question: before we talk about the principle of the bloom filter, let's think about what you usually use to judge whether an element exists? Many people should answer HashMap. It can map the value to the Key of HashMap, and then return the result within the time complexity of O(1), which is extremely efficient. However, the implementation of HashMap also has disadvantages, such as high storage capacity, considering the existence of load factor, usually the space cannot be used up, and once your value is many, such as hundreds of millions, the memory size occupied by HashMap becomes very considerable.

For example, when your data set is stored on a remote server, and the local service accepts input, and the data set is very large and it is impossible to read it into memory once to build a HashMap, there will also be problems.

In fact, bloom filter is widely used in blacklist system, spam filter system, crawler's URL weight determination system and cache penetration problem. It is known that the function of the bloom filter is to retrieve whether an element is in the collection. Some people may think that this function is very simple. It is better to query directly in redis or database. Or when the amount of data is small and the memory is large enough, it is better to use structures such as hashMap or hashSet. But if the amount of data is large, billions or more, memory can't be loaded and database retrieval is very slow, how should we deal with it? At this time, we may consider the bloom filter, because it is an algorithm with little space efficiency and very fast query time, but the business needs to be able to bear a misjudgment rate.

3.3 hash function

Properties of hash function:

1. Classical hash functions have an infinite range of input values (infinity).
2. The output fields of classical hash functions are all fixed ranges (finite, assuming the output field is S)
3. When the same value is passed to the hash function, the return value must be the same
4. When different input values are passed to the hash function, the return values may be the same or different.
5. The input values are distributed as evenly as possible on S

The first three points are the basis of the hash function. The fourth point describes the hash collision phenomenon of the hash function. Because the input field is infinite and the output field is finite, it is inevitable that there will be different values in the input field corresponding to the input field S. The fifth thing is the key to evaluate a hash function. The better the hash function is, the more uniform the distribution will be and it has nothing to do with the rule of the input value. For example, there are "hash1", "hash2" and "hash3" input values that are similar. The result of hash function calculation should be very different, which can be verified by common MD5 and SHA1 algorithms. If an excellent function can achieve the return value of different input values can be evenly distributed in S, and its return value is redundant to m (% m), the return value can be considered to be evenly distributed in the 0~m-1 position.

3.4 based on cache business analysis, the principle of bloon filter

In most applications, when a request is sent in the business system, it will first query from the cache; if it exists in the cache, it will return directly; if it does not exist in the return, it will query the database. The process is as follows: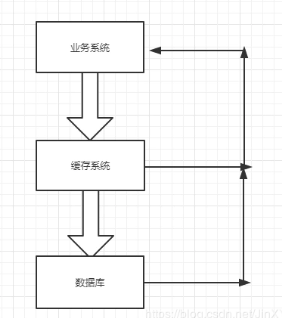

Cache penetration: when requesting data that does not exist in the database, all requests will hit the database, which is called cache penetration. If there are more requests, it will seriously waste database resources and even lead to database feign death.

The next step is to introduce the bloon filter. There is a bit array of length m, as we know, each position only occupies one bit, each position only has two states of 0 and 1. Suppose there are k hash functions that are independent of each other, and the input fields are s and greater than or equal to M. Every result calculated is redundant to m, and then the corresponding position is set to 1 (black) on the bit array, as shown in the following figure: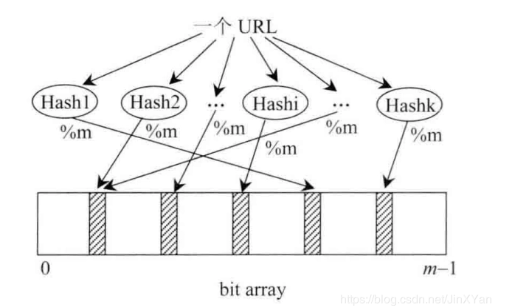

At this point, the impact of an input object on the bit array set is over. We can see that multiple positions will be blacked, that is, set to 1. Then all the input objects are described as black arrays in this way, and finally a bloom filter is generated, which represents the collection of all the input objects.
So how to judge whether an object is in the filter? Suppose an input object is hash1, we need to calculate K values by looking at k hash functions, and then we can get k [0,m-1] values by taking K values as the remainder (% m). Then we determine whether all the k values on bit array are black. If one of them is not black, then it is certain that hash1 is not in this set. If it is all black, it means that hash1 is in the set, but it may be misjudged. Because when there are too many input objects and the set is too small, most of the positions in the set will be blacked out. When checking the hash1, it is possible that the corresponding K positions of the hash1 are blacked out, and then it is wrongly believed that the hash1 exists in the set.
Example: add 30000 to the bloom filter. The bottom layer is an array of type int, with a length of 1000.

• 30000 means that the 30000 bit in the array is blacked out, not the actual number.
• The array length is 1000, which can hold 32 * 1000 bit s in total.

3.5 control the misjudgment rate of bloon filter

If the size m of the bit array set is too small compared with the number of input objects, the error rate will be higher. In this paper, a proven formula is directly introduced. According to the number of input objects n and the error rate we want to achieve p, the size m of the bloon filter and the number k of the hash function are calculated
The size m formula of bloon filter: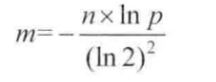

The number k formula of hash function: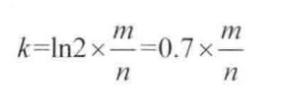

The true error rate p formula of bloon filter: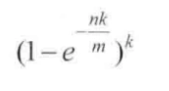

Suppose our caching system, key is userId, value is user. If we have 1 billion users, the specified error rate cannot exceed 0.01%. By calculating with a calculator, we can get m=19.17n, round up to 20n, that is to say, 20 billion bit s are needed. After conversion, the required memory size is 2.3G. Through the second formula, we can calculate the required hash function k=14. Because the round up is used in the calculation of M, the true error rate is absolutely less than or equal to 0.01%.
More concepts: Bloom filter

3.6 implementation of bloon filter

public class BloomFilter {


    /**
     * bitSet Size
     */
    private static final int DEFAULT_SIZE = 2 << 24;
    /**
     * Selected hash function
     */
    private static final int[] SEEDS = new int[]{3, 13, 46, 71, 91, 134};

    /**
     * bitSet Each bit can only be true or false, which is actually the 0 or 1 of bit array
     */
    private BitSet bits = new BitSet(DEFAULT_SIZE);
    private SimpleHash[] func = new SimpleHash[SEEDS.length];

    public static void main(String[] args) {
        String value = "wxwwt@gmail.com";
        BloomFilter filter = new BloomFilter();
        System.out.println(filter.contains(value));
        filter.add(value);
        System.out.println(filter.contains(value));
    }

    public BloomFilter() {
        for (int i = 0; i < SEEDS.length; i++) {
            func[i] = new SimpleHash(DEFAULT_SIZE, SEEDS[i]);
        }
    }

    public void add(String value) {
        for (SimpleHash f : func) {
            bits.set(f.hash(value), true);
        }
    }

    public boolean contains(String value) {
        if (value == null) {
            return false;
        }
        boolean ret = true;
        for (SimpleHash f : func) {
            ret = ret && bits.get(f.hash(value));
        }
        return ret;
    }

    public static class SimpleHash {

        private int cap;
        private int seed;

        public SimpleHash(int cap, int seed) {
            this.cap = cap;
            this.seed = seed;
        }

        /**
         * Calculate hash value
         *
         * @param value
         * @return
         */

        public int hash(String value) {
            int result = 0;
            int len = value.length();
            for (int i = 0; i < len; i++) {
                result = seed * result + value.charAt(i);
            }
            return (cap - 1) & result;
        }

    }
}

In fact, it is more often to use the bloon filter implemented in Google (guava).

3.4 use scenario of Bloom filter

1. The web crawler can judge whether the current url has been crawled through the bloom filter;

2. To prevent malicious links or spam, SMS, etc., judge the link from billions of links or spam (email sender, SMS sender is in the blacklist or not),
Usually, the call prompt on the mobile phone says malicious promotion and take away. This kind of scene can also be judged by the bloom filter;

3. To prevent cache breakdown, put the existing cache in the bloom. When using the cache, you can access the bloom filter first, and access the cache if it exists, and access the database if it does not exist;

4. The retrieval system can query whether the current input information exists in the database, or use the bloom filter.

4. Recognize the consistency hash (server compression / load balancing)

For details, Consistent Hashing

5. Islands issue

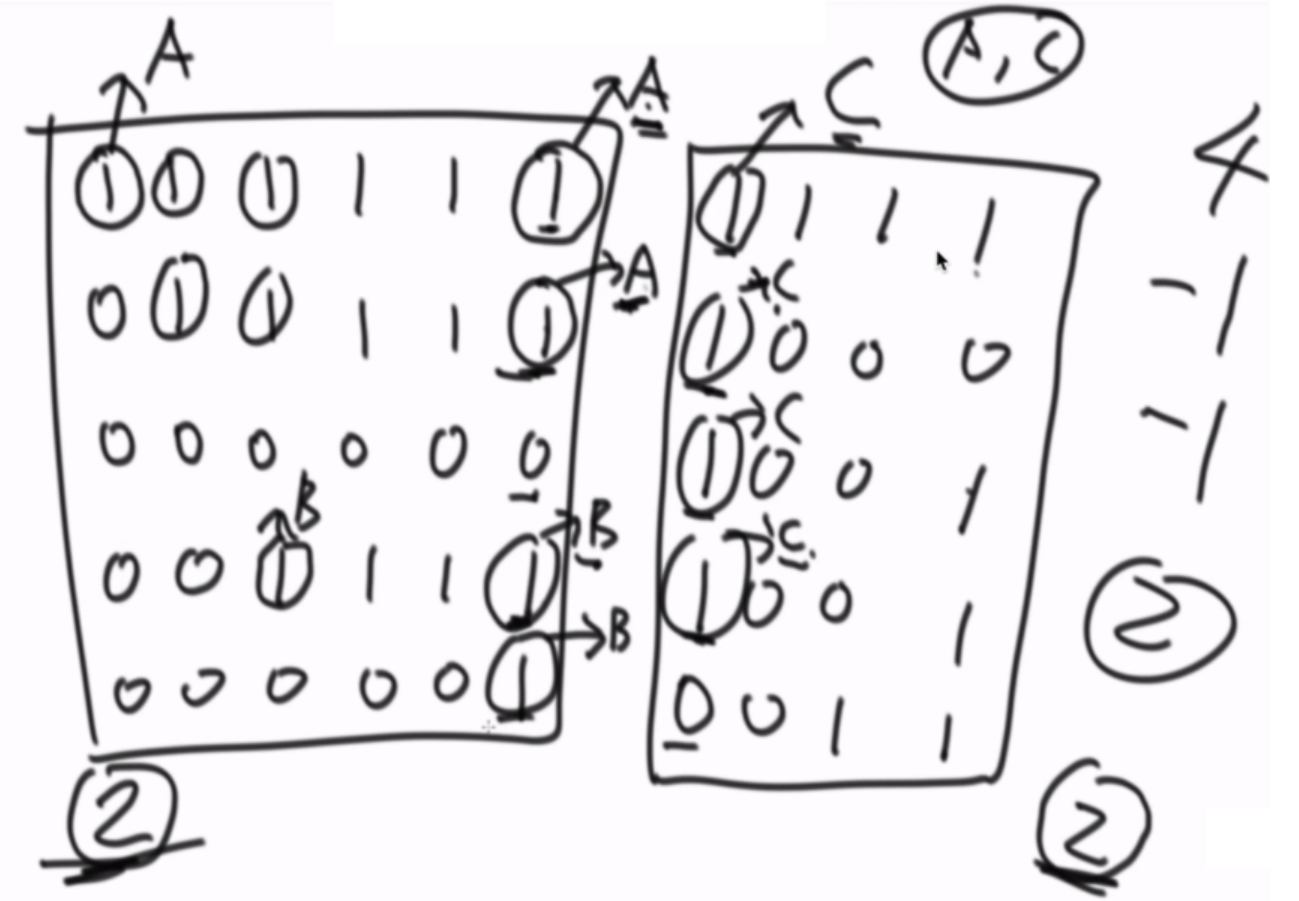
There are only two values of 0 and 1 in a matrix. Each position can be connected with its own top, bottom, left and right positions. If a piece of 1 is connected together, this part is called an island. How many islands are there in a matrix?
Give an example:

There are three islands in this matrix.
First of all, I think: use the classic recursive method to solve:

public class Code_03_Islands {

	public static int countIslands(int[][] m) {
		if (m == null || m[0] == null) {
			return 0;
		}
		int N = m.length;//That's ok
		int M = m[0].length;//column
		int res = 0;
		for (int i = 0; i < N; i++) {
			for (int j = 0; j < M; j++) {
				if (m[i][j] == 1) {
					res++;
					infect(m, i, j, N, M);//Infection function
				}
			}
		}
		return res;
	}

	public static void infect(int[][] m, int i, int j, int N, int M) {//This recursion will continue to execute, and will terminate only when the return condition below is met
		if (i < 0 || i >= N || j < 0 || j >= M || m[i][j] != 1) {//As long as the row or column is less than 0, greater than the boundary, or the value is not equal to 1, return directly
			return;
		}
		m[i][j] = 2;//Number of infections set to 2
		infect(m, i + 1, j, N, M);//Number on the previous line of the current number of infections
		infect(m, i - 1, j, N, M);//Infect the number of the next line of the current number
		infect(m, i, j + 1, N, M);//The number in the right row of the current number of infections
		infect(m, i, j - 1, N, M);//The left row of the current number of infections
	}

	public static void main(String[] args) {
		int[][] m1 = {  { 0, 0, 0, 0, 0, 0, 0, 0, 0 }, 
				        { 0, 1, 1, 1, 0, 1, 1, 1, 0 }, 
				        { 0, 1, 1, 1, 0, 0, 0, 1, 0 },
				        { 0, 1, 1, 0, 0, 0, 0, 0, 0 }, 
				        { 0, 0, 0, 0, 0, 1, 1, 0, 0 }, 
				        { 0, 0, 0, 0, 1, 1, 1, 0, 0 },
				        { 0, 0, 0, 0, 0, 0, 0, 0, 0 }, };
		System.out.println(countIslands(m1));//3

		int[][] m2 = {  { 0, 0, 0, 0, 0, 0, 0, 0, 0 }, 
						{ 0, 1, 1, 1, 1, 1, 1, 1, 0 }, 
						{ 0, 1, 1, 1, 0, 0, 0, 1, 0 },
						{ 0, 1, 1, 0, 0, 0, 1, 1, 0 }, 
						{ 0, 0, 0, 0, 0, 1, 1, 0, 0 }, 
						{ 0, 0, 0, 0, 1, 1, 1, 0, 0 },
						{ 0, 0, 0, 0, 0, 0, 0, 0, 0 }, };
		System.out.println(countIslands(m2));//1

	}

}

If for a super large matrix, we can use the division method of the lower edge to think about it, and use the algorithm idea of parallel search set to solve it...

6. Understand and check the structure

A fool can read it and check it