This paper is mainly about the realization of some algorithms and scattered algorithm knowledge about binary tree involved in the previous two articles. It is difficult to run through some knowledge algorithms of binary tree. Simple implementation of binary tree helps to understand the meaning of algorithm and deepen the impression

For the previous algorithm description, see:
Algorithms for calculating the number, depth, total number of nodes and replication of binary trees with 0, 1 and 2 nodes
First, middle and last traversal of binary tree

The following is the algorithm implementation result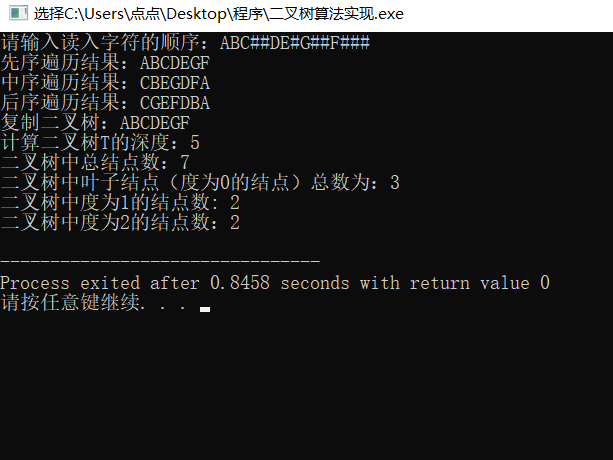

The specific code is as follows:

#include<iostream>
using namespace std;
typedef struct BiTNode{
	 char data;
	 struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

//Traversal to create binary tree
void CreateBiTree(BiTree &T)
{
	 char ch; 
	 cin>>ch;
	 if(ch=='#')
	  T=NULL;
	 else
	 {
		  T=new BiTNode;//Generate root
		  T->data=ch;//Set the root data field to ch
		  CreateBiTree(T->lchild);//Recursively create left subtree
		  CreateBiTree(T->rchild);//Recursively create right subtree
	 }//If void type is not used, return value must be written, such as return OK,return true, etc
	}//CreateBiTree 
	
//Preorder traversal
void PreOrderTraverse(BiTree T)
{
	 if(T==NULL)
	  return ;
	 else
	  {
	   cout<<T->data;
	   PreOrderTraverse(T->lchild);
	   PreOrderTraverse(T->rchild);
 	  } 
 } 
//Sequential traversal
void InOrderTraverse(BiTree T)
{
	 if(T==NULL)
	  return;
	 else
	 {
	 	 InOrderTraverse(T->lchild);
 		 cout <<T->data;
  		 InOrderTraverse(T->rchild);
 }
}

//Post order traversal
void PostOrderTraverse(BiTree T)
{
	 if(T==NULL)
	  return;
	 else
	 {
	  PostOrderTraverse(T->lchild);
	  PostOrderTraverse(T->rchild);
	  cout <<T->data;
	 }
}
	
//Duplicate binary tree
int Copy(BiTree T,BiTree &NewT)
{
	 if(T==NULL)//If it is an empty tree, the recursion ends
	 {
	  NewT=NULL;
	  return 0;
	 }
	 else
	 {
		  NewT=new BiTNode;
		  NewT->data=T->data;//Copy root
		  Copy(T->lchild,NewT->lchild);//Recursively copy left subtree
		  Copy(T->rchild,NewT->rchild);//Recursively copy right subtree
	}	  
 }

//Calculating the depth of a binary tree 
int Depth(BiTree T)
{
	 int m,n;
	 if(T==NULL)
	  return 0;//If it is an empty tree, return the depth 0, and the recursion ends
	 else
	 {
		  m=Depth(T->lchild);//The depth of recursive left subtree is recorded as m
		  n=Depth(T->rchild);//The depth of recursive right subtree is n
		  if(m>n)
			 return (m+1);
		  else
		   return (n+1); 
		 }// The depth of binary tree is the greater of m and n + 1
		}
		
//Calculate the total number of nodes in binary tree
int NodeCount(BiTree T)
{
	 if(T==NULL)
	  return 0;
	 else
	  return NodeCount(T->lchild)+NodeCount(T->rchild)+1; 
}

// Calculate the total number of leaf nodes (degree 0) of binary tree 
int LeafCount(BiTree T)
{
	 if(T==NULL)//Return 0 if tree is empty
	  return 0;
	 if(T->lchild==NULL && T->rchild==NULL)
	  return 1;//If it is a leaf node, return 1 
	 else
	  return  LeafCount(T->lchild)+LeafCount(T->rchild);
}//Total number of leaf nodes

//Number of nodes with degree 1 
int oneCount(BiTree T)
{
	 int i=0;
	 if(T==NULL)//Return 0 if tree is empty
	  return 0;
	  if((T->lchild!=NULL&&T->rchild==NULL)||(T->lchild==NULL&&T->rchild!=NULL))
	  return 1+oneCount(T->lchild)+oneCount(T->rchild); 
	  else 
	  return oneCount(T->lchild)+oneCount(T->rchild);
}

//Number of nodes with degree 2
 int twoCount(BiTree T)
{
	 int i=0;
	 if(T==NULL)//Return 0 if tree is empty
	  return 0;
	if(T->lchild!=NULL && T->rchild!=NULL)
	  return 1+twoCount(T->lchild)+twoCount(T->rchild); 
	 else 
	  return twoCount(T->lchild)+twoCount(T->rchild);
}

int main()
{
	 BiTree T,F;
	 
	 cout<<"Please enter the order in which the characters are read:";
	 //Test case: ABC × de × g × f###
	 CreateBiTree(T);
	
	 cout<<"First order traversal result:";
	 PreOrderTraverse(T);
	 cout<<endl;
	 
	 cout<<"Middle order traversal result:";
	 InOrderTraverse(T);
	 cout<<endl;
	 
	 cout<<"Subsequent traversal results:";
	 PostOrderTraverse(T);
	 cout<<endl;
	 
	 cout<<"Copy binary tree:";
	 Copy(T,F);
	 PreOrderTraverse(F);//Preorder traversal 
	 cout<<endl;
	 
	 cout<<"Compute binary tree T Depth:";
	 cout<<Depth(T)<<endl;
	 
	 cout<<"Sum points in binary tree:";
	 cout<<NodeCount(T)<<endl;
	 
	 cout<<"The total number of leaf nodes (nodes with degree 0) in a binary tree is:";
	 cout<<LeafCount(T)<<endl;
	 
	 cout<<"Node number of 1 in binary tree: "; 
	 cout<<oneCount(T)<<endl;
	 
	 cout<<"The number of nodes in a binary tree is 2";
	 cout<<twoCount(T)<<endl; 
	 return 0;
}		

Let's have a good look at it