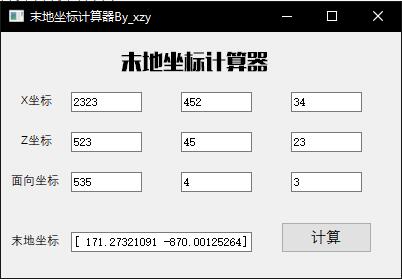
I. brief introduction
For Minecraft players, it is undoubtedly a more painful process to find the terminal fortress. The generation of the terminal fortress is usually a certain distance from the birth point of the player, so in general, it needs to consume a large number of rare terminal pearl to indicate the direction, which greatly slows down the clearance speed of the player and reduces the game experience. In fact, through the characteristics of the last shadow pearl pointing to the end of the earth, correct use and simple mathematical calculation, we can use 1-3 last shadow pearls to relatively accurately locate the end of the earth coordinates, thus simplifying the process.
2, Principle overview
This calculator uses a very simple mathematical model. Theoretically, the coordinates can be calculated when two straight lines intersect at one point. However, due to certain errors in visual coordinates, the triangle enclosed by three straight lines (see Figure 1) is used here, and then the triangle center (the center of gravity is used for the simplified calculation) is taken to reduce the errors.
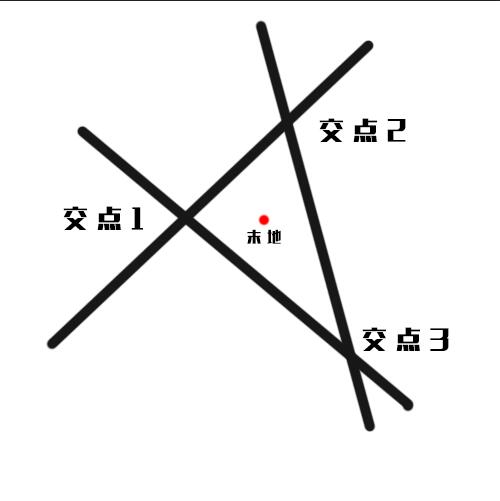 Sketch 1
Sketch 1
Record the X, Z and f coordinates in the game, and establish the coordinate system. Note that when f is 0 degrees in the game, it is the positive direction of Z axis, and when - 90 degrees, it is the negative direction of X axis. Consider taking the angle of F as negative, taking Z as the horizontal axis and X as the vertical axis to establish the Cartesian coordinate system. (see sketch 2)
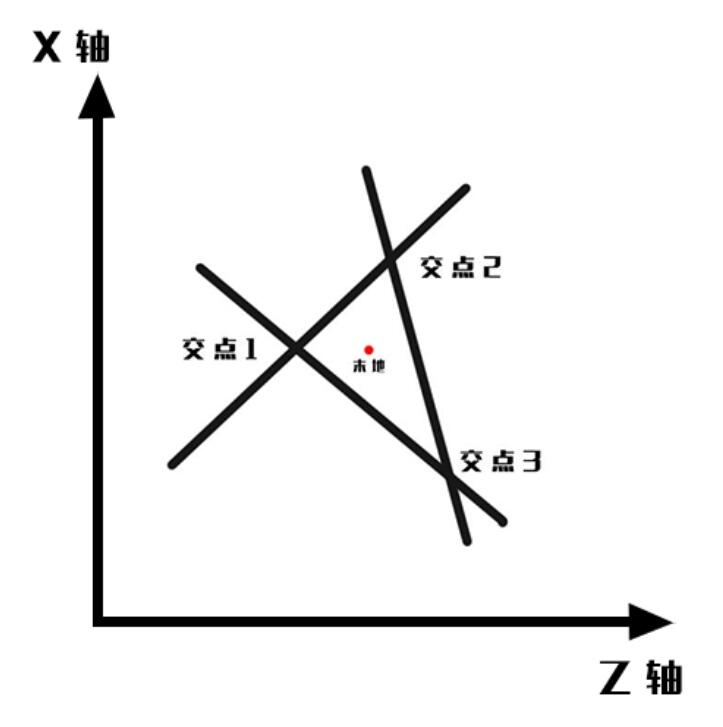 Sketch 2
Sketch 2
Set the recorded coordinate point as point 1: (a1,b1), point 2: (a2,b2), point 3: (a3,b3)
There are three sets of linear equations about X,Z, X-kZ=b-ak (where k = tan(radians(-f)))
Solve the system of linear equations and get the coordinates of the three intersections, which are recorded as ABC.
Terminal coordinate D ≈ (A+B+C)/3
3, Implementation method
First, use python to implement the code.
Use numpy to solve linear equations.
import numpy as np
import math
# number=input("input point coordinate number")
x=[];y=[];face=[];A=[];b=[];k=[];r=[]
# for i in range(0,int(number)):
for i in range(0,3):
y.append(input("Please input X coordinate:\n"))
x.append(input("Please input Z coordinate:\n"))
face.append(input("Please enter coordinate facing:\n"))
k.append(math.tan(math.radians(-1*float(face[i]))))
# for i in range(0,int(number)):
for i in range(0,2):
A=[[1,-k[i]],[1,-k[i+1]]]
b=[(float(y[i])-float(x[i])*k[i]),(float(y[i+1])-float(x[i+1])*k[i+1])]
# print("x[i]:",x[i],"\n","y[i]:",y[i],"\n","k[i]:",k[i],"\n")
# print("x[i+1]:",x[i+1],"\n","y[i+1]:",y[i+1],"\n","k[i+1]:",k[i+1],"\n")
# print("A:",A,"\n","b",b,"\n")
r.append(np.linalg.solve(A,b))
A=[[1,-k[0]],[1,-k[-1]]]
b=[(float(y[0])-float(x[0])*k[0]),(float(y[-1])-float(x[-1])*k[-1])]
r.append(np.linalg.solve(A,b))
result=(r[0]+r[1]+r[2])/3
print("The final coordinates are:",result,"\n")
input("Enter any key to exit!")
#print(r[0],"\n\n",r[1],"\n\n",r[2],"\n")In order to facilitate the operation and encapsulation, I further learned how to write the ui with Pyqt5 and QT designer.
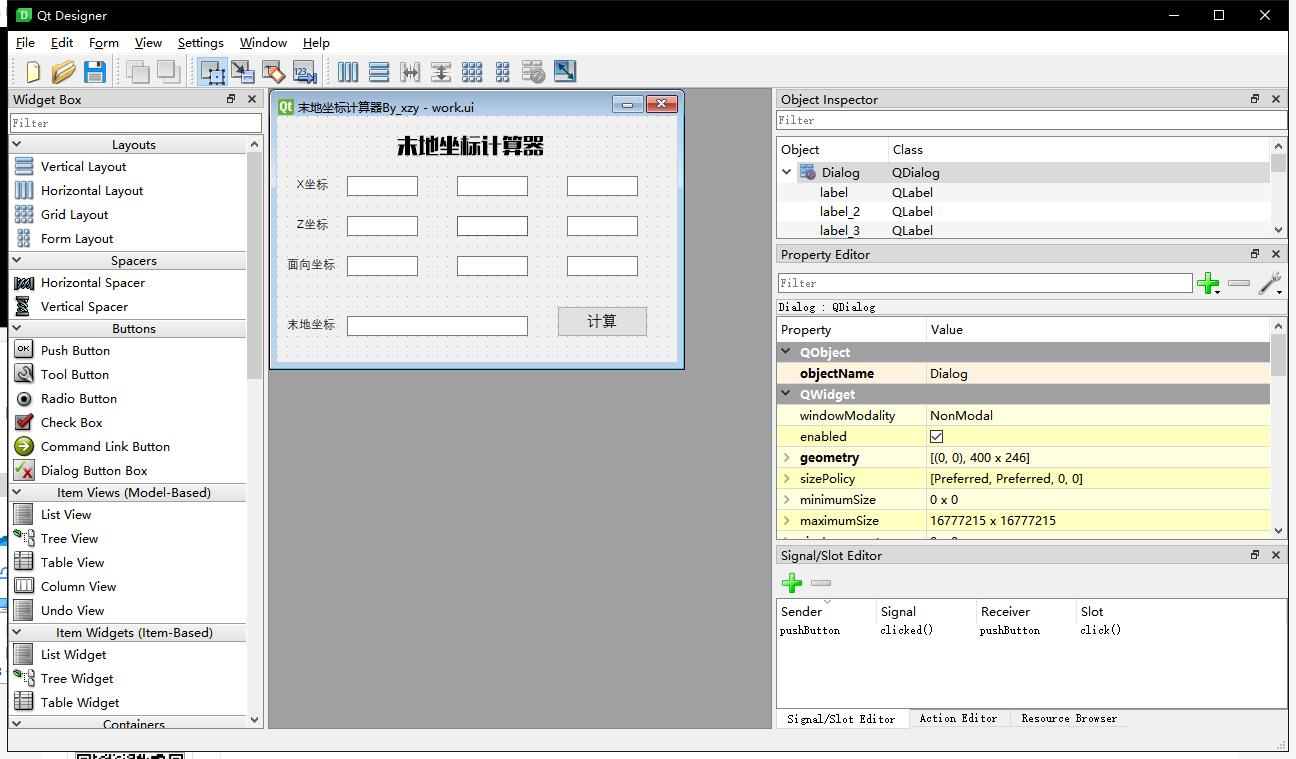
Python internal code
# -*- coding: utf-8 -*-
# Form implementation generated from reading ui file 'work.ui'
#
# Created by: PyQt5 UI code generator 5.13.0
#
# WARNING! All changes made in this file will be lost!
import sys
import numpy as np
import math
from PyQt5 import QtCore, QtGui, QtWidgets
from PyQt5.QtCore import *
from PyQt5.QtWidgets import *
from PyQt5.QtGui import *
class Ui_Dialog(object):
def setupUi(self, Dialog):
Dialog.setObjectName("Dialog")
Dialog.resize(400, 246)
self.lineEdit = QtWidgets.QLineEdit(Dialog)
self.lineEdit.setGeometry(QtCore.QRect(70, 60, 71, 20))
self.lineEdit.setObjectName("lineEdit")
self.lineEdit_2 = QtWidgets.QLineEdit(Dialog)
self.lineEdit_2.setGeometry(QtCore.QRect(180, 60, 71, 20))
self.lineEdit_2.setObjectName("lineEdit_2")
self.lineEdit_3 = QtWidgets.QLineEdit(Dialog)
self.lineEdit_3.setGeometry(QtCore.QRect(70, 100, 71, 20))
self.lineEdit_3.setObjectName("lineEdit_3")
self.lineEdit_4 = QtWidgets.QLineEdit(Dialog)
self.lineEdit_4.setGeometry(QtCore.QRect(290, 60, 71, 20))
self.lineEdit_4.setObjectName("lineEdit_4")
self.lineEdit_5 = QtWidgets.QLineEdit(Dialog)
self.lineEdit_5.setGeometry(QtCore.QRect(180, 100, 71, 20))
self.lineEdit_5.setObjectName("lineEdit_5")
self.lineEdit_6 = QtWidgets.QLineEdit(Dialog)
self.lineEdit_6.setGeometry(QtCore.QRect(290, 100, 71, 20))
self.lineEdit_6.setObjectName("lineEdit_6")
self.lineEdit_7 = QtWidgets.QLineEdit(Dialog)
self.lineEdit_7.setGeometry(QtCore.QRect(290, 140, 71, 20))
self.lineEdit_7.setObjectName("lineEdit_7")
self.lineEdit_8 = QtWidgets.QLineEdit(Dialog)
self.lineEdit_8.setGeometry(QtCore.QRect(180, 140, 71, 20))
self.lineEdit_8.setObjectName("lineEdit_8")
self.lineEdit_9 = QtWidgets.QLineEdit(Dialog)
self.lineEdit_9.setGeometry(QtCore.QRect(70, 140, 71, 20))
self.lineEdit_9.setObjectName("lineEdit_9")
self.label = QtWidgets.QLabel(Dialog)
self.label.setGeometry(QtCore.QRect(20, 60, 41, 16))
font = QtGui.QFont()
font.setFamily("Equal line")
self.label.setFont(font)
self.label.setObjectName("label")
self.label_2 = QtWidgets.QLabel(Dialog)
self.label_2.setGeometry(QtCore.QRect(20, 100, 41, 16))
font = QtGui.QFont()
font.setFamily("Equal line")
self.label_2.setFont(font)
self.label_2.setObjectName("label_2")
self.label_3 = QtWidgets.QLabel(Dialog)
self.label_3.setGeometry(QtCore.QRect(10, 140, 51, 16))
font = QtGui.QFont()
font.setFamily("Equal line")
self.label_3.setFont(font)
self.label_3.setObjectName("label_3")
self.label_4 = QtWidgets.QLabel(Dialog)
self.label_4.setGeometry(QtCore.QRect(120, 0, 161, 61))
font = QtGui.QFont()
font.setFamily("Lettering workshop force black (non-commercial) conventional")
font.setPointSize(16)
self.label_4.setFont(font)
self.label_4.setObjectName("label_4")
self.pushButton = QtWidgets.QPushButton(Dialog)
self.pushButton.setGeometry(QtCore.QRect(280, 190, 91, 31))
font = QtGui.QFont()
font.setFamily("Equal line")
font.setPointSize(11)
self.pushButton.setFont(font)
self.pushButton.setObjectName("pushButton")
self.lineEdit_10 = QtWidgets.QLineEdit(Dialog)
self.lineEdit_10.setGeometry(QtCore.QRect(70, 200, 181, 20))
self.lineEdit_10.setObjectName("lineEdit_10")
self.label_5 = QtWidgets.QLabel(Dialog)
self.label_5.setGeometry(QtCore.QRect(10, 200, 51, 16))
font = QtGui.QFont()
font.setFamily("Equal line")
self.label_5.setFont(font)
self.label_5.setObjectName("label_5")
self.lineEdit_10.setReadOnly(True)
self.pushButton.clicked.connect(self.clickbtn)
self.retranslateUi(Dialog)
QtCore.QMetaObject.connectSlotsByName(Dialog)
Dialog.show()
def retranslateUi(self, Dialog):
_translate = QtCore.QCoreApplication.translate
Dialog.setWindowTitle(_translate("Dialog", "Terminal coordinate calculator By_xzy"))
self.label.setText(_translate("Dialog", "X coordinate"))
self.label_2.setText(_translate("Dialog", "Z coordinate"))
self.label_3.setText(_translate("Dialog", "Coordinate oriented"))
self.label_4.setText(_translate("Dialog", "Terminal coordinate calculator"))
self.pushButton.setText(_translate("Dialog", "Calculation"))
self.label_5.setText(_translate("Dialog", "Final coordinates"))
Dialog.show()
def clickbtn(self):
x=[self.lineEdit_3.text(),self.lineEdit_5.text(),self.lineEdit_6.text()]
y=[self.lineEdit.text(),self.lineEdit_2.text(),self.lineEdit_4.text()]
face=[self.lineEdit_9.text(),self.lineEdit_8.text(),self.lineEdit_7.text()]
k=[math.tan(math.radians(-1*float(face[0]))),math.tan(math.radians(-1*float(face[1]))),math.tan(math.radians(-1*float(face[2])))]
A=[];b=[];r=[]
for i in range(0,2):
A=[[1,-k[i]],[1,-k[i+1]]]
b=[(float(y[i])-float(x[i])*k[i]),(float(y[i+1])-float(x[i+1])*k[i+1])]
r.append(np.linalg.solve(A,b))
A=[[1,-k[0]],[1,-k[-1]]]
b=[(float(y[0])-float(x[0])*k[0]),(float(y[-1])-float(x[-1])*k[-1])]
r.append(np.linalg.solve(A,b))
result=(r[0]+r[1]+r[2])/3
self.lineEdit_10.setText(str(result))
if __name__ == "__main__":
app = QApplication(sys.argv)
form = QWidget()
w = Ui_Dialog()
w.setupUi(form)
form.show()
sys.exit(app.exec_())Because the interface and program are not enough, the implementation code and ui are written together.
Using pyinstaller to encapsulate tests

Test successful!
(Note: if the input is a singular matrix, the program will report an error.)
4, Game operation
For the simple operation of the players in the game, they only need to throw three last shadow pearls, and record the coordinates of the location and the coordinates of the face, but they need to follow certain operation specifications in the specific operation, otherwise they may get unexpected results.
Step 1
Throw the last shadow pearl, align the center pointer with the center of the last shadow pearl as much as possible, and record the X,Z and F coordinates. (y coordinate is not needed)
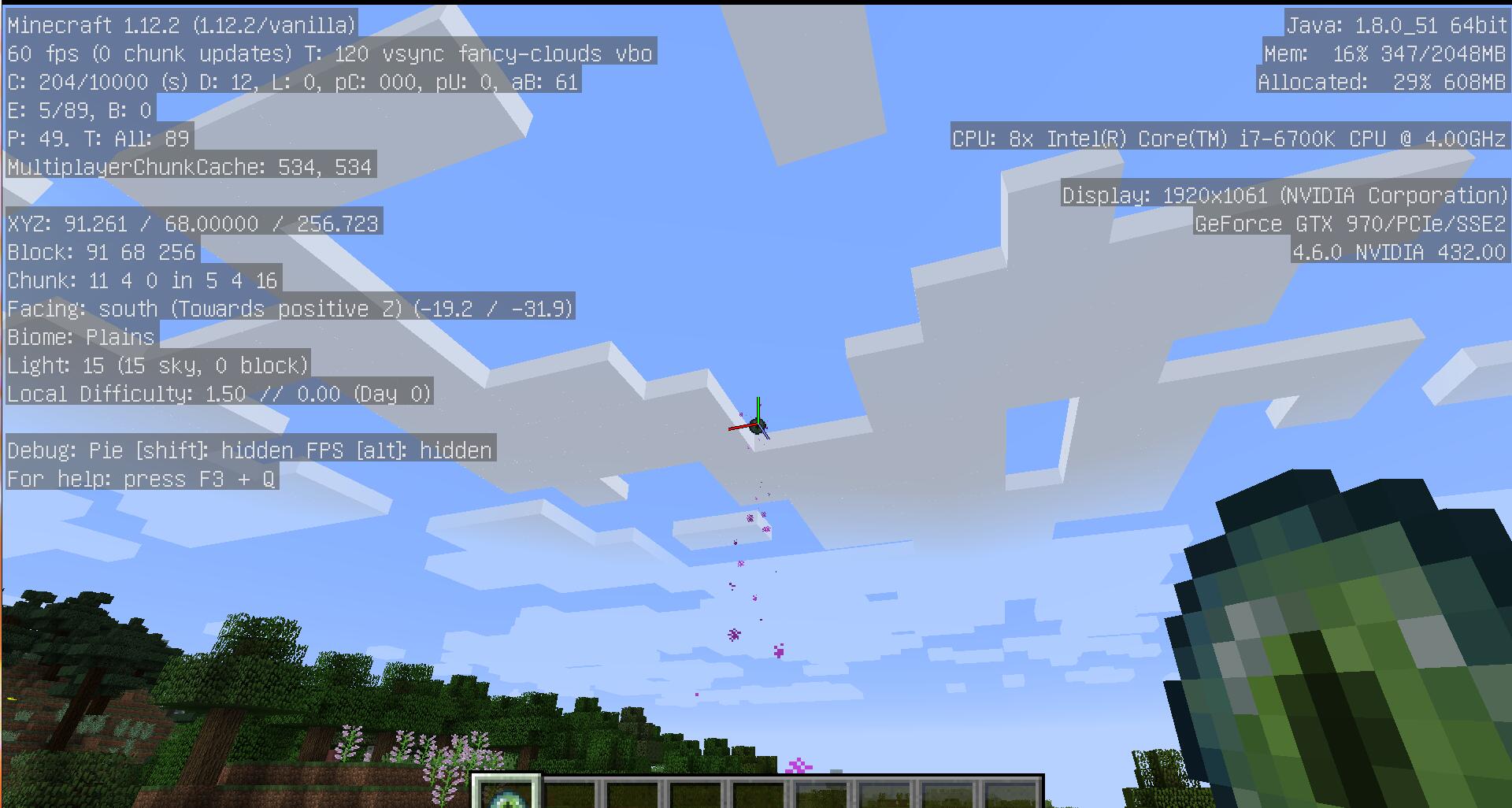
Step 2
It is about 60-150 grid away from the first pointing position of the last shadow pearl at an angle of 60-90 degrees. Be careful not to go too far, or it may be wrong to locate a different fortress.
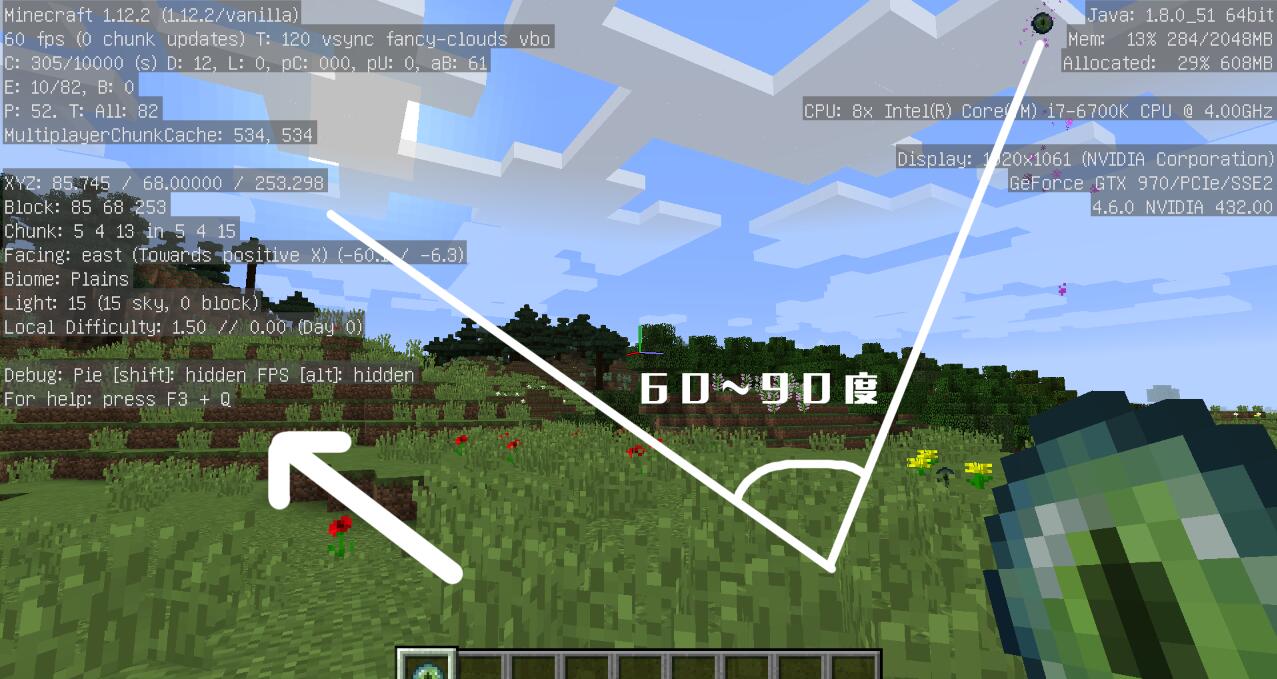
Step 3
Repeat step 1 and operate again until the coordinates are recorded 3 times.
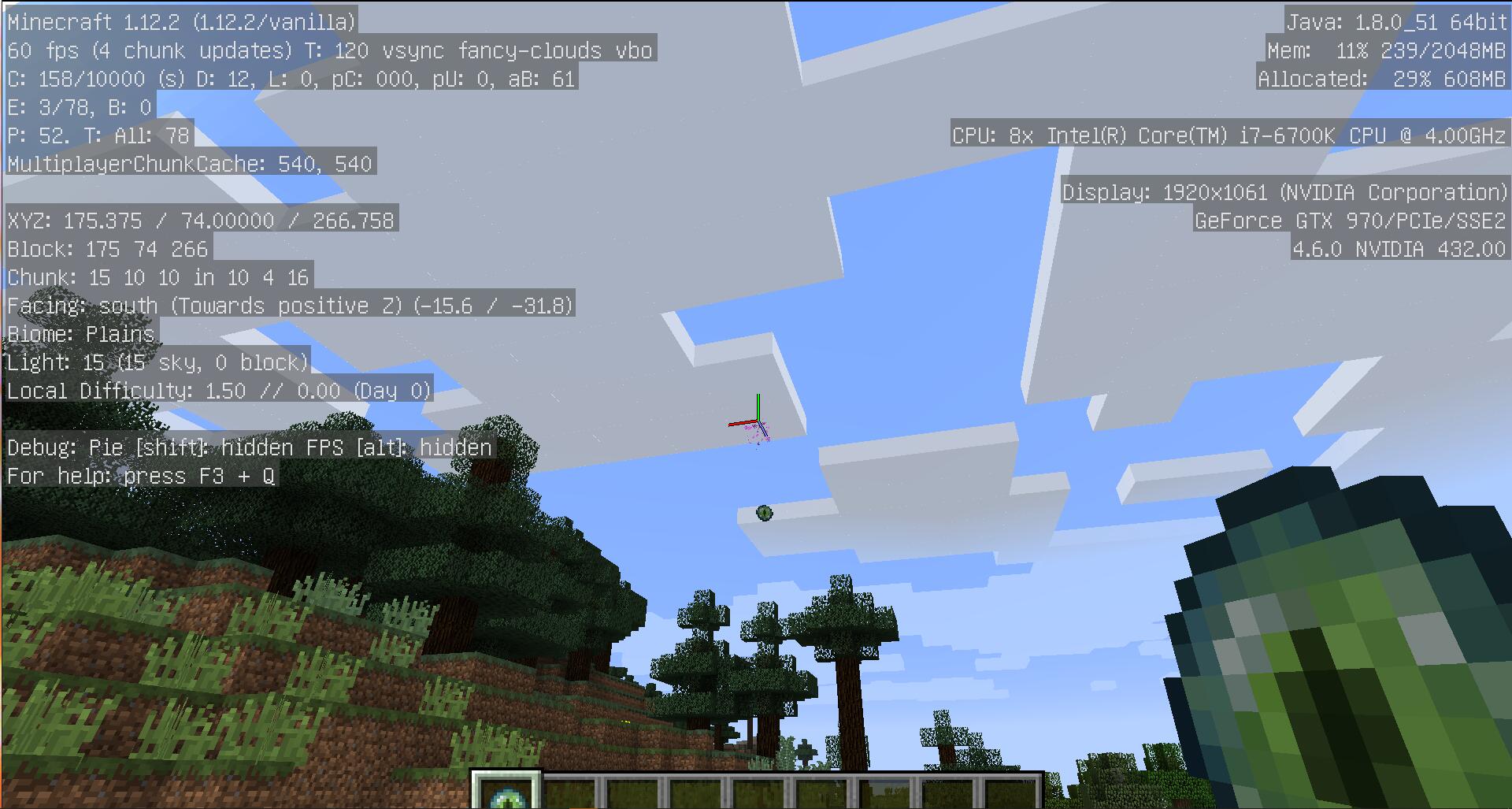
Step 4
Open the program, input the coordinates, and click calculate.
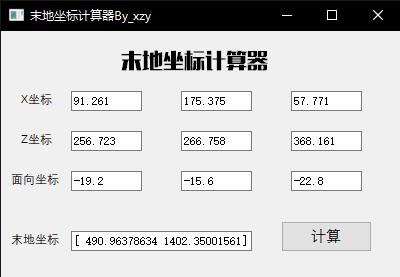
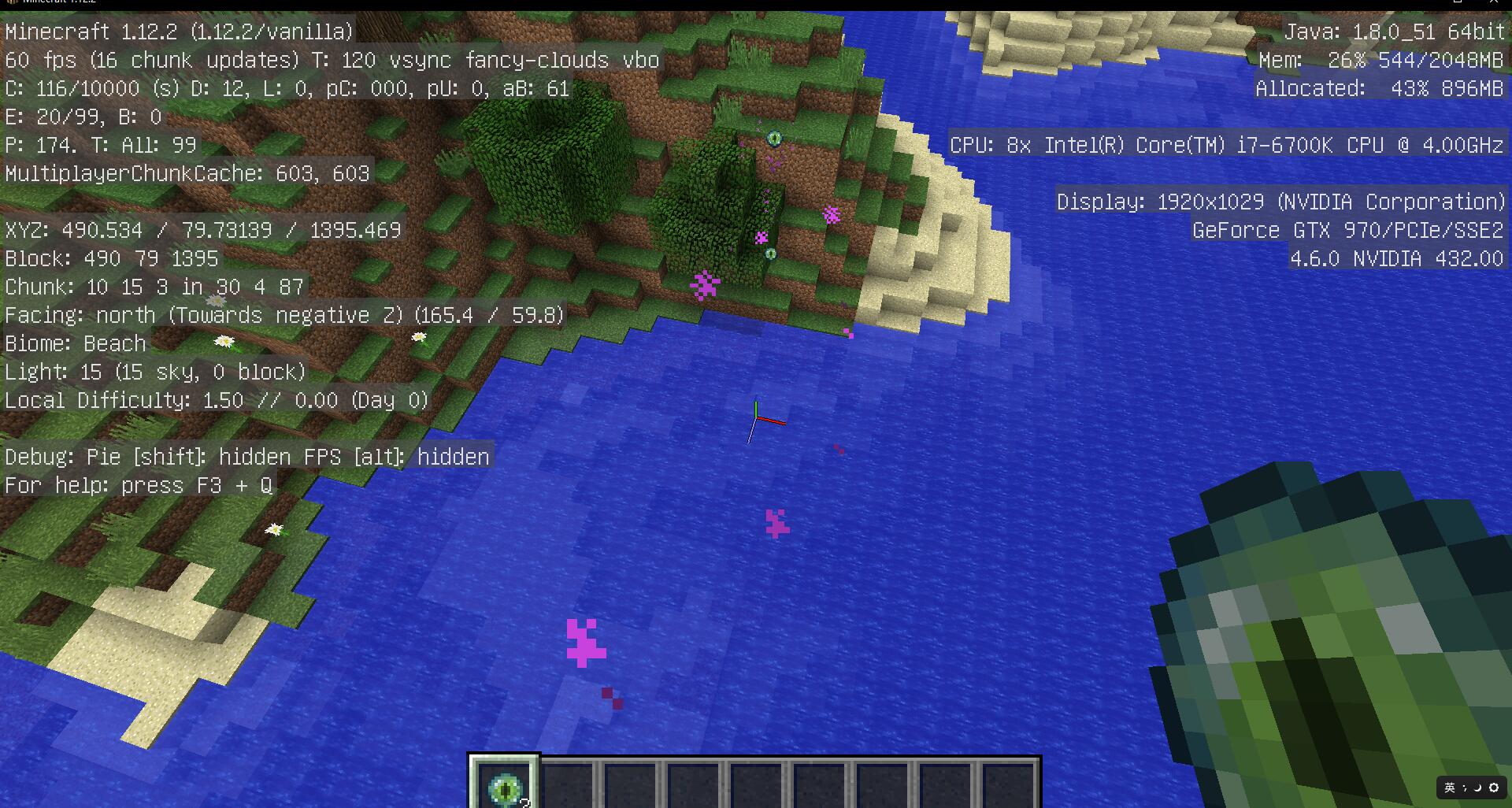
Step 5
Go to the target location and throw a pearl for verification (only for verification)
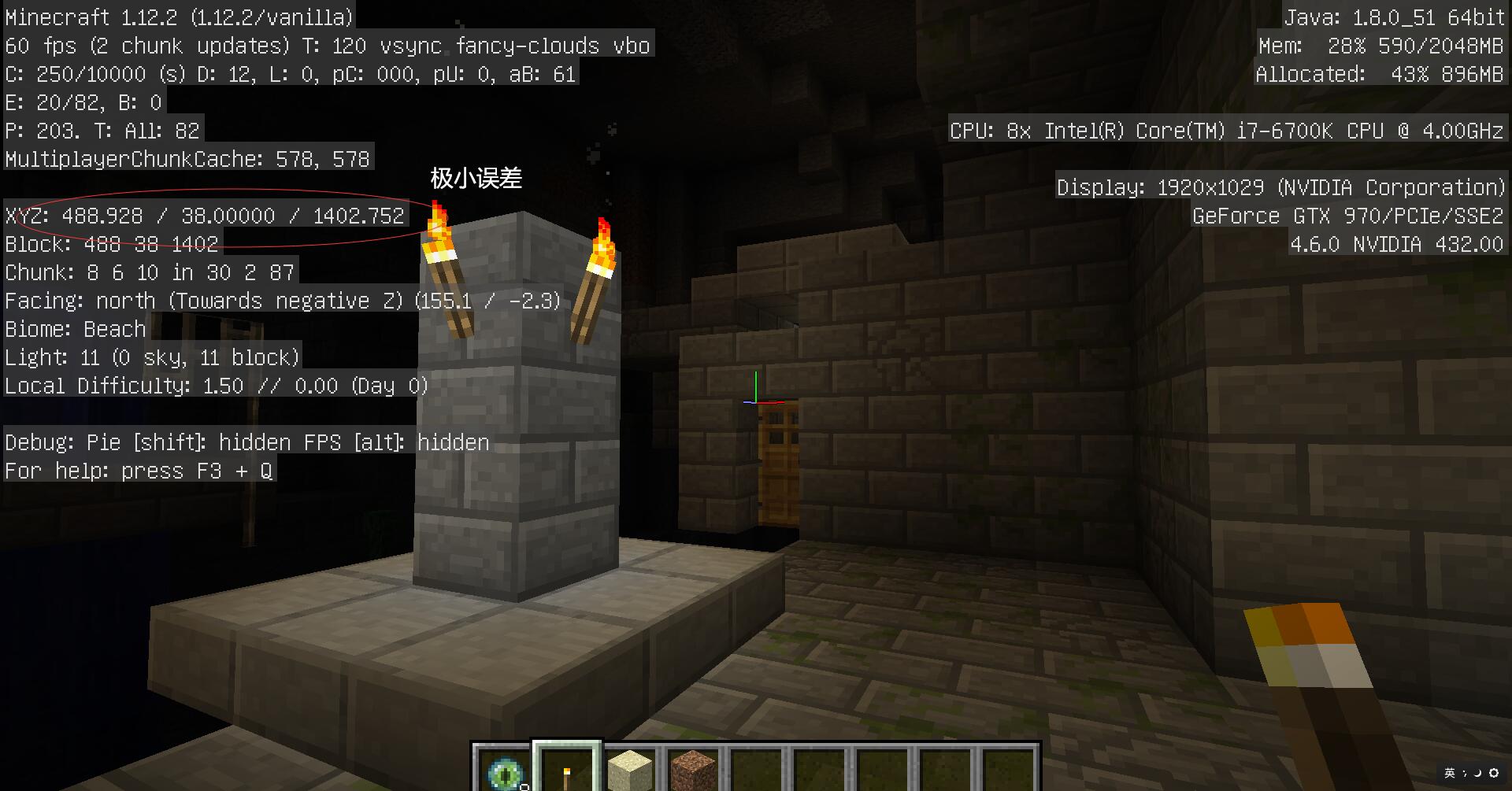
Dig down to the fortress, the error is very small!
5, Reflection and summary
1. For the program itself, although it can accurately calculate the target coordinates, it can not automatically detect whether the player has entered the wrong error data (for example, positioning to two different fortresses), which can be optimized. The preliminary algorithm idea can consider calculating the triangle area of three intersection points, and report when it is greater than a certain threshold Wrong.
2. In the process of programming, the box numbers of UI are not in order, resulting in the corresponding error of input box in the code, which should be avoided in the future
3. In this program, the UI and the main program are written together. For large-scale projects, the UI and the main code need to be separated, so we should further learn the interface and connection methods.
Harvest:
1. Preliminary understanding of UI design with Pyqt5 and Qt designer
2. Reviewed the basic syntax of Python
3. I learned how to use Numpy