Preface

Since the last two blogs Python genetic and evolutionary algorithm toolbox and its application in constrained single objective function value optimization And genetic algorithm The shortest path of directed graph After that, I learned the official documents of the toolbox and the research of the source code, and I learned more about how to use genetic algorithm to solve more interesting problems.

Different from the previous paper, this paper uses the differential evolution algorithm to optimize the parameters C and Gamma in SVM. (it is also possible to use genetic algorithm, and the effect comparison will be given below)

Let's start with a brief review of the use of Python's high-performance utility genetic and evolutionary algorithm toolbox. For an optimization problem, it needs to do two steps to solve it: Step 1: define the problem class; step 2: write an execution script to call the Geatpy evolution algorithm template to solve the problem. In the previous blog, I introduced the specific usage in detail: https://blog.csdn.net/weixin_37790882/article/details/84034956 , but the complete Chinese course can refer to the official documents.

Let's start with the topic:

First, a brief description of the use of SVM. This paper uses Python's sklearn library to run SVM algorithm. The algorithm library of SVM in sklearn can be divided into two categories, one is classified algorithm library, including three categories: SVC, NuSVC and linearsvc. The other is regression algorithm library, including three classes: SVR, NuSVR and linearsvr. The related classes are wrapped in the sklearn.svm module.

text

This article focuses on using SVC class to iris data set The data are classified. The data format of iris data set is as follows:

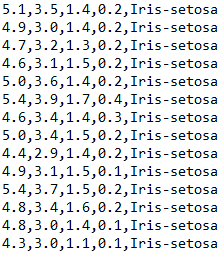
The first four columns are characteristic data and the fifth column is label data. There are three tags in the whole dataset: iris setosa, iris versicolor and iris virginica.

The general steps of data classification with SVC are as follows:

Step 1: read the feature data of training set, and save it in a "matrix" of Numpy array type, so that each column represents a feature, each row represents a group of data, and standardize the data.

Step 2: read the label data of the training set, and save it in a row vector of Numpy array type.

Step 3: find the optimal parameters C and Gamma.

Step 4: instantiate the object of SVC class with the optimal parameters (that is, create the classifier object), and call its member function fit() to fit the classifier model with the data of training set.

Step 5: read the feature data and label data of the test set in the same way as step 1 and step 2, and standardize the feature data.

Step 6: use the trained classifier in step 4 to predict the standardized feature data, and predict the corresponding labels of each group of feature data.

Step 7: compare the predicted tag data with the read test set tag data, and calculate the accuracy.

In the above steps, finding the optimal parameters C and Gamma is a key step. In general, the fixed step grid search strategy and cross validation are used to find the optimal parameters. In this paper, differential evolution algorithm is used to find the optimal parameter. The basic process of differential evolution algorithm is almost the same as that of general evolution algorithm. There is no need to elaborate here. Authoritative and easy to understand references are as follows:

Price, K.V., Storn, R.N. and Lampinen, J.A.. Differential Evolution:  A Practical Approach to Global Optimization. : Springer, 2005.

Code implementation (from Case 6 of single objective optimization in Geatpy website)

1) First, write the model to the user-defined problem class. The code is as follows:

# -*- coding: utf-8 -*-
"""MyProblem.py"""
import numpy as np
import geatpy as ea
from sklearn import svm
from sklearn import preprocessing
from sklearn.model_selection import cross_val_score
from multiprocessing.dummy import Pool as ThreadPool
class MyProblem(ea.Problem): # Inherit the Problem parent class
    def __init__(self):
        name = 'MyProblem' # Initialization name (function name, can be set at will)
        M = 1 # Initialize M (target dimension)
        maxormins = [-1] # Initialize maxormins (target minimax tag list, 1: minimize the target; - 1: maximize the target)
        Dim = 2 # Initialize Dim (decision variable dimension)
        varTypes = [0, 0] # Initialize varTypes (the type of the decision variable, element 0 means the corresponding variable is continuous; 1 means discrete)
        lb = [2**(-8)] * Dim # Lower bound of decision variables
        ub = [2**8] * Dim # Upper bound of decision variables
        lbin = [1] * Dim # Lower boundary of decision variable (0 means lower boundary without the variable, 1 means included)
        ubin = [1] * Dim # Upper boundary of decision variable (0 for upper boundary without the variable, 1 for inclusion)
        # Calling the parent class construction method to complete the instantiation
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)
        # Some data used in the calculation of objective function
        fp = open('iris_train.data')
        datas = []
        data_targets = []
        for line in fp.readlines():
            line_data = line.strip('\n').split(',')
            data = []
            for i in line_data[0:4]:
                data.append(float(i))
            datas.append(data)
            data_targets.append(line_data[4])
        fp.close()
        self.data = preprocessing.scale(np.array(datas)) # Characteristic data of training set (normalization)
        self.dataTarget = np.array(data_targets)
    
    def aimFunc(self, pop): # Objective function, using multithreading to accelerate calculation
        Vars = pop.Phen # Get decision variable matrix
        pop.ObjV = np.zeros((pop.sizes, 1)) # Initializing individual objective function value column vector of population
        def subAimFunc(i):
            C = Vars[i, 0]
            G = Vars[i, 1]
            svc = svm.SVC(C=C, kernel='rbf', gamma=G).fit(self.data, self.dataTarget) # Creating classifier object and fitting classifier model with training set data
            scores = cross_val_score(svc, self.data, self.dataTarget, cv=10) # Calculate the score of cross validation
            pop.ObjV[i] = scores.mean() # Take the average score of cross validation as the objective function value
        pool = ThreadPool(2) # Set the size of the pool
        pool.map(subAimFunc, list(range(pop.sizes)))
    
    def test(self, C, G): # Test the test set with the optimized C and Gamma
        # Read test set data
        fp = open('iris_test.data')
        datas = []
        data_targets = []
        for line in fp.readlines():
            line_data = line.strip('\n').split(',')
            data = []
            for i in line_data[0:4]:
                data.append(float(i))
            datas.append(data)
            data_targets.append(line_data[4])
        fp.close()
        data_test = preprocessing.scale(np.array(datas)) # Characteristic data of test set (normalization)
        dataTarget_test = np.array(data_targets) # Label data for test set
        svc = svm.SVC(C=C, kernel='rbf', gamma=G).fit(self.data, self.dataTarget) # Creating classifier object and fitting classifier model with training set data
        dataTarget_predict = svc.predict(data_test) # Using the trained classifier object to predict the test set data
        print("Test set data classification accuracy = %s%%"%(len(np.where(dataTarget_predict == dataTarget_test)[0]) / len(dataTarget_test) * 100))

In the above code, the average score obtained from cross validation is used as the objective function value to be optimized. Because the higher the score is, the better the parameter is. Therefore, the maxormins above is set to [- 1], indicating that the objective to be optimized is a maximized objective. Set the search interval of C and Gamma to the negative 8th power of 2 to the 8th power of 2.

2) Then create the execution script, call the differential evolution algorithm template SOEA, and use the differential evolution algorithm optimization of DE/rand/1/bin to optimize the above defined model to be optimized. The code is as follows:

# -*- coding: utf-8 -*-
"""main.py"""
import numpy as np
import geatpy as ea # import geatpy
from MyProblem import MyProblem # Import custom question interface
if __name__ == '__main__':
    """===============================Instantiate problem object==========================="""
    problem = MyProblem() # Generate problem object
    """=================================Population settings==============================="""
    Encoding = 'RI'       # Coding mode
    NIND = 20             # Population size
    Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders) # Create area descriptor
    population = ea.Population(Encoding, Field, NIND) # Instantiate the population object (at this time, the population has not been initialized, just to complete the instantiation of the population object)
    """===============================Algorithm parameter setting============================="""
    myAlgorithm = ea.soea_DE_rand_1_bin_templet(problem, population) # Instantiate an algorithm template object
    myAlgorithm.MAXGEN = 30 # Maximum evolution algebra
    myAlgorithm.trappedValue = 1e-6 # Judgment threshold of "evolutionary stagnation"
    myAlgorithm.maxTrappedCount = 10 # The maximum upper limit of evolution stagnation counter. If the successive maxTrappedCount generations are judged to be stalled, the evolution will be terminated
    """==========================Calling algorithm template for population evolution======================="""
    [population, obj_trace, var_trace] = myAlgorithm.run() # Execute algorithm template
    population.save() # Save the information of the last generation population to a file
    # Output result
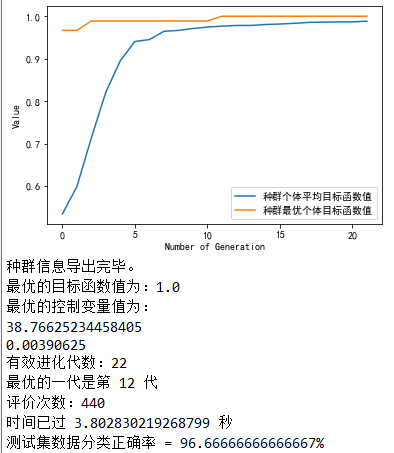
    best_gen = np.argmin(problem.maxormins * obj_trace[:, 1]) # Record the generation of the best species group
    best_ObjV = obj_trace[best_gen, 1]
    print('The optimal objective function value is:%s'%(best_ObjV))
    print('The optimal control variables are:')
    for i in range(var_trace.shape[1]):
        print(var_trace[best_gen, i])
    print('Effective evolution algebra:%s'%(obj_trace.shape[0]))
    print('The best generation is the %s generation'%(best_gen + 1))
    print('Evaluation times:%s'%(myAlgorithm.evalsNum))
    print('Time has passed. %s second'%(myAlgorithm.passTime))
    """=================================Test result==============================="""
    problem.test(C = var_trace[best_gen, 0], G = var_trace[best_gen, 1])

The operation results are as follows:

Epilogue

The above execution script calls DE/rand/1/bin differential evolution algorithm for evolutionary optimization. In fact, it can call other algorithm templates such as genetic algorithm and genetic strategy for evolutionary optimization. For example, call the most classical genetic algorithm:

# Replace this line with the one in main.py above
myAlgorithm = ea.soea_SGA_templet(problem, population)

Modify the main.py code as described in the note above, and the result is as follows:

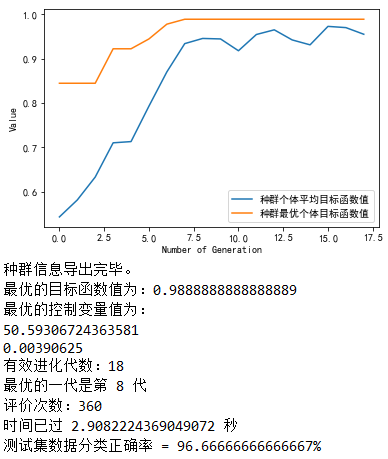
It can be seen that the effect of parameter optimization with SGA is slightly less than that with DE/rand/1/bin differential evolution algorithm, which means that for the data of training set, the accuracy of the latter classification is lower than the former; but for the test set, the accuracy of the two classification is the same.

Finally, I will review the "evolution algorithm routine" mentioned in the previous blog (the previous one is about "heredity", which is extended to "evolution"):

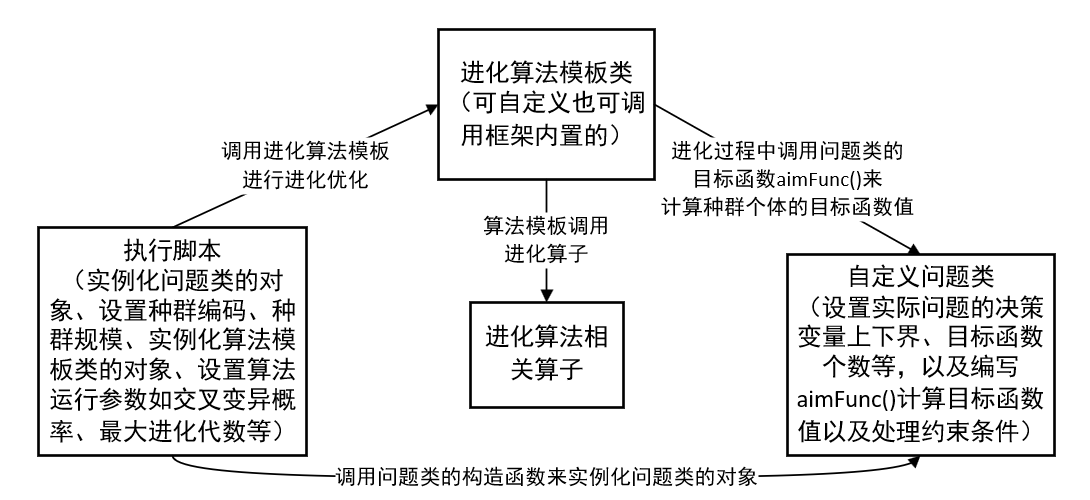
This scheme realizes the decoupling between the specific problem, the algorithm used and the related operators called. However, many template classes and related operators of evolutionary algorithm have been built into the Geatpy toolbox, which can be called directly. For the solution of practical problems, we only need to care how to write the problem in the custom problem class.

The experimental code used in this paper well reflects this process. In the whole process, I don't care about the specific implementation of evolutionary algorithm, just how to write the model to be optimized in the custom problem class MyProblem.

More detailed tutorials can be found in: http://geatpy.com/index.php/geatpy%E6%95%99%E7%A8%8B/

I will continue to learn and explore more in-depth usage of the toolkit later. I hope this article can help you to record your learning and help you!