I. Preface
At the beginning of writing the third person control, we used WASD to control the role in the computer test
Later, it needed to be released to the mobile phone, so a rocker was added
The code of keyboard control role has been written. The role moves in eight directions
2, Traditional control ideas
//When the rocker is moving, the character begins to run void OnJoystickMove(MovingJoystick move) { if (move.joystickName != "EasyJoystick") { return; } //Get rocker offset float joyPositionX = move.joystickAxis.x; float joyPositionY = move.joystickAxis.y; if (joyPositionY != 0 || joyPositionX != 0) { //Set the orientation of the character (towards the current coordinate + rocker offset) transform.LookAt(new Vector3(transform.position.x + joyPositionX, transform.position.y, transform.position.z + joyPositionY)); //Move player's position (move towards position) transform.Translate(Vector3.forward * Time.deltaTime * 7.5F); //Play running animation animation.CrossFade("Run"); } }
3, Control rocker angle
If I want to control the role according to the traditional idea of the rocker, it is very troublesome to rewrite the control role code, so I will determine the current direction of the rocker by calculating the rotation angle of the rocker
ok, now let's start typing
First, let's debug and observe the return values of x-axis and y-axis of the rocker
//Moving the rocker
void OnJoystickMove(MovingJoystick move) { Debug.Log(move.joystickAxis.x + "," + move.joystickAxis.y); }
The debugging results are as follows:
Left: x = -1, y = 0; clockwise rotation X gradually increases, Y gradually increases
Up: x = 0, y = 1; clockwise rotation X gradually increases, Y gradually decreases
Right: x = 1, y = 0; clockwise rotation X decreases gradually, Y decreases gradually
Lower: x = 0, y = -1; clockwise rotation X gradually decreases, Y gradually increases
We see the bottom of the rocker as two semicircles, the upper semicircle and the lower semicircle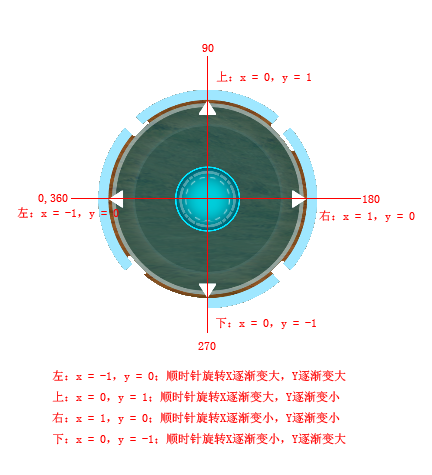
Then:
When the X-axis moves to the left, X = -1; when the X-axis moves to the right, X = 1; when the X-axis rotates 180 degrees from left to right
When Y-axis moves to the left, Y = 0; when Y-axis moves to the right, Y = 0; Y-axis rotates 180 degrees from left to right
If you look directly at my debugging results, you must be a little dizzy. It is recommended to refer to my debugging results while debugging, so that you can understand
What if we want to calculate the degree of rotation of the current rocker in the upper left corner?
People who have studied in primary school can do it, only to see that the heads of - 1 and 0 returned from the rocker are confused, so do I. It took me a long time to finish it
When the rocker is moved to the left, it is 0 degree, 360 degree (because 360 degree is a circle, it has been around the far point)
90 degrees when the rocker moves up
180 degrees when the rocker moves to the right
270 degrees when the rocker moves down
Now that you know how many degrees, it's much easier
The formula is as follows:
When the X axis is on the right, it is 1, i.e. the X axis is 180 degrees, then: 1 * 90 + 90 = 180
Current X-axis rotation angle is: X-axis return value * 90 degrees + 90 degrees
Do you think it's over? It's too early to be happy. Only the rotation angle of the upper half circle can be calculated by this formula
Now we want to get the rotation angle of the lower semicircle, and then use the rotation angle of the upper semicircle + the rotation angle of the lower semicircle = the current rotation angle
How do we calculate the rotation angle when the rocker moves to the bottom half circle?
We already know that the Y-axis is 0 on the left, 0 on the right, and - 1 on the bottom. Continue to use the formula to calculate the X-axis
Y left: 0 * 90 + 90 = 90
On Y: 1 * 90 + 90 = 180
Under Y: - 1 * 90 + 90 = 0
Y right: 0 * 90 + 90 = 90
X left: - 1 * 90 + 90 = 0
On X: 0 * 90 + 90 = 90
Under X: 0 * 90 + 90 = 90
X right: 1 * 90 + 90 = 180
It can be concluded from the calculation results
When the Y axis is less than 90 degrees, the rocker is in the lower semicircle
When Y-axis is less than 90 degrees and X is less than 90 degrees, it is lower left: 270 degrees + Y-axis rotation angle
When Y-axis is less than 90 degrees and X is more than 90 degrees, it is lower right: 180 degrees + Y-axis rotation angle
Now that I've got the idea, I'll start typing the code. There are not many codes. I've posted them directly. After reading the appeal text, I'm sure you already know what's going on with these codes
///Calculate rocker angle < summary > ///Calculate rocker angle /// </summary> ///< param name = "joypositionx" > rocker X axis < / param > ///< param name = "joyposition Y" > rocker Y axis < / param > ///< returns > returns how many degrees the current rocker rotates < / returns > private float CalculaAngle(float _joyPositionX, float _joyPositionY) { float currentAngleX = _joyPositionX * 90f + 90f;//Current angle of X axis float currentAngleY = _joyPositionY * 90f + 90f;//Current angle of Y axis //Lower half circle if (currentAngleY < 90f) { if (currentAngleX < 90f) { return 270f + currentAngleY; } else if (currentAngleX > 90f) { return 180f + (90f - currentAngleY); } } return currentAngleX; }
ok, now that we know how many degrees the current rocker has rotated, we can easily use the angle to determine the current direction of movement
When using keyboard control:
A = left
WA = upper left
W = upper
WD = right upper
D = right
SD = right lower
S = lower
SA = left lower
When the rocker angle is 0 degrees, turn left
When the rocker angle is 90 degrees, go up
When the rocker angle is 180 degrees, go right
Then we can't write like this. Can you be sure that players operate the rocker so precisely?
Because my control role here is eight directions, so: 360 / 8 = 45
There are 45 degrees to trigger in each direction, so the following solutions are obtained:
Top: current angle < = 90 + 45 / 2 = 112.5 & & current angle > = 90 - 45 / 2 = 67.5
The following codes are obtained as follows:
float currentAngle = CalculaAngle(joyPositionX, joyPositionY); if (currentAngle <= 22.5f && currentAngle >= 0f || currentAngle <= 360f && currentAngle >= 337.5f)//0; left CurrentDire = "A"; else if (currentAngle <= 67.5f && currentAngle >= 22.5f)//45; left upper CurrentDire = "WA"; else if (currentAngle <= 112.5f && currentAngle >= 67.5f)//90; on CurrentDire = "W"; else if (currentAngle <= 157.5f && currentAngle >= 112.5f)//135; right upper. CurrentDire = "WD"; else if (currentAngle <= 202.5f && currentAngle >= 157.5f)//180; right. CurrentDire = "D"; else if (currentAngle <= 247.5f && currentAngle >= 202.5f)//225; right bottom. CurrentDire = "SD"; else if (currentAngle <= 292.5f && currentAngle >= 247.5f)//270 below CurrentDire = "S"; else if (currentAngle <= 337.5f && currentAngle >= 292.5f)//315; left lower CurrentDire = "SA";
It's a success. Let's run on the mobile phone. This is the eight direction operation effect of the rocker I want

