Although binary search tree can improve the efficiency of search, but there is a defect, that is, when the parameters of the tree are in order or close to order, it will degenerate into a single tree, and the search efficiency will become o(n)
Therefore, a method to solve the above problem is invented: when a new node is inserted into a binary search tree, if the absolute value of the height difference between the left and right subtrees of each node is not more than 1 (the nodes in the tree need to be adjusted), the height of the tree can be reduced, thus reducing the average search length.
In order to commemorate the inventor of this solution, it is called AVL tree
An AVL tree is either an empty tree or a binary search tree with the following properties:
The premise of an AVL tree is that the AVL tree must be a binary search tree, and the binary search tree may not be an AVL tree
- Its left and right subtrees are AVL trees
- The absolute value of the difference between the height of left and right subtrees (balance factor for short) shall not exceed 1 (- 1 / 0 / 1)
First, how to judge the balance factor of a tree?
I choose the height of the right subtracted from the height of the left subtracted.
//Because the balance factor of AVL tree itself has only three possibilities: 0, - 1, 1 //Before inserting a new node //0 ----- pParent is the leaf node = =============, the inserted node may be inserted into the left subtree and the right subtree, so the parent node may become + - 1 after insertion //1 ----- pParent only has right child = ========, inserted node can only insert left subtree -] 0 //-1 ----- pParent only has left child = =========, inserted node can only insert right subtree -] 0 //It means that in the last two cases, it only affects the balance factor of parents, but not the balance factor of parents' upward node
When the balance factor is 1 / - 1 before insertion, it becomes 0 after insertion
Then, the equilibrium factor is 0 before insertion: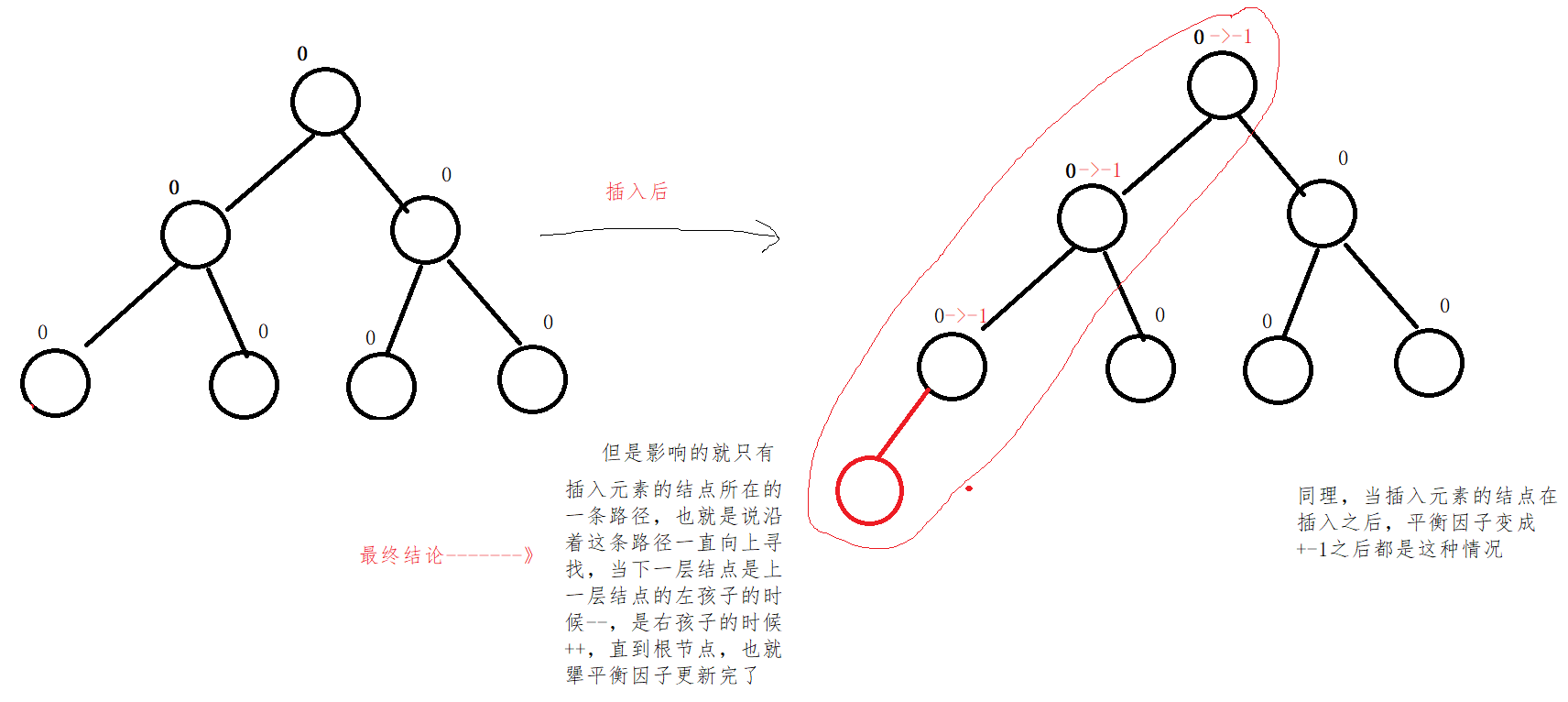
First of all, it introduces what is left single selection and what is right single rotation.
Left and right turns of trees
Right single rotation scene:
Right single rotation: the newly inserted node is inserted to the left (outside) of the higher subtree (the higher subtree is the left subtree)
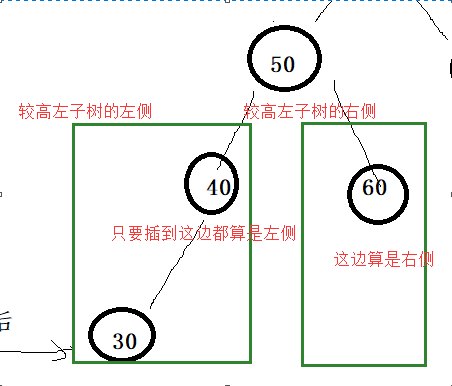

There are three special nodes in the process of rotation:
Three special nodes, one of which may be empty
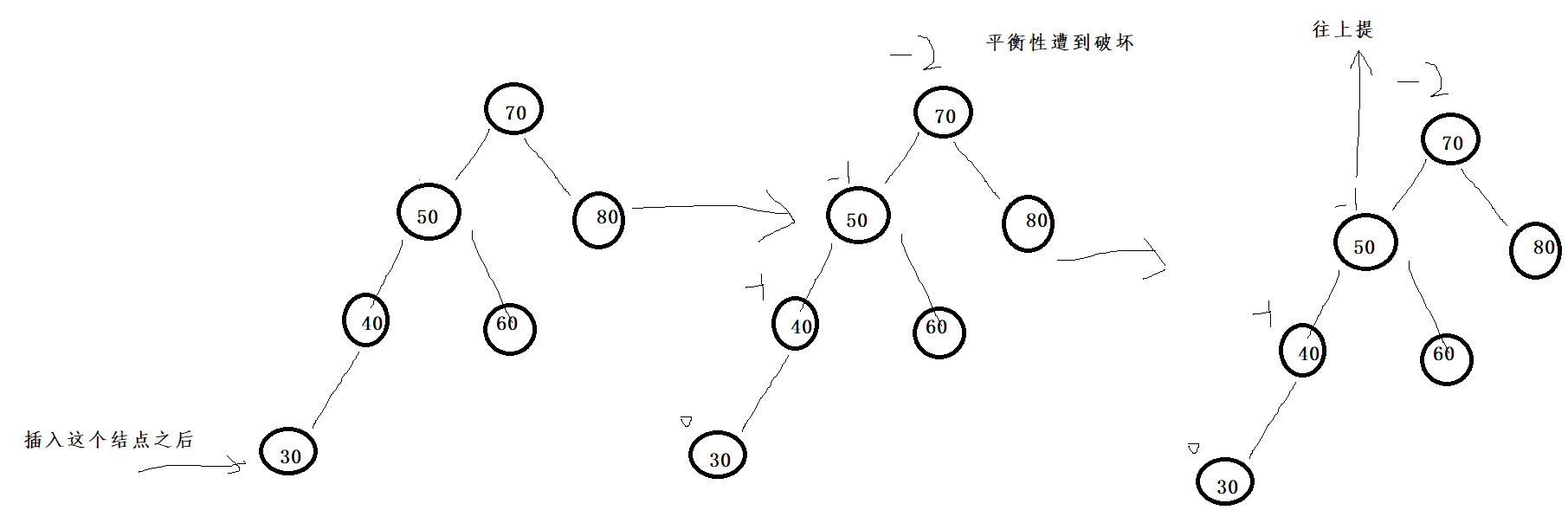
If you mention the root of the higher subtree, that is to say, which node is unbalanced, you should mention the higher one of its left and right children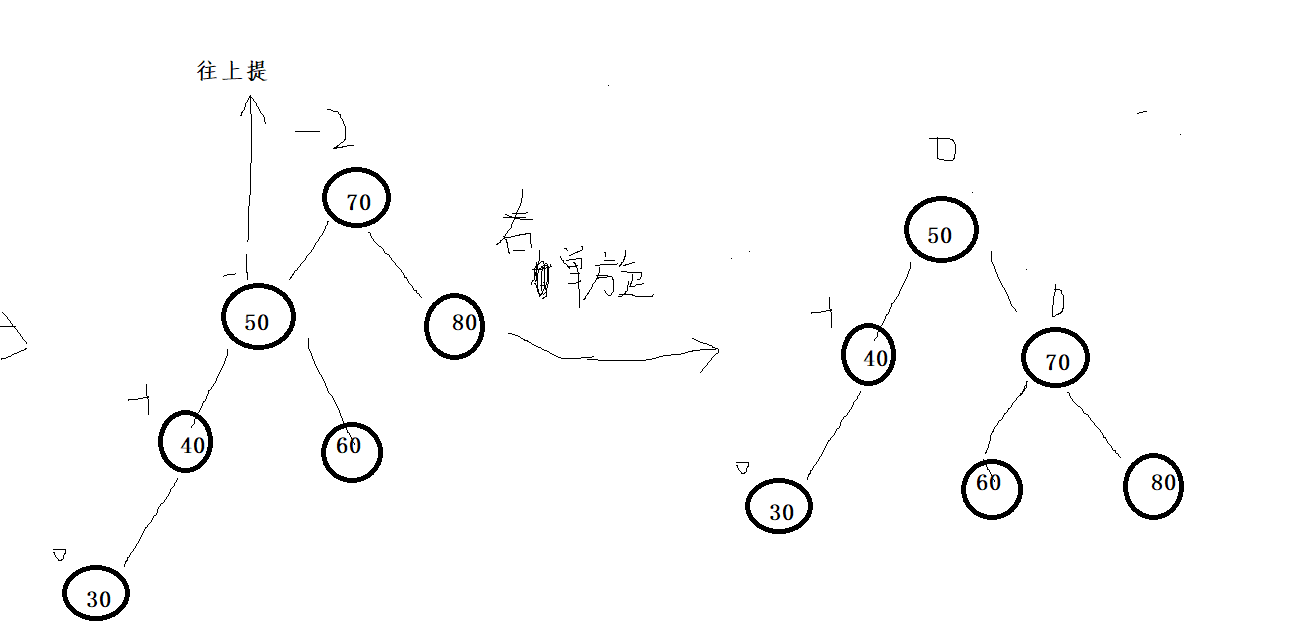
In the other case, right single rotation: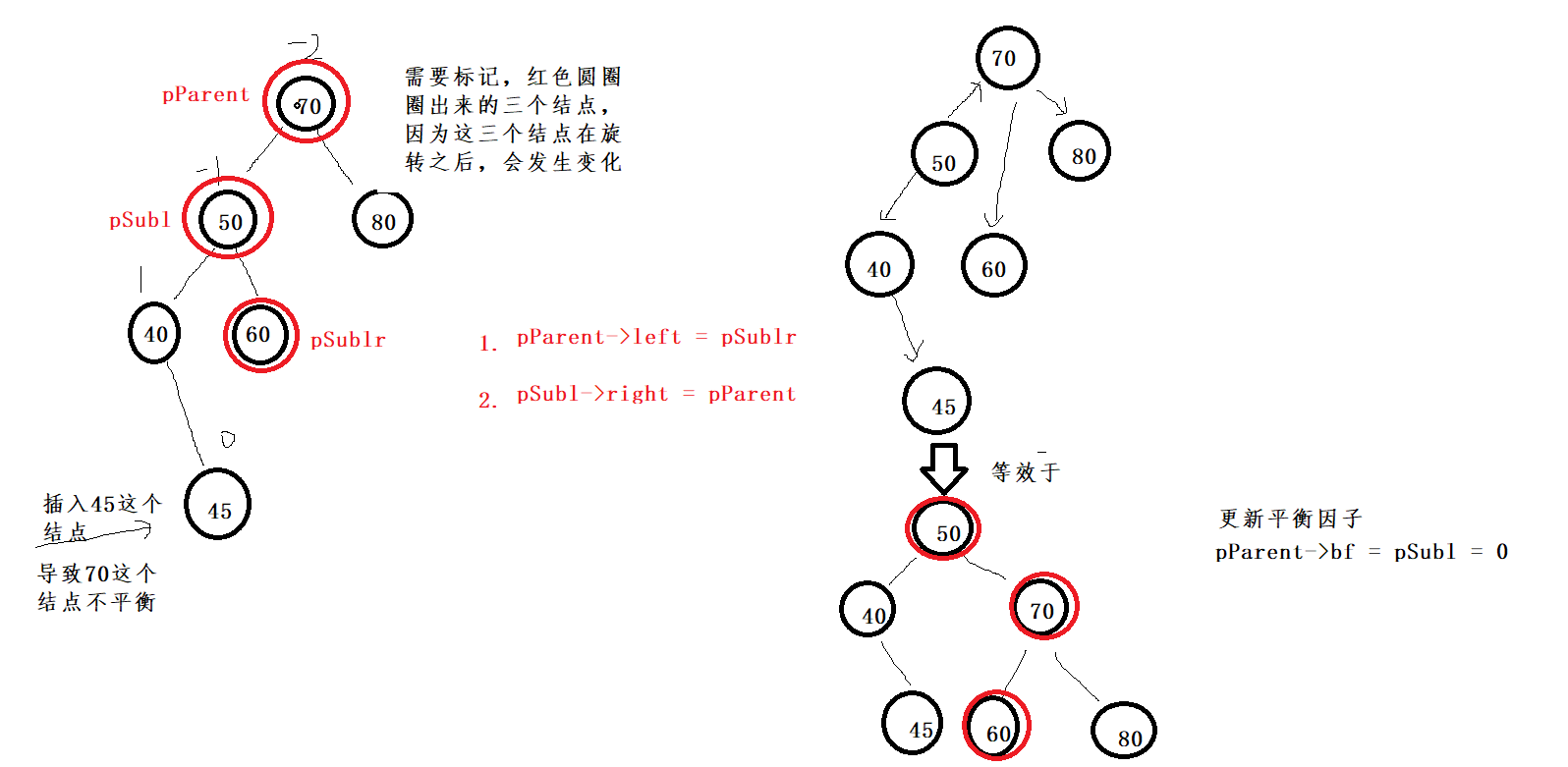
Third right single rotation: (left single branch)
But even if this node is empty, it doesn't affect anything. It just needs to list one by one the three situations of right single rotation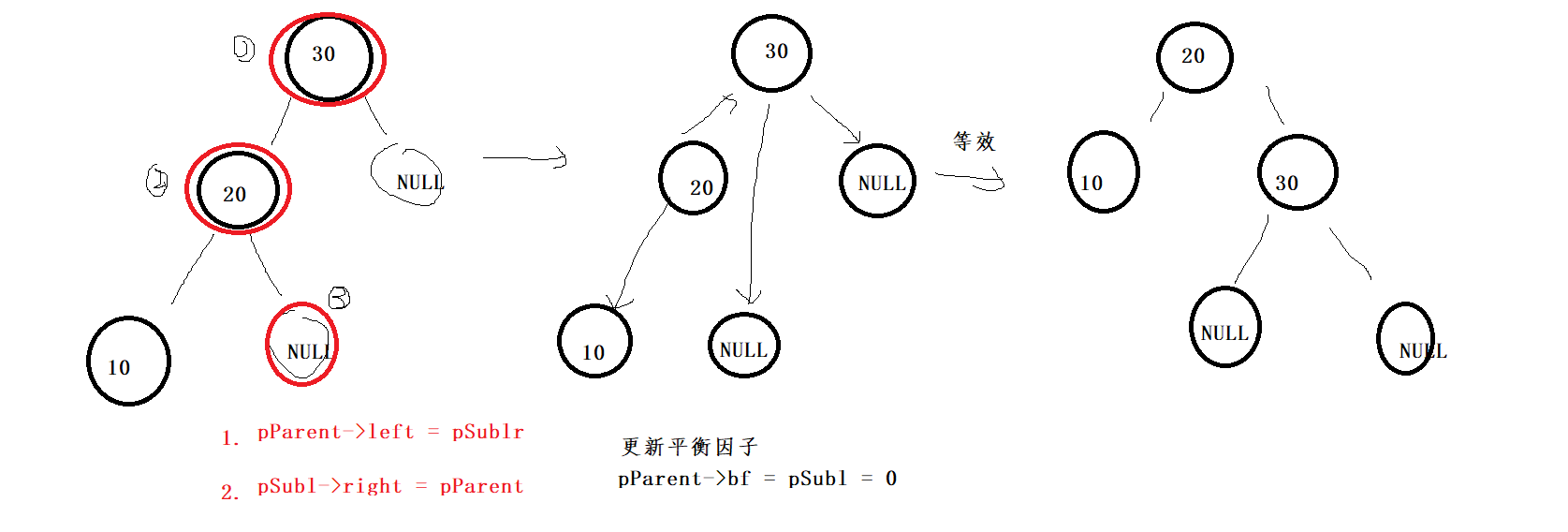
The above three scenes are the three scenes of right single rotation
Although the scenarios are different, the code given in each scenario is indeed the same. The three scenarios are given just to make people see them more clearly
Of course, you need to update the parent pointer fields of three special nodes after you finish the above operations

In summary, there are three steps 1. Change the left and right child pointer fields of special nodes 2. Update the balance factor of special nodes 3. Update the pointer domain of the parent node of the special node 4. Judge whether the highest vertex is the root node, then complete the connection and update the balance factor
To facilitate annotation, mark from top to bottom:
pParent: special node 1
pSubl: special node 2
pSublr: special node 3

Right single rotation code:
//Right single rotation code void RotateRight(Node* pParent_1) //Special node 1 { Node* pSubL = pParent_1->_pLeft; //Special node 2 Node* pSubLR = pSubL->_pRight; //Special node 3 pParent->_pLeft = pSubLR; //The main purpose of void determination here is to avoid the third case, left single branch if (pSubLR) //If special node 3 is not empty, let the parent pointer field of special node 3 point to special node 1 pSubLR->_pParent = pParent_1; pSubL->_pRight = pParent_1; //Next, we deal with the pparent ﹣ 1 node in the special node //We don't know whether it is a root node or not, because the part of pParent we draw is a root node, but we can't guarantee that there are no other nodes above //So we need to discuss it according to the situation //If pParent_1 is a subtree, there are trees on the top of pParent //In order to prevent the loss of the parents node of pParent_1, we first save the parents of pParent Node* pPParent = pParent_1->_pParent; //The parent node of special node 1 may be empty pParent_1->_pParent = pSubL; //Reset parents pSubL->_pParent = pPParent; if (pPParent == nullptr) //It indicates that special node 1 has no parents, { _pRoot = pSubL; //Without parents, the root node in the class is directly updated to special node 2 } else //Note that special node 1 has parents { if (pPParent->_pLeft == pParent_1) //At this time, although the parents of special node 1 are updated, the original parents of special node 1 still regard special node 1 as their own child //So if special node 1 is the left child of the previous parents, you need to make his left child point to special node 2 now, and vice versa pPParent->_pLeft = pSubL; else pPParent->_pRight = pSubL; } //And then there's the update balance factor //After the option is updated, the balance factors of special node 1 and special node 2 become 0 //The equilibrium factor of parents of special node 1 is invariant pParent_1->_bf = pSubL->_bf = 0; }
Left single rotation code:
Select one from the left radio: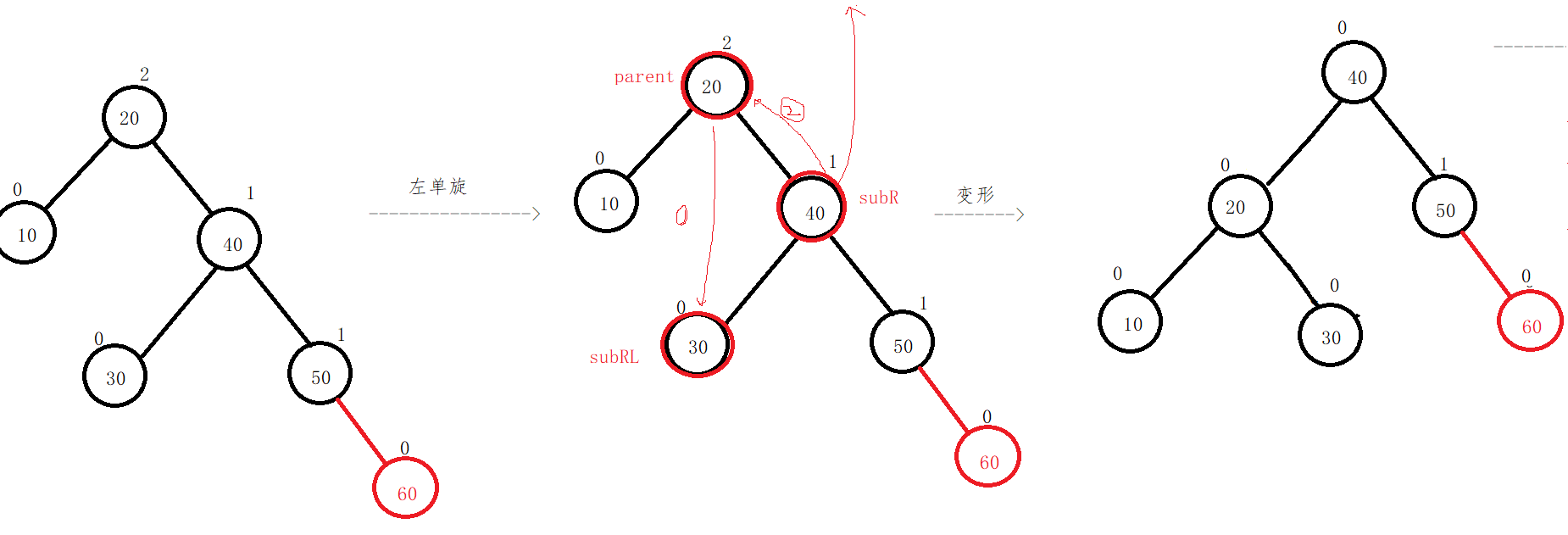
According to the right single rotation, the left single rotation can be written:
//Left spin void RotateLeft(Node* pParent_1) //Special node 1 { Node* pSubR = pParent_1->_pRight; //Special node 2 Node* pSubRL = pSubR->_pLeft; //Special node 3 pParent_1->_pRight = pSubRL; if (pSubRL) pSubRL->_pParent = pParent_1; pSubR->_pLeft = pParent_1; Node* pPParent = pParent_1->_pParent; pSubR->_pParent = pPParent; pParent_1->_pParent = pSubR; if (pPParent == nullptr) { _proot = pSubR; } else { if (pParent_1 == pPParent->_pLeft) { pPParent->_pLeft = pSubR; } else { pPParent->_pRight = pSubR; } } pParent_1->_bf = pSubR->_bf = 0; }
Left single rotation right single rotation:
In one case:
First, the left subtree of the unbalanced node is rotated to the left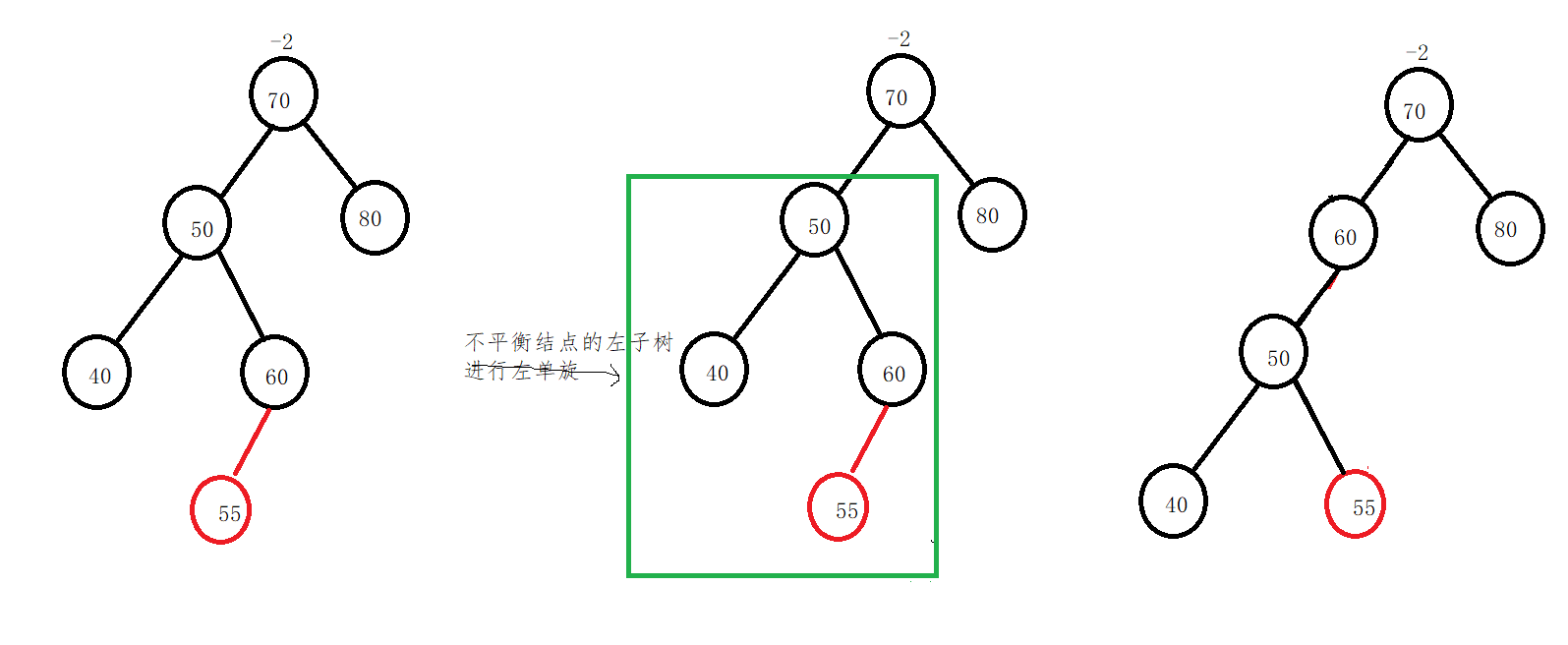
Right single rotation of the whole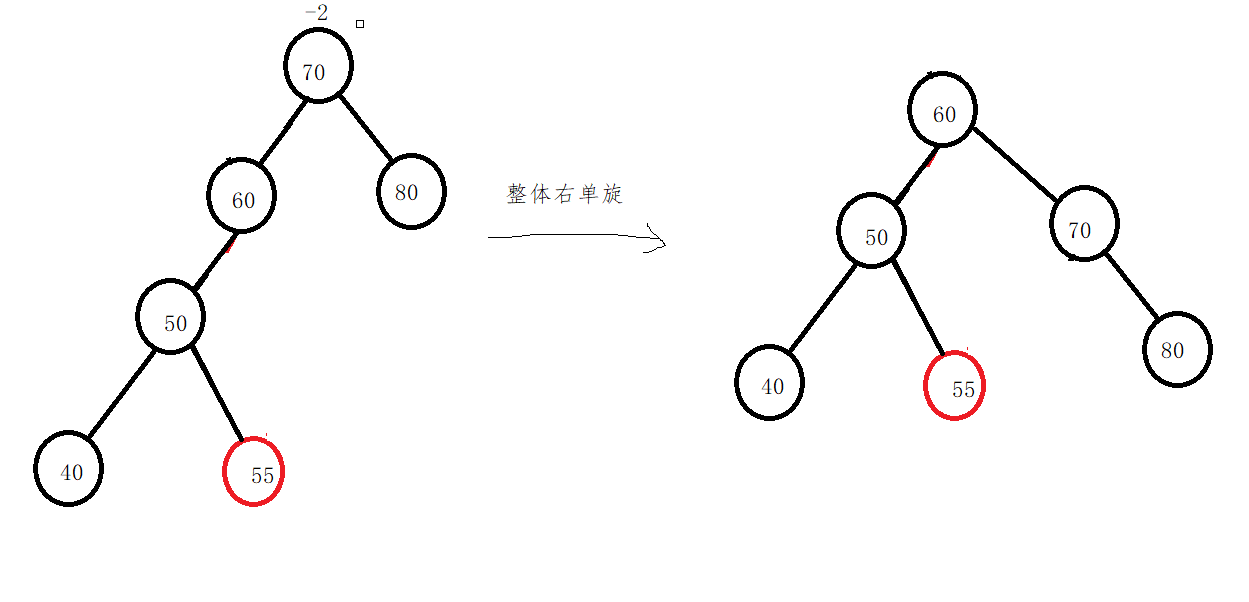
Left single rotation right single rotation code:
This is not only the reuse of left single rotation and right single rotation, because there are some special cases. When left single rotation and right single rotation, we directly make the balance factor of special node 1 and special node 2 equal to 0 at the end, but there are some specific methods for some specific AVL trees when rotating, so we need to judge some cases.
//Left single turn right single turn void RotateLR(Node* pParent) { //Save node before rotation Node* pSubR = pParent->_pLeft; Node* pSubRL = pSubR->_pRight; int bf = pSubRL->_bf; RotateLeft(pParent->_pLeft); RotateRight(pParent); //Three situations //BF = = 1 | - 1 | - 0,0 has been dealt with internally if (bf == 1) pSubRL->_bf = -1; else if (bf == -1) pParent->_bf = 1; }
Right single rotation left single rotation:
The same is true for right single spin and left single spin
Right single rotation left single rotation code:
//Right single spin left single spin void RotateRL(Node* pParent) { //It is found that the equilibrium factors of some nodes need to be updated during the right left double rotation, which is also a special case //Here, we will not draw a picture for analysis, but directly give the code Node* pSubR = pParent->_pRight; Node* pSubRL = pSubR->_pLeft; int bf = pSubRL->_bf; RotateRight(pParent->_pRight); RotateLeft(pParent); //Three situations //BF = = 1 | - 1 | - 0,0 has been dealt with internally if (bf == 1) pParent->_bf = -1; else if (bf == -1) pSubR->_bf = 1; }
Final code:
#include<iostream> using namespace std; template<class T> //Node structure struct AVLTreeNode { AVLTreeNode(const T& data) : _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr) , _data(data), _bf(0) {} AVLTreeNode<T>* _pLeft; // The left child of this node AVLTreeNode<T>* _pRight; // The right child of this node AVLTreeNode<T>* _pParent; // Parents of the node T _data; int _bf; // Balance factor of this node }; //In the following insert operation, to determine the balance factor of a node, we default to use the right subtree - the left subtree //Again, the default is right subtree - left subtree template<class T> class AVLTree { typedef AVLTreeNode<T> Node; public: AVLTree() :_pRoot(nullptr) {} bool Insert(const T& data) { //AVL tree may be empty if (nullptr == _pRoot) { _pRoot = new Node(data); return true; } //Not empty //First, insert the binary search tree //The first thing to say is that the insertion position is absolutely that the leaf node has only the left child's node and the right child's node //It will never be inserted at nodes with both left and right children Node* pCur = _pRoot; Node* pParent = nullptr; while (pCur) { pParent = pCur; //Save the parent node of the node to be inserted if (data < pCur->_data) pCur = pCur->_pLeft; else if (data > pCur->_data) pCur = pCur->_pRight; else return false; //This means that if the value tree to be inserted already exists, it will be returned directly. The values inserted in the default tree are different } //Insert new node pCur = new Node(data); //Create node first if (data > pParent->_data) pParent->_pRight = pCur; else pParent->_pLeft = pCur; pCur->_pParent = pParent; //Finally, let the parents of the new node point to pParent //Every time a new node is inserted, the balance factor of the parent node must change //Renew the balance factor of parents while (pParent) //Circular condition is that parents are not empty { if (pCur == pParent->_pLeft) //If it is a left subtree, then the balance factor of parents --. Because my default balance factor algorithm is to subtract the left subtree from the right subtree pParent->_bf--; else pParent->_bf++; //Because the balance factor of AVL tree itself has only three possibilities: 0, - 1, 1 //Before inserting a new node //0 ----- pParent is the leaf node = =============, the inserted node may be inserted into the left subtree and the right subtree, so the parent node may become + - 1 after insertion //1 ----- pParent only has right child = ========, inserted node can only insert left subtree -] 0 //-1 ----- pParent only has left child = =========, inserted node can only insert right subtree -] 0 //It means that in the last two cases, it only affects the balance factor of parents, but not the balance factor of parents' upward node if (pParent->_bf == 0) //That is to say, after the above + + || -- is finished, the balance factor of the inserted element's node becomes 0, which is the last two situations I mentioned above. Because it does not affect the other nodes, it can be returned directly return true; else if (pParent->_bf == -1 || pParent->_bf == 1) //This is the case of the parent node that will affect the insertion node, and then all the nodes up { //Adjust the position of pCur here pCur = pParent; //At this point, you need to enter the while loop to update the + + | -- at the beginning pParent = pCur->_pParent; } else { //Balance factor of parent = = 2 | - 2 //It means that the nature of AVL tree has been violated at this time -- at this time, the tree is unbalanced, and the tree with pParent as root should be rotated //There are four kinds of rotation //Left spin //Right single rotation //If the equilibrium factor is + 2, because we take the left subtree from the right subtree, so this is the left single rotation, otherwise it is the right single rotation //Of course, it is not enough to judge only the unbalanced nodes, because there are left-right double rotation and right-left double rotation, so it is necessary to judge the left and right subtrees of the unbalanced nodes //Left and right double rotation: left radio, right single rotation //Right left double rotation: left radio, right single rotation if (pParent->_bf == 2) { //The right subtree height of pParent //The equilibrium factor of pCur is + 1 //Since only one path of the inserted node will be modified after insertion, pCur is the child node of pParent, so you don't need to know whether it is the left or right child, because you don't need to know if (pCur->_bf == 1) { //Left spin RotateLeft(pParent); } else { //The equilibrium factor of pCur is - 1 //Right left double spin RotateRL(pParent); } } else { //Left subtree height of pParent //pParent->_bf == -2 if (pCur->_bf == -1) { //Right single rotation RotateRight(pParent); } else { //Left and right rotation RotateLR(pParent); } } break; //When the rotation is completed, you don't need to enter the while again. You can exit directly because the number of layers before and after the imbalance caused by the insertion of nodes does not change, which has no impact on the above } } return true; } //In order to avoid confusion with the pParent in the node structure, I use pParent_1 instead of the special node 1 void RotateRight(Node* pParent_1) //Special node 1 { Node* pSubL = pParent_1->_pLeft; //Special node 2 Node* pSubLR = pSubL->_pRight; //Special node 3 pParent_1->_pLeft = pSubLR; //The main purpose of void determination here is to avoid the third case, left single branch if (pSubLR) //If special node 3 is not empty, let the parent pointer field of special node 3 point to special node 1 pSubLR->_pParent = pParent_1; pSubL->_pRight = pParent_1; //Next, we deal with the pparent ﹣ 1 node in the special node //We don't know whether it is a root node or not, because the part of pParent we draw is a root node, but we can't guarantee that there are no other nodes above //So we need to discuss it according to the situation //If pParent_1 is a subtree, there are trees on the top of pParent //In order to prevent the loss of the parents node of pParent_1, we first save the parents of pParent Node* pPParent = pParent_1->_pParent; //The parent node of special node 1 may be empty pParent_1->_pParent = pSubL; //Reset parents pSubL->_pParent = pPParent; if (pPParent == nullptr) //It indicates that special node 1 has no parents, { _pRoot = pSubL; //Without parents, the root node in the class is directly updated to special node 2 } else //Note that special node 1 has parents { if (pPParent->_pLeft == pParent_1) //At this time, although the parents of special node 1 are updated, the original parents of special node 1 still regard special node 1 as their own child //So if special node 1 is the left child of the previous parents, you need to make his left child point to special node 2 now, and vice versa pPParent->_pLeft = pSubL; else pPParent->_pRight = pSubL; } //And then there's the update balance factor //After the option is updated, the balance factors of special node 1 and special node 2 become 0 //The equilibrium factor of parents of special node 1 is invariant pParent_1->_bf = pSubL->_bf = 0; } //Left spin void RotateLeft(Node* pParent_1) //Special node 1 { Node* pSubR = pParent_1->_pRight; //Special node 2 Node* pSubRL = pSubR->_pLeft; //Special node 3 pParent_1->_pRight = pSubRL; if (pSubRL) pSubRL->_pParent = pParent_1; pSubR->_pLeft = pParent_1; Node* pPParent = pParent_1->_pParent; pSubR->_pParent = pPParent; pParent_1->_pParent = pSubR; if (pPParent == nullptr) { _pRoot = pSubR; } else { if (pParent_1 == pPParent->_pLeft) { pPParent->_pLeft = pSubR; } else { pPParent->_pRight = pSubR; } } pParent_1->_bf = pSubR->_bf = 0; } //Right single spin left single spin void RotateRL(Node* pParent) { //It is found that the equilibrium factors of some nodes need to be updated during the right left double rotation, which is also a special case //Here, we will not draw a picture for analysis, but directly give the code Node* pSubR = pParent->_pRight; Node* pSubRL = pSubR->_pLeft; int bf = pSubRL->_bf; RotateRight(pParent->_pRight); RotateLeft(pParent); //Three situations //BF = = 1 | - 1 | - 0,0 has been dealt with internally if (bf == 1) pParent->_bf = -1; else if (bf == -1) pSubR->_bf = 1; } //Left single turn right single turn void RotateLR(Node* pParent) { Node* pSubR = pParent->_pLeft; Node* pSubRL = pSubR->_pRight; int bf = pSubRL->_bf; RotateLeft(pParent->_pLeft); RotateRight(pParent); //Three situations //BF = = 1 | - 1 | - 0,0 has been dealt with internally if (bf == 1) pSubRL->_bf = -1; else if (bf == -1) pParent->_bf = 1; } void InOreder() //Sequential traversal { _InOrder(_pRoot); } bool Tree_Hight() //Judge whether this tree is an AVL tree { return _Tree_Hight(_pRoot); } private: void _InOrder(Node* pRoot) //Sequential traversal { if (pRoot == nullptr) return; _InOrder(pRoot->_pLeft); cout << pRoot->_data << endl; _InOrder(pRoot->_pRight); } bool _Tree_Hight(Node* pRoot) //Judge whether AVL tree { if (pRoot == nullptr) return true; int Left_Hight = Hight(pRoot->_pLeft); int Right_Hight = Hight(pRoot->_pRight); int bf = Right_Hight - Left_Hight; //Self calculated balance factor if (abs(bf) > 1 || bf != pRoot->_bf) return false; return _Tree_Hight(pRoot->_pLeft) && _Tree_Hight(pRoot->_pRight); } int Hight(Node* pRoot) { if (pRoot == nullptr) return 0; int L = Hight(pRoot->_pLeft); int R = Hight(pRoot->_pRight); return L > R ? L + 1 : R + 1; } Node* _pRoot; }; void test() { int array[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 }; AVLTree<int> t; for (auto e : array) t.Insert(e); t.InOreder(); cout << t.Tree_Hight() << endl; } int main() { test(); return 0; }

