PCA face recognition with Matlab
Winter vacation is coming, Mr. Wang summed up some of the things he learned in this semester, and came to share with you.
1, Theoretical knowledge basis
1. Experience sharing of some predecessors (not limited to these)
(1)PCA face recognition: a must for beginners.
(2)Understanding principal component analysis (PCA).
(3)LLE algorithm.
(4)Lagrange multiplier method.
2. Some notes and materials made by Mr. Wang
The principle data is very good. Wang made some comments. The level is not enough, everyone forgive me! ^
(1)05 - face image super-resolution reconstruction.
(2)6.5-feature extraction based on K-L transform.
(3)Matlab PCA image reduction and face matching notes.
Main data used:
- Face recognition and human motion recognition technology and application [monograph] / Cao Lin, Beijing: Electronic Industry Press, August 2015, ISBN:978-7-121-26660-7
- Pattern recognition and MATLAB implementation [monograph] / edited by Yang Jie - Beijing: Electronic Industry Press, August 2017, ISBN:978-7-121-32127-6
2, Annotation code program
1, Remodeling training data -T ()
function T = CreateDatabase(TrainDatabasePath)
%This function reshapes all 2 of the training database D The image is placed in a one-dimensional column vector.
%Then, put these one-dimensional column vectors in one row to construct 2 D Matrix " T".
%One 2 D Matrix, including all 1 D Image vector.
%Assume that all of the P Image MxN Same size.
%So the length column vector of one dimension is MN," T"will be MNxP 2D Matrix.
%%%%%%%%%%%%%%%%%%%%%%%% file management
TrainFiles = dir(TrainDatabasePath);
Train_Number = 0;
for i = 1:size(TrainFiles,1)
if not(strcmp(TrainFiles(i).name,'.')|strcmp(TrainFiles(i).name,'..')|strcmp(TrainFiles(i).name,'Thumbs.db'))
Train_Number = Train_Number + 1; % N Number of all images in the training database
end
end
%%%%%%%%%%%%%%%%%%%%%%%% One dimensional image vector to construct two dimensional matrix
T = [];
for i = 1 : Train_Number
str = int2str(i);
str = strcat('\',str,'.jpg');
str = strcat(TrainDatabasePath,str);
img = imread(str);
img = rgb2gray(img);
[irow ,icol] = size(img);
temp = reshape(img',irow*icol,1); % Will 2 D Image remodel to 1 D Image vector
T = [T temp]; % Update 2 D matrix'T'
end
2. PCA process - [m, A, Eigenfaces]
function [m, A, Eigenfaces] = EigenfaceCore(T)
%Using principal component analysis( PCA)It is determined that the features between the face images can be distinguished at most.
%%This function obtains a two-dimensional matrix, which contains all the training image vectors, and returns three outputs extracted from the training database.
%
% T - %One 2 D Matrix, including all 1 D Image vector.
% - Assume that all of the P Image MxN Same size.
% - So the length column vector of one dimension is MN," T"will be MNxP 2D Matrix.
%
% m - (M*Nx1) Training database average
% Eigenfaces - (M*Nx(P-1)) Characteristic vector of covariance matrix in training database
% A - (M*NxP) Center image vector matrix
%%%%%%%%%%%%%%%%%%%%%%%% Calculate average image
m = mean(T,2); %Calculate average face image m =(1 / P)* sum(Tj's)(j = 1: P)
Train_Number = size(T,2);
%%%%%%%%%%%%%%%%%%%%%%%% Calculate the deviation between each image and the average image
A = [];
for i = 1 : Train_Number
temp = double(T(:,i)) - m; % Computing training set Ai = Ti-m Difference image for each image in
A = [A temp]; % Merge all centered images
end
%%%%%%%%%%%%%%%%%%%%%%%% Snapshot method of feature face method
%From the theory of linear algebra, we know that for a PxQ Matrix, the maximum number of nonzero eigenvalues that the matrix can have is min(P-1,Q-1).
%Due to the number of training images( P)Usually less than the number of pixels( M * N),So the lowest eigenvalue that can be found is equal to P-1.
%So we can calculate A'* A(One PxP Matrix) instead of A * A'(One M * NxM * N Matrix).
%Obviously, A * A'Size ratio A'* A Much bigger. Therefore, the dimension will be reduced.
L = A'*A; % L It's a covariance matrix C = A * A'Substitution.
[V,D] = eig(L); %D The diagonal element of is L = A'* A and C = A * A'The characteristic value of.
%%%%%%%%%%%%%%%%%%%%%%%% Sorting and eliminating eigenvalues
%matrix L All eigenvalues of are sorted, less than the specified threshold, and are eliminated.
%Therefore, the number of non-zero eigenvectors may be less than( P-1).
L_eig_vec = [];
for i = 1 : size(V,2)
if( D(i,i)>1 )
L_eig_vec = [L_eig_vec V(:,i)];
end
end
%%%%%%%%%%%%%%%%%%%%%%%% Calculate covariance matrix'C'Eigenvector of
%Can from L Recovery covariance matrix in eigenvector of C The percentage of the feature vector of (the "feature face").
Eigenfaces = A * L_eig_vec; % A: Centered image vector
3. European distance comparison facial features - OutputName
function OutputName = Recognition(TestImage, m, A, Eigenfaces)
%This function compares two faces by projecting the image into the face space, and then measures the Euclidean distance between them.
% TestImage - Path of the picture to be detected
%
% m -(M * Nx1)Training database average
% - " EigenfaceCore"Function output.
%
% Eigenfaces - %Characteristic faces-(M * Nx(P-1))Eigenvectors
% - Percentage of covariance matrix trained
% -" EigenfaceCore"Function output.
%
% A -(M * NxP)Center image matrix
% - " EigenfaceCore"The output of the function.
%%%%%%%%%%%%%%%%%%%%%%%%Project the centered image vector into face space
%All the centered images are multiplied by the projection to the basis of the eigenfaces of the face space.
%The projection vector of each face will be its corresponding eigenvector.
ProjectedImages = [];
Train_Number = size(Eigenfaces,2);
for i = 1 : Train_Number
temp = Eigenfaces'*A(:,i);%Project the center image into the face space
ProjectedImages = [ProjectedImages temp];
end
%%%%%%%%%%%%%%%%%%%%%%%% Extract from test image PCA function
InputImage = imread(TestImage);
temp = InputImage(:,:,1);
[irow,icol] = size(temp);
InImage = reshape(temp',irow*icol,1);
Difference = double(InImage)-m; %Center test image percentage
ProjectedTestImage = Eigenfaces'*Difference; % Test image eigenvector
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Calculate the Euclidean distance percentage between the Euclidean distance projection test image and the projection calculate the percentage of all centered training images.
%The person who tested the picture should think that there is a minimum distance training database with the corresponding image in the picture.
Euc_dist = [];
for i = 1 : Train_Number
q = ProjectedImages(:,i);
temp = ( norm( ProjectedTestImage - q ) )^2;
Euc_dist = [Euc_dist temp];
end
[ ~,Recognized_index] = min(Euc_dist);
OutputName = strcat(int2str(Recognized_index),'.jpg');
4. Use example - Example
% Clear variables
clear all
clc
close all
% Customize and set initial directory path
TrainDatabasePath = uigetdir('F:\Matlab_2016b_64bit\code_matlab\face\face_test\code', 'Select training database path' );
TestDatabasePath = uigetdir('F:\Matlab_2016b_64bit\code_matlab\face\face_test\code', 'Select test database path');
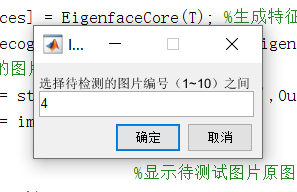
prompt = {'Select the picture number to be tested (1~10)Between'};
%Select the picture to be matched, and enter the known library to search for matching
dlg_title = 'Input of PCA-Based Face Recognition System';
num_lines= 1;
def = {'1'};
TestImage = inputdlg(prompt,dlg_title,num_lines,def);
TestImage = strcat(TestDatabasePath,'\',char(TestImage),'.jpg');
%Each cycle TestImage All that remains is TestDatabasePathTest\TestImage.jpg
im = imread(TestImage);
%Returned array A Contains image data.
%If the file contains a gray image, A yes M*N If the file contains a true color image, A yes M*N*3 The array.
% Create face database
T = CreateDatabase(TrainDatabasePath); %Generate 2D matrix based on training picture path
[m, A, Eigenfaces] = EigenfaceCore(T); %Generating characteristic quantity
OutputName = Recognition(TestImage, m, A, Eigenfaces);
% Select the picture you want to recognize
SelectedImage = strcat(TrainDatabasePath,'\',OutputName);
SelectedImage = imread(SelectedImage);
% display picture
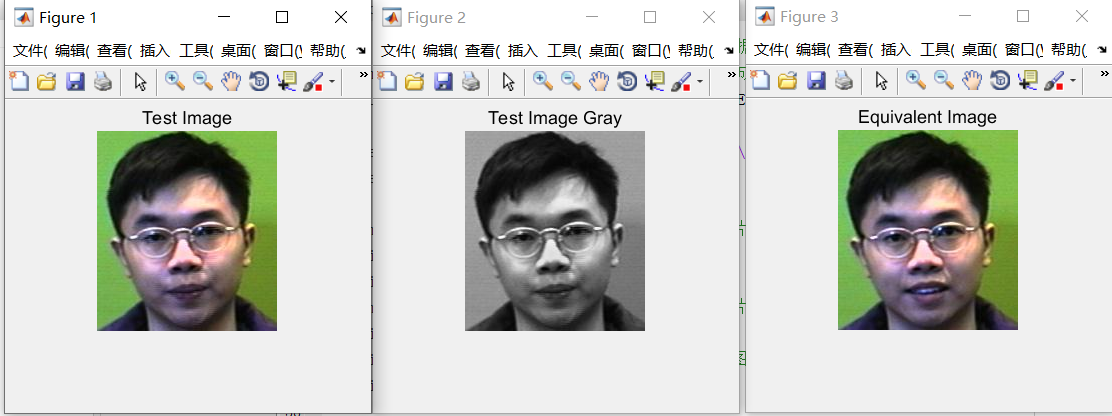
imshow(im) %Display the original picture of the picture to be tested
title('Test Image');
figure,im1=rgb2gray(im);
imshow(im1); %Display the gray scale of the picture to be tested
title('Test Image Gray');
figure,imshow(SelectedImage);%Show matching pictures
title('Equivalent Image');
str = strcat('Matched image is : ',OutputName);
disp(str)
3, Use process
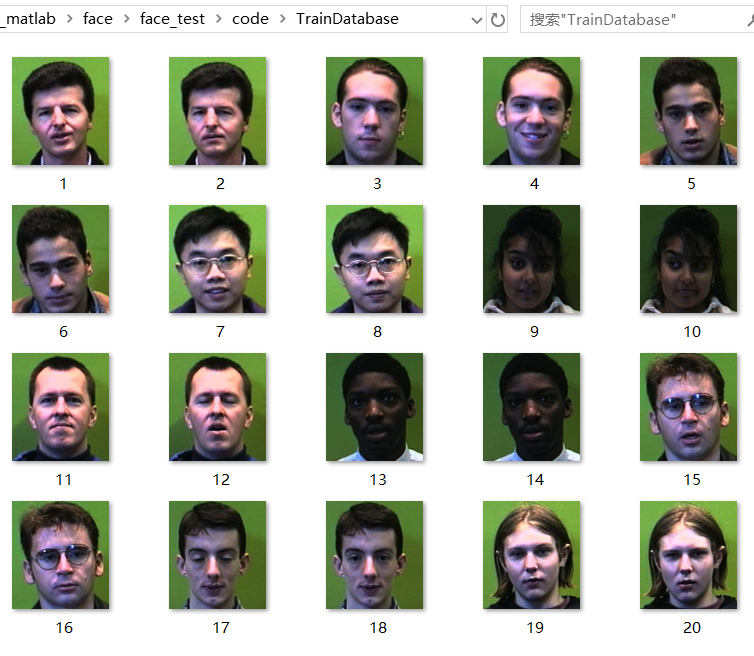
1. Select training dataset
- Training data set:
2. Select test data set
- Test data set
- Is it a little bit confusing for some beautiful man who flashes in? Let's explain the significance of his existence later
(of course, it's to give me the motivation to keep fit, hehe ~)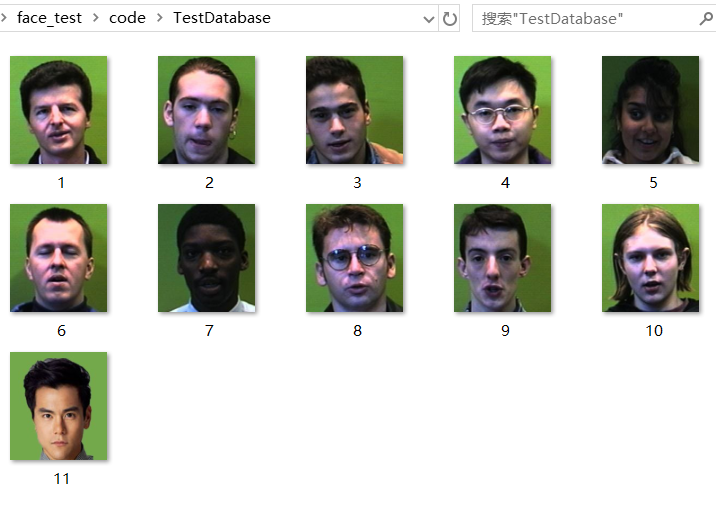
- Is it a little bit confusing for some beautiful man who flashes in? Let's explain the significance of his existence later
3. Select face image number to be detected
4. Output matching results
Four. Follow up
Did we forget the man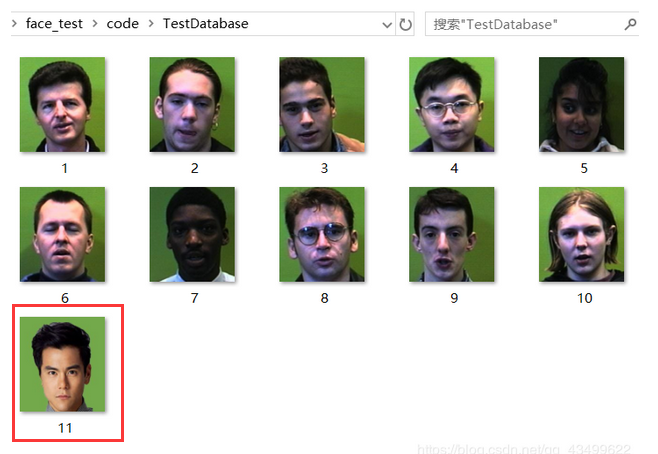 What does he mean to us? (in addition to eye care and motivation to lose weight...)
What does he mean to us? (in addition to eye care and motivation to lose weight...)
Let's get this project running again
To select the test picture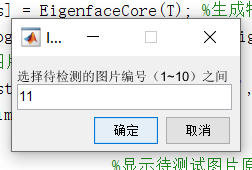
Let's take a look at the results
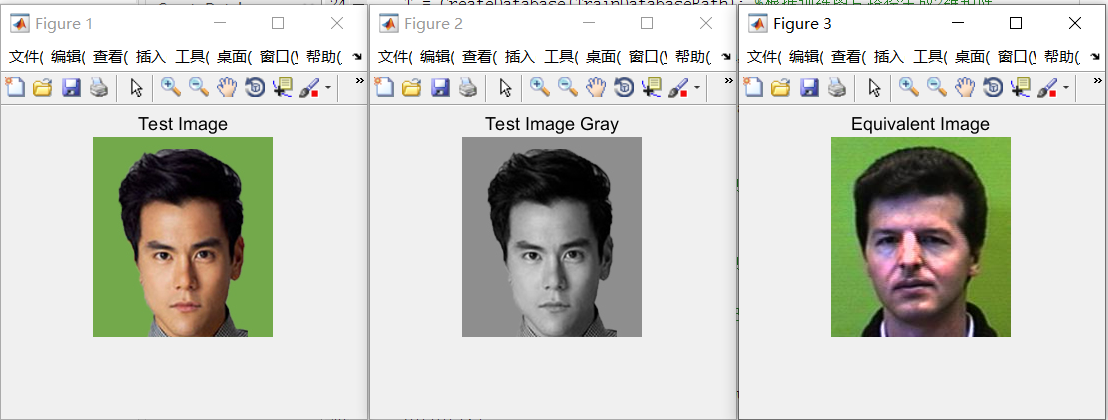 Shock!!! Why does brother Peng, who has sharp edges and corners, become a greasy uncle??? (the years are not so merciless...)
Shock!!! Why does brother Peng, who has sharp edges and corners, become a greasy uncle??? (the years are not so merciless...)
Very simply, let's look back at the contents of the two datasets
You will find that there is no brother Peng Yuyan in our training center
If you really understand the principle of PCA dimension reduction
You will understand that PCA will select the image (training set) output that is closest to the European distance of the input image (test set) data based on the data characteristics of the average face
Therefore, we have to admit that this uncle's facial data is the "most suitable" facial data feature of the male god
//So it's not hard to understand why so many software and enterprises want your facial data now to provide data for their training models
//The dataset used by Mr. Wang is Yale University's open-source face data. You can also use PS software to create the face dataset for learning. The image attributes are: 200 * 200 pixels, green background.
//The level is limited. I'm sorry, everyone. (hugging...)

