Reference resources: https://blog.csdn.net/android_heng/article/details/76599302

Binary tree building includes: root node, left child, right child, data

It is defined as follows:

BinTree root;
BinTree lChild;
BinTree rChild;
Object data;
List<BinTree> datas;

The method of building binary tree:

public void CreateTree(Object[] objs){
		datas = new ArrayList<BinTree>();
		for(Object obj : objs){
			datas.add(new BinTree(obj));
		}
		root = datas.get(0);
		for(int i=0;i<datas.size()/2;i++){
			datas.get(i).lChild = datas.get(2*i+1);
			if((2*i+2)<datas.size()){
				datas.get(i).rChild = datas.get(2*i+2);
			}
		}
	}

Traversal of binary tree:

1: Preorder traversal (DLR)

1): access the root node;

2): traverse and access the left subtree in order

3): traverse and access the right subtree in order

//Preorder traversal
	public void preOrder(BinTree root){
		if(root!=null){
			visit(root.getdata());
			preOrder(root.getlchild());
			preOrder(root.getrchild());
		}
	}

2: Middle order traversal (LRD)

1): traverse left subtree in middle order

2): access root node

3): traverse and access the right subtree in medium order

//Sequential traversal
public void inOrder(BinTree root){
	if(root!=null){
		inOrder(root.getlchild());
		visit(root.getdata());
		inOrder(root.getrchild());
	}
}

3: Postorder ergodic

1): traverse and access the left subtree in a later order

2): traverse and access the right subtree in a later order

3): access root node

//Post order traversal
public void afterOrder(BinTree root){
	if(root!=null){
		afterOrder(root.lChild);
		afterOrder(root.rChild);
		visit(root.getdata());
	}
}

The complete code of binary tree establishment and traversal is as follows:

class BinTree{
    BinTree root;
    BinTree lChild;
    BinTree rChild;
    Object data;
    List<BinTree> datas;
    
    public BinTree(BinTree lChild,BinTree rChild,Object data){
        super();
        this.lChild = lChild;
        this.rChild = rChild;
        this.data = data;
    }
　　//First, give the data to the node, set the left and right subtrees of the node to be empty, and then allocate the left and right subtrees
    public BinTree(Object data){
        this(null,null,data);
    }
    public BinTree(){
        super();
    }
    
    public Object getdata(){
        return this.data;
    }
    public BinTree getlchild(){
        return this.lChild;
    }
    public BinTree getrchild(){
        return this.rChild;
    }
    //Building a binary tree
    public void CreateTree(Object[] objs){
        datas = new ArrayList<BinTree>();
        for(Object obj : objs){
            datas.add(new BinTree(obj));
        }
        root = datas.get(0);
        for(int i=0;i<datas.size()/2;i++){
            datas.get(i).lChild = datas.get(2*i+1);
            if((2*i+2)<datas.size()){
                datas.get(i).rChild = datas.get(2*i+2);
            }
        }
    }
    //Preorder traversal
    public void preOrder(BinTree root){
        if(root!=null){
            visit(root.getdata());
            preOrder(root.getlchild());
            preOrder(root.getrchild());
        }
    }
    //Sequential traversal
    public void inOrder(BinTree root){
        if(root!=null){
            inOrder(root.getlchild());
            visit(root.getdata());
            inOrder(root.getrchild());
        }
    }
    //Post order traversal
    public void afterOrder(BinTree root){
        if(root!=null){
            afterOrder(root.lChild);
            afterOrder(root.rChild);
            visit(root.getdata());
        }
    }
    
    public void visit(Object obj){
        System.out.print(obj+" ");
    }
    public BinTree getroot(){
        return this.root;
    }
}

Test code:

public class BinaryTree {
    public static void main(String[] args){
        BinTree binTree = new BinTree();
        Object[] num = {34,56,2,56,8745,33,76,445};
        binTree.CreateTree(num);
        System.out.print("Preorder traversal:");
        binTree.preOrder(binTree.getroot());
        System.out.print("\n"+"Middle order traversal:");
        binTree.inOrder(binTree.getroot());
        System.out.print("\n"+"Subsequent traversal:");
        binTree.afterOrder(binTree.getroot());
    }
}

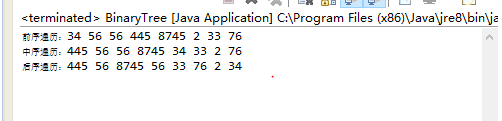
Result: