Network flows, which are closely related to linear programming, are a kind of specific flow solution. The theory and application of network flow are developing. And what we are going to talk about today is a common problem in the network flow - the biggest flow problem.

Maximum flow problem, a combinatorial optimization problem, is to discuss how to make full use of the capacity of the device to maximize the flow of transportation, so as to achieve the best results. The labeling algorithm for maximum flow was first proposed by Ford and Foxon in 1956. The "network flow theory" established by Ford and Fulkerson in 1950s is an important component of network application.

Before solving this problem, we need to understand some definitions:

The network flow graph is a directed graph with only one source point and sink point, and the maximum flow is to find the maximum water flow between the source point and sink point. The problem in the figure below is the most basic and classic maximum flow problem

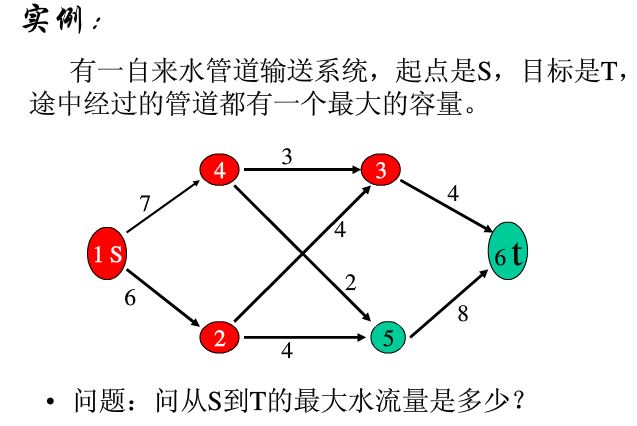
2, Flow, capacity and feasible flow

For arc (u,v), flow is the amount of water flowing on it (we usually use f(u,v)), while capacity is the maximum amount of water that can flow on it (we usually use c(u,v)). As long as f(u,v) < = c(u,v), we call flow f(u,v) is feasible flow (for maximum flow problem, flow on all pipes must be feasible flow).

3, Zengguang Road

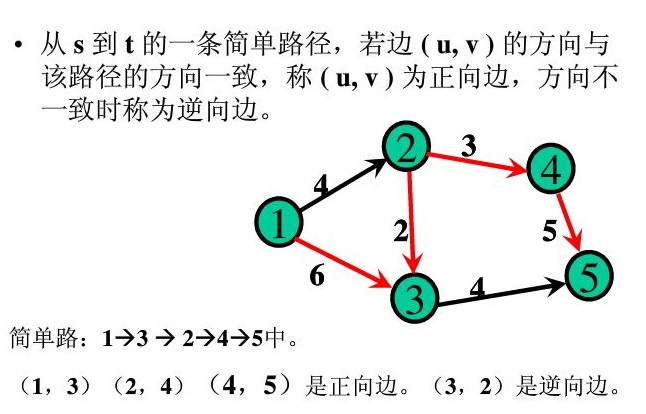
If all sides of a road meet:

Then we call this path an augmentation path, or augmentation path for short.

Now that you understand some definitions, you can introduce the famous Ford Fulkerson algorithm.

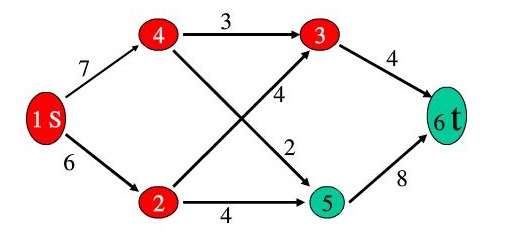
As shown in the figure, if we find an augmentation path every time, as long as the augmentation path passes through the confluence point, it means that the water flow can be increased at this time, and the increased amount is d(d=min(d,c(u,v)-f(u,v)) or D = min (D, f (U, V)).

It can be understood that for each positive edge, the maximum flow he can add is c(u,v)-f(u,v). For the reverse side, when the flow on the forward side increases, the reverse flow on the reverse side will decrease, and the maximum amount of water that can be reduced is f(u,v). Since we want to ensure that all f(u,v) is feasible after adding water flow, we take the minimum value.

After the increase, we need to update the traffic, each positive side + d, and each negative side - d.

In this case, our thinking is as follows:

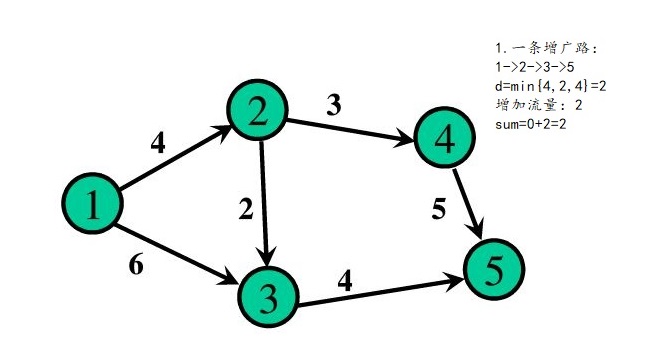
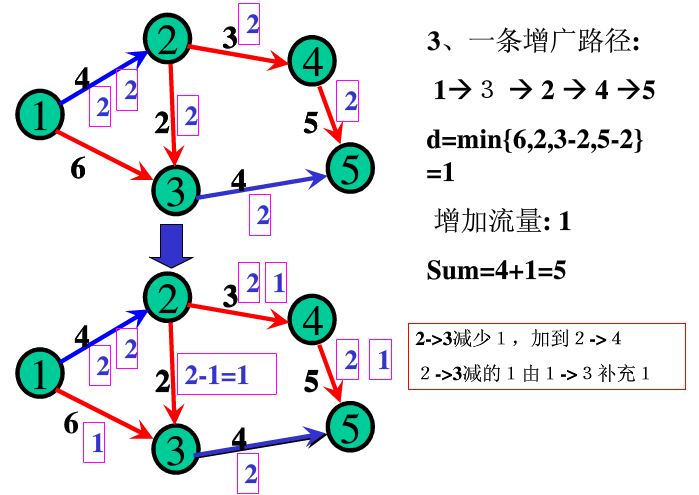
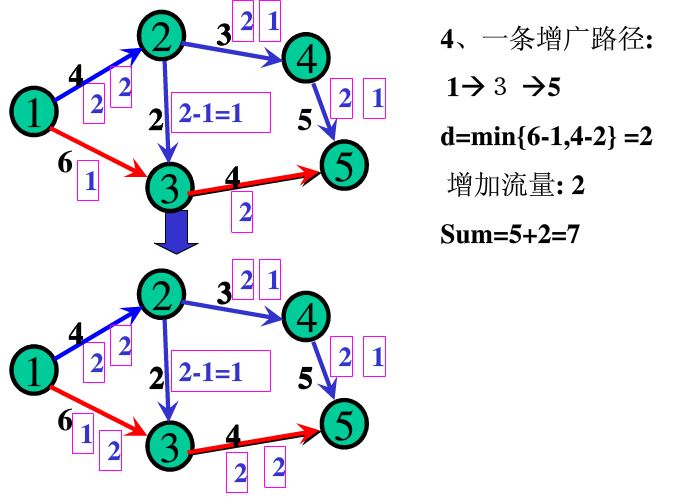
Then the code above:

#include<bits/stdc++.h>
#include<vector>
#define maxn 1200
#define INF 2e9
using namespace std;
int i,j,k,n,m,h,t,tot,ans,st,en;
struct node{
    int c,f;
}edge[maxn][maxn];
int flag[maxn],pre[maxn],alpha[maxn],q[maxn],v;
int read(){
    char c;int x;while(c=getchar(),c<'0'||c>'9');x=c-'0';
    while(c=getchar(),c>='0'&&c<='9') x=x*10+c-'0';return x;
}

void bfs(){
    memset(flag,0xff,sizeof(flag));memset(pre,0xff,sizeof(pre));memset(alpha,0xff,sizeof(alpha));
    flag[st]=0;pre[st]=0;alpha[st]=INF;h=0,t=1;q[t]=st;
    while(h<t){
        h++;v=q[h];
        for(int i=1;i<=n;i++){
            if(flag[i]==-1){
                if(edge[v][i].c<INF&&edge[v][i].f<edge[v][i].c){
                    flag[i]=0;pre[i]=v;alpha[i]=min(alpha[v],edge[v][i].c-edge[v][i].f);q[++t]=i;
                }
                else if(edge[i][v].c<INF&&edge[i][v].f>0){
                    flag[i]=0;pre[i]=-v;alpha[i]=min(alpha[v],edge[i][v].f);q[++t]=i;
                }
            }
        }
        flag[v]=1;
    }
}

void Ford_Fulkerson(){
    while(1){
        bfs();
        if(alpha[en]==0||flag[en]==-1){
            break;
        }
        int k1=en,k2=abs(pre[k1]);int a=alpha[en];
        while(1){
            if(edge[k2][k1].c<INF) edge[k2][k1].f+=a;
            else if(edge[k1][k2].c<INF) edge[k1][k2].f-=a;
            if(k2==st) break;
            k1=k2;k2=abs(pre[k1]);
        }
        alpha[en]=0;
    }
}

void flow(){
    int maxflow=0;
    for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++){
        if(i==st&&edge[i][j].f<INF) maxflow+=edge[i][j].f;
      }
    printf("%d",maxflow);
}

int main(){
    int u,v,c,f;
    n=read();m=read();st=read();en=read();
    for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++) edge[i][j].c=INF,edge[i][j].f=0;
    for(int i=1;i<=m;i++){
        u=read();v=read();c=read();
        edge[u][v].c=c;
    }
    Ford_Fulkerson();
    flow();
    return 0;
}