The function of softmax

    for classification, the function of softmax is to calculate the probability that the sample belongs to each category from the sample value. For example, for handwritten numeral recognition, softmax model obtains the probability values of 0-9 from the given pixel value of handwritten image, and the sum of these probability values is 1. The predicted results take the number represented by the maximum probability as the classification of this picture.

You can understand softmax from the following figure

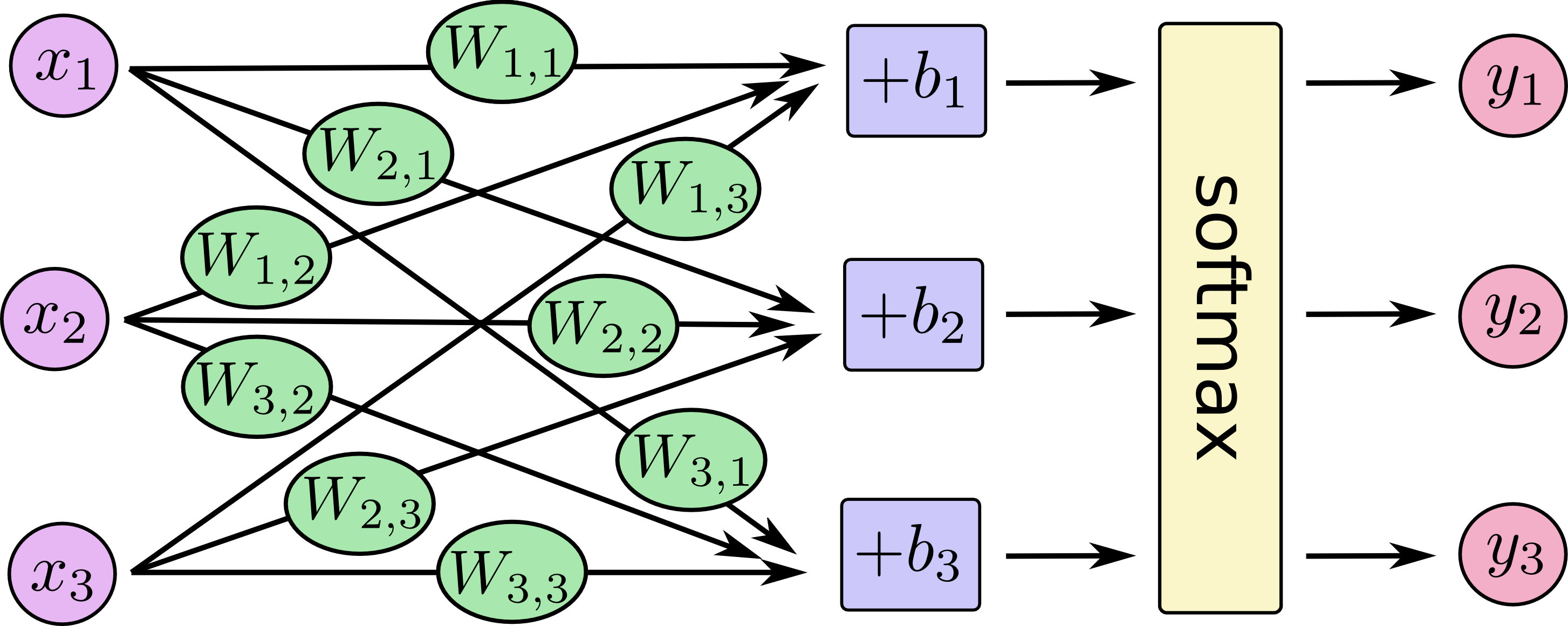
x1,x2,x3 represent the input value, b1,b2,b3 represent the offset of category 1, 2, 3, because the input value may have irrelevant interference.
Write the figure above as an equation
\[ \left[\begin{matrix}temp_1\\temp_2\\temp_3\end{matrix}\right] =\left(\begin{matrix}W_{1,1}x_1+W_{1,2}x_2+W_{1,3}x_3+b_1\\ W_{2,1}x_1+W_{2,2}x_2+W_{2,3}x_3+b_2\\ W_{3,1}x_1+W_{3,2}x_2+W_{3,3}x_3+b_3\end{matrix}\right)\\ \left[\begin{matrix}y_1\\y_2\\y_3\end{matrix}\right] =softmax\left(\begin{matrix}temp_1\\ temp_2\\ temp_3\end{matrix}\right)\\ Where y_i = softmax (temp_i) = \ frac {exp (temp_i)} {\ sum {J = 0} ^ {n} exp (temp_j)}}\ Y ﹣ 1, y ﹣ 2, y ﹣ 3, respectively, represent the probability value that the sample belongs to category 1, 2, 3. \]
   in neural network, the accuracy of classification is improved by training the weight value W and the bias value b in the training set training model.
(the training method is to define a loss function (representing the difference between the predicted value and the real value), and then use the gradient descent method (by calculating the partial derivative of W and b) to minimize the loss function. The specific process is a little complicated. The following is just to directly use the tensorflow function to realize, and then supplement the principle if there is time.)

Handwritten digit recognition with Tensorflow

First, import the mnist data set from tensorflow, which contains the pixel matrix of handwritten digital pictures and the corresponding number categories of these pictures:

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

Explain that the pixel matrix of the picture is a vector that flattens 28x28 to the size of [1x784]; the label is a vector of [1x10], where one number is 1 and the rest are all 0. For example, if the label represents the number 5, the label vector is [0,0,0,0,1,0,0,0,0,0,0,0].
Build the model:

x = tf.placeholder("float",[None,784])
#A placeholder for a two-dimensional vector. None indicates that the first digit can be any length. 784 indicates the flattened length of an image
W = tf.Variable(tf.zeros([784,10]))
b = tf.Variable(tf.zeros([10]))

#temp = x*W + b
#softmax(temp) gets a vector of [None,10], indicating that None pictures may represent the probability of 0-9.
y = tf.nn.softmax(tf.matmul(x,W)+b)

Building the model training process: define the loss function, minimize the loss function, and get W, b

y_ = tf.placeholder("float",[None,10])
#Here, placeholders are used to represent y (the real category of each picture), and the real category will be filled in to the placeholders later.
cross_entropy = -tf.reduce_sum(y_*tf.log(y))
#Y is the prediction category of the model, y UU is the real category, and the cross entropy is used to represent the loss function (explain the difference between the predicted value and the real value)
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)
#Using gradient descent method to minimize loss function

Run the previously constructed model:

init = tf.initialize_all_variables()#init means to initialize all variables
sess = tf.Session()#Start a session to run the model
sess.run(init)#Running init really initializes all variables
for i in range(1000):#Training Model 1000 times
    batch_xs,batch_ys = mnist.train.next_batch(100)
    #Take 100 samples from the dataset
    sess.run(train_step, feed_dict={x:batch_xs, y_:batch_ys})
    #Fill the sample with the placeholders you defined before, and then run the training process you just built

Evaluation model:

correct_prediction = tf.equal(tf.argmax(y,1),tf.argmax(y_,1))
#Judge whether the predicted value and the real value are equal one by one, and return a matrix.
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
#tf.cast converts bool type to float type, and reduces the mean value (i.e. accuracy rate)
print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))
#Fill the test set with the previous placeholder, run the previous model, and get the accuracy rate

The output result is:
0.9181

summary

                        . Users don't need to program and realize the specific operation step by step, which makes the construction of neural network much easier.

We are learning the notes written by tensorflows. Welcome to comment and discuss!

Reference website: tensorflow Chinese community