Title Link: Doraemon portal

Meaning: girls have a beauty level of B1, intelligence level of I1, boys have a handsome level of B2, intelligence level of I2.

Now there are n boys and m girls. You need to find the most suitable boy for m girls. One boy can be selected by multiple girls.

The suitability of girls and boys is:

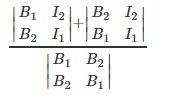
To simplify:It can be seen that it is actually the direct slope between the girl point and the boy point.

We first arrange all the points in order (first by x, then by y), and then we make a lower convex hull for these boy points. When we meet a girl point, we construct a lower convex hull just before the girl point to divide a boy point with the largest slope. Why do we need to lower the convex hull instead of the upper convex hull? Because when we meet a girl point, we always find a point on the left, making the slope the most Big, then he should try his best to look down.

What we are looking for above is a boy's point for each girl on the left side of the point, but it's possible that the best boy's point for this girl is not on the left side, but on the right side, so we need to lower the convex hull again, this time from the back.

Figure 1: see code Figure 2: see code

The code program refers to the official program.

#include<bits/stdc++.h>

using namespace std;

typedef long long LL;

const int maxn=200010;

struct point{

    LL x,y;///Coordinates of points
    int id,flag; ///id indicates the position of this point, flag=1 indicates that this point is a boy point, and flag=2 indicates a girl point
    point(){}
    point(LL _x,LL _y,int _id,int _flag){
        x=_x;y=_y;id=_id;flag=_flag;
    }

    bool operator < (const point &b){
    return x==b.x?y<b.y:x<b.x;
    }
}p[maxn],ch[maxn],ans1[maxn],ans2[maxn];

int pos[maxn],tot;

point operator + (point a,point b){ return point(a.x+b.x,a.y+b.y,0,0);}
point operator - (point a,point b) {  return point(a.x-b.x,a.y-b.y,0,0);}




LL cross(point a,point b){  return a.x*b.y-a.y*b.x;}

///Ex boyfriend, girl, present boyfriend
bool judge(point a,point b,point c){
    LL item=cross(a-b,c-b);

    ///For both, choose the youngest boyfriend
    return item==0?c.id<a.id:item<0;
}

void andrew(int n)
{
    tot=-1;

    for(int i=0;i<n;i++)
    {
        ///When you meet a boy
        if(p[i].flag==1){
        while(tot>0&&cross(ch[tot]-ch[tot-1],p[i]-ch[tot-1])<0)
            tot--;
        ch[++tot]=p[i];
        }
        else{

            if(tot==-1) continue;
            int l=0,r=tot;
            ///Finding the optimal point of convex hull under dichotomy
            while(l<r)
            {
                int mid=(l+r)>>1;
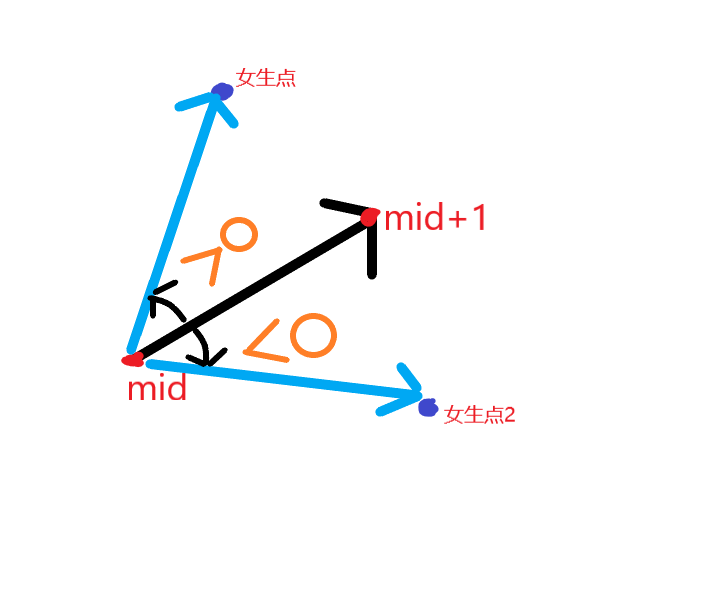
                    /// see Figure 1
                if(cross(ch[mid+1]-ch[mid],p[i]-ch[mid])>0)
                    l=mid+1;
                else r=mid;
            }
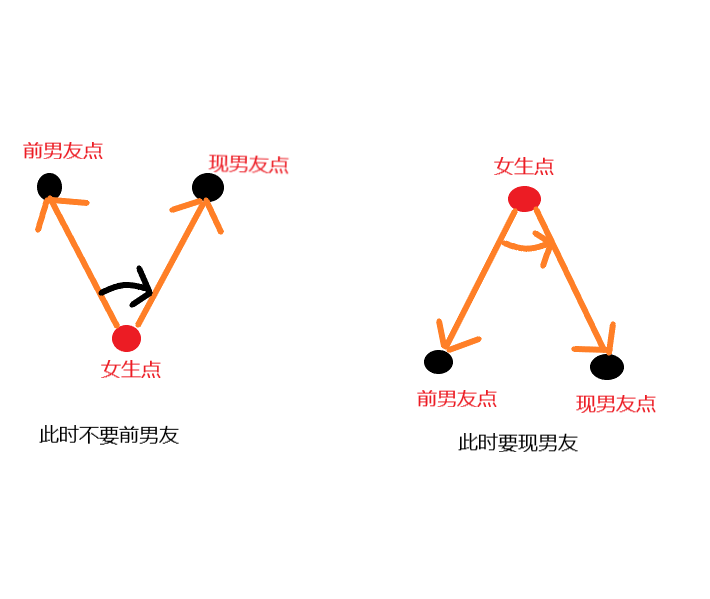
                ///If the girl hasn't been matched, give her the boy directly. To match, compare the two boys
            if(pos[p[i].id]==-1||judge(ans1[pos[p[i].id]],ans2[p[i].id],ans1[ch[l].id]))
                pos[p[i].id]=ch[l].id;
        }
    }
}

int main()
{

    int n,m;
    LL x1,y1;
    scanf("%d%d",&n,&m);

    for(int i=0;i<n+m;i++)
    {
        scanf("%lld%lld",&x1,&y1);
        if(i<n){
                ///ans1 stores boys' points
            ans1[i]=point(x1,y1,i,1);
            p[i]=ans1[i];///p store all points
        }
        else{
            ///ans2 stores girls' points
            ans2[i-n]=point(x1,y1,i-n,2);
            p[i]=ans2[i-n];
        }
    }

    memset(pos,-1,sizeof(pos));
    ///Sort all points
    sort(p,p+n+m);

    ///For the first time, lower the convex hull and find the best boy point on the left side of the girl point
    andrew(n+m);


    ///For the second time, find the best boy point on the right side of the girl point
    ///Flip and reverse all coordinates
    reverse(p,p+n+m);
    for(int i=0;i<n+m;i++)
    {
        p[i].x=-p[i].x;
        p[i].y=-p[i].y;
    }
    andrew(n+m);

    for(int i=0;i<m;i++)
        printf("%d\n",pos[i]+1);


    return 0;
}

My tag: be a passionate programmer.