Merge order:

1. It is a sort algorithm based on merge operation, which is an application of divide and conquer method

2. Steps:

Assume that the sequence to be sorted is R[0...n-1], and adopt two-way merge

a. divide r into two subsequences R1, R2 with the same growth or the same difference of 1

b. divide the subsequences R1 and R2 recursively until the length of the subsequence is 1

c. merge subsequences with two pairs, and sort them at the same time until the sequence length is n, for example, merge [1, 4] and [2, 3] = = > [1, 2, 3, 4]

Note: n-way merging divides the sequence into n subsequences, generally n = 2

The divide and conquer method is to divide the problem instances into several sub instances, and solve each sub instance recursively, and then combine the solutions of these sub instances to get the solution of the original problem instance

void merge(std::vector<int>& nums, int left, int mid, int right)
{
    
    int len = right - left + 1;
    int* temp = new int[len];       // Auxiliary space O(n)
    int index = 0;
    int i = left;                   // Start subscript of previous array 
    int j = mid + 1;                // Starting subscript of the next array 
    
    while (i <= mid && j <= right) {
//        Choose the smaller one 
        temp[index++] = nums[i] <= nums[j] ? nums[i++] : nums[j++];
    }
//    Put all the subsequences that are not put back to the auxiliary space back (because of divide and conquer, the subsequences are already sorted) 
    while (i <= mid) {
        temp[index++] = nums[i++];
    }
    while (j <= right) {
        temp[index++] = nums[j++];
    }
//    Deep copy 
    for (int k = 0; k < len; k++) {
        nums[left++] = temp[k];
    }
//    Use new The space created by the keyword is in the heap and needs to be deleted actively, while the usual variable declaration is usually in the stack, which is automatically deleted and freed by the computer 
    delete temp;
}

void mergeSort(std::vector<int>& nums, int left, int right)
{
    if (left >= right)
        return ;
    int mid = (left + right) / 2;
    mergeSort(nums, left, mid);
    mergeSort(nums, mid+1, right);
    merge(nums, left, mid, right);
}

Note: for deep copy, the address of the pointer is different, but the content is the same; for shallow copy, not only the value is the same, but also the address of the pointer is the same, which will be affected by the change of the original content

Heap sort:

1. Nature of reactor:

a. in the data structure, the heap is an approximate complete binary tree. Except for the bottom layer, the heap is full (note the difference between full binary tree and full binary tree)

b. each node of the tree corresponds to an element in the array, and its root node corresponds to an element with a subscript of 0

c. The subscript of the parent node is (i + 1) / 2-1, the subscript of the left child is 2*i + 1, and the subscript of the right child is 2*i + 2

d. in the maximum heap, the value of the parent node must be greater than that of its child node, while the minimum heap must be less than

2. Steps:

a. build the maximum heap. See the code for details

b. take out the first element (maximum value) of the maximum heap, then put the last element in the position with the subscript of 0, and readjust the maximum heap (as shown below)

c. repeat operation b until the first element, when the heap has become the minimum heap

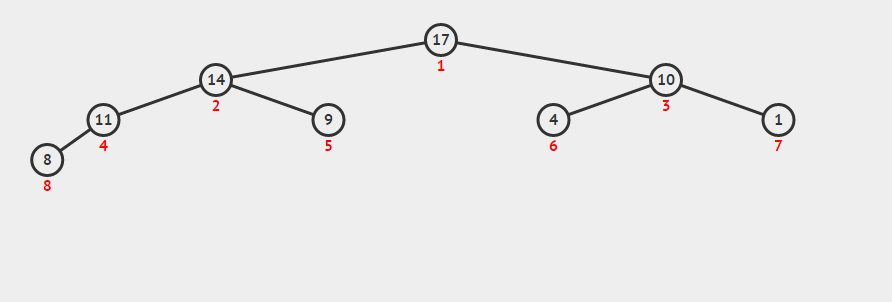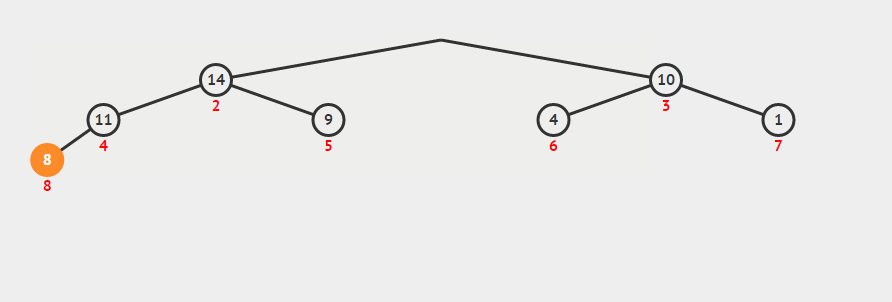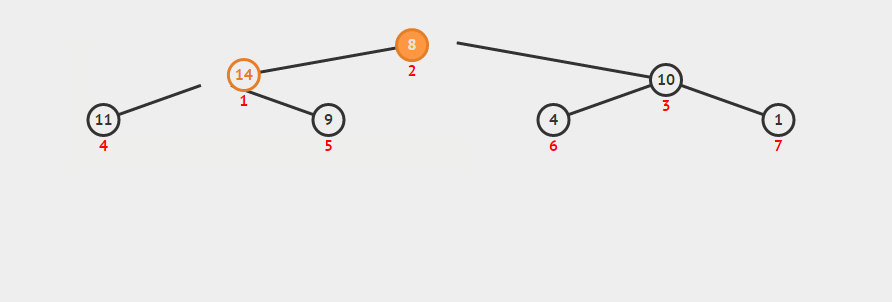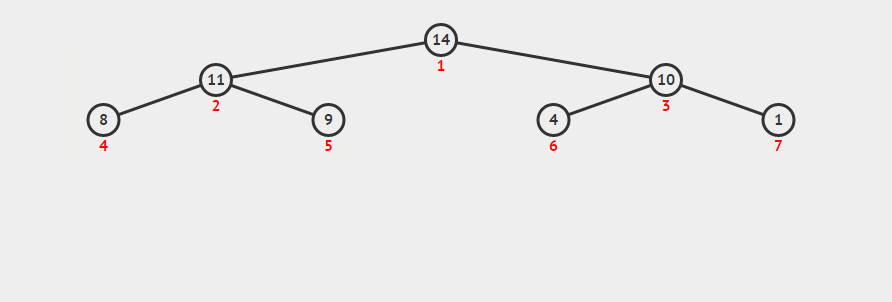
//Downward adjustment 
void siftDown(std::vector<int>& nums, int star, int last_index)
{
    int i = star;
    int j = i * 2 + 1;
//    Record nodes to adjust 
    int temp = nums[i];
    while (j <= last_index) {
//        Record the larger child node 
        if (j < last_index && nums[j] < nums[j+1])
            j++;
//        If the parent node is greater than or equal to the largest child node, exit the loop, otherwise exchange the two nodes 
        if (temp >= nums[j])
            break;
        else {
            nums[i] = nums[j];
//            Look down for child nodes 
            i = j;
            j = 2 * j +1;
        }
    }
//    After the end of the cycle i The position of is the new position of the node to be adjusted 
    nums[i] = temp;
}

void heapSort(std::vector<int>& nums)
{
    int len = nums.size();
//    Build the maximum heap, note that it is minus 2, because the last node must be a child node 
    for (int i = (len - 2) / 2; i >= 0; --i) {
        siftDown(nums, i, len-1);
    }
    //Making the largest heap the smallest by swapping 
    for (int i = len-1; i >= 0; --i){
        //The exchange header and subscript are i Elements 
        int t = nums[0];
        nums[0] = nums[i];
        nums[i] = t;
        //Exclude the largest element and refactor the largest heap 
        siftDown(nums, 0, i-1);
    }
}

Note: when using the minimum heap, we can only ensure that the parent node is larger than the child node, but not the size relationship of the sibling node. Therefore, we build the maximum heap first, and then sort the heap

The main functions of the above two sorting algorithms are the same as those of the previous bubble sorting