http://poj.org/problem?id=1039

The GX Light Pipeline Company started to prepare bent pipes for the new transgalactic light pipeline. During the design phase of the new pipe shape the company ran into the problem of determining how far the light can reach inside each component of the pipe. Note that the material which the pipe is made from is not transparent and not light reflecting.

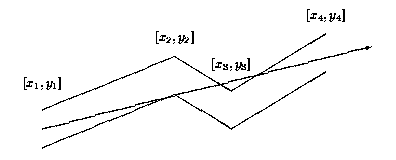
Each pipe component consists of many straight pipes connected tightly together. For the programming purposes, the company developed the description of each component as a sequence of points [x1; y1], [x2; y2], . . ., [xn; yn], where x1 < x2 < . . . xn . These are the upper points of the pipe contour. The bottom points of the pipe contour consist of points with y-coordinate decreased by 1. To each upper point [xi; yi] there is a corresponding bottom point [xi; (yi)-1] (see picture above). The company wants to find, for each pipe component, the point with maximal x-coordinate that the light will reach. The light is emitted by a segment source with endpoints [x1; (y1)-1] and [x1; y1] (endpoints are emitting light too). Assume that the light is not bent at the pipe bent points and the bent points do not stop the light beam. 

Input
The input file contains several blocks each describing one pipe component. Each block starts with the number of bent points 2 <= n <= 20 on separate line. Each of the next n lines contains a pair of real values xi, yi separated by space. The last block is denoted with n = 0.
Output
The output file contains lines corresponding to blocks in input file. To each block in the input file there is one line in the output file. Each such line contains either a real value, written with precision of two decimal places, or the message Through all the pipe... The real value is the desired maximal x-coordinate of the point where the light can reach from the source for corresponding pipe component. If this value equals to xn, then the message Through all the pipe. will appear in the output file.
Sample Input

4
0 1
2 2
4 1
6 4
6
0 1
2 -0.6
5 -4.45
7 -5.57
12 -10.8
17 -16.55
0

Sample Output

4.67
Through all the pipe.

Give a pipeline, its width is 111, the starting coordinate is (x1, y1) (x {1}, y {1} (x1, y1}) (x1, y1). There are many turning points i n this pipeline. Give the coordinates (x i, yi) (x {i}, y {i} (xi,yi), (xi,yi) for the turning point of the upper layer (xi,yi), (xi,yi) (x {u{i}, y {i}) (xi,yi) for the turning coordinates of the lower layer is (xi, Yiyi) (x {{i}, y {i}, y {{i}-1 {-1 u {n}, y {n} (xn) (yn), now there are numerous rays from the pipe entrance, the light will not reflect, will not refract, ask the farthest reach of the abscissa. If you can cross the pipe, output Through all the pipe. Through all the pipe. Throughall the pipe.
Thought: A straight line that can reach the farthest point must pass through a bend point of the upper pipeline wall and a bend point of the lower pipeline wall. So we can enumerate the fold points and connect the upper and lower bends of the same abscissa coordinate into a line segment to see if the line segment composed of the folds we enumerate intersects with the line segment or not. If all the lines intersect with nnn, then the light can pass through the whole pipeline. Otherwise, if the straight line does not want to intersect with the first k k k line segment, then the straight line either shoots on the pipeline on the k_1k-1k_1 block or on the pipeline under the k_1k-1k_1 block, and calculates the maximum abscissa coordinates at the intersection points of the two cases respectively.

#include<iostream>
#include<cstdio>
#include<cmath>
#include<vector>
#include<algorithm>
#include<cstring>
using namespace std;

const double pi=acos(-1.0);//Radian pi
const double eps=1e-10;//accuracy

struct point
{
    double x,y;
    point(double a=0,double b=0)
    {
        x=a,y=b;
    }
    friend point operator * (point a,double b)
    {
        return point(a.x*b,a.y*b);
    }
    friend point operator * (double a,point b)
    {
        return point(b.x*a,b.y*a);
    }
    point operator - (const point &b)const
    {
        return point(x-b.x,y-b.y);
    }
    point operator + (const point &b)const
    {
        return point(x+b.x,y+b.y);
    }
    point operator / (const double b)const
    {
        return point(x/b,y/b);
    }
    bool operator < (const point &b)const//Sort by coordinates
    {
        if(fabs(x-b.x)<eps)
            return y<b.y-eps;
        return x<b.x-eps;
    }
    void transxy(double sinb,double cosb)//Counterclockwise rotation b radian
    {                                      //If a - is added clockwise before the incoming sinb
        double tx=x,ty=y;
        x=tx*cosb-ty*sinb;
        y=tx*sinb+ty*cosb;
    }
    void transxy(double b)//Counterclockwise rotation b radian
    {                     //If clockwise - b
        double tx=x,ty=y;
        x=tx*cos(b)-ty*sin(b);
        y=tx*sin(b)+ty*cos(b);
    }
    double norm()
    {
        return sqrt(x*x+y*y);
    }
};

inline double dot(point a,point b)//Dot product
{
    return a.x*b.x+a.y*b.y;
}
inline double cross(point a,point b)//Cross product
{
    return a.x*b.y-a.y*b.x;
}

inline double dist(point a,point b)//Distance between two points
{
    return (a-b).norm();
}

inline int sgn(double x)
{
    if(fabs(x)<eps)
        return 0;
    if(x>0)
        return 1;
    return -1;
}

typedef point Vector;

struct line
{
    point s,e;
    line(){}
    line(point _s,point _e)
    {
        s=_s,e=_e;
    }
};

double xmult(point p1,point p2,point p3)//p1p2 X p1p3
{
    return cross(p2-p1,p3-p1);
}

bool seg_inter_line(line l1,line l2)//Judging whether line l1 intersects line segment l2
{
    return sgn(xmult(l2.s,l1.s,l1.e))*sgn(xmult(l2.e,l1.s,l1.e))<=0;
}

inline double dis_point_seg(point p,line l)//Calculate the distance between point and line segment
{
    if(sgn(dot(p-l.s,l.e-l.s))<0)//There is no distance from the return point to the end of the line segment.
        return (p-l.s).norm();
    if(sgn(dot(p-l.e,l.s-l.e))<0)//There is no distance from the return point to the end of the line segment.
        return (p-l.e).norm();
    return fabs(cross(l.s-p,l.e-p))/dist(l.s,l.e);//| Cross product |= 2*S Delta
}

void popint_proj_line(point p,point s,point t,point &cp)//The vertical foot of calculating point p to line segment st is stored in cp
{
    double r=dot(t-s,p-s)/dot(t-s,t-s);
    cp=s+r*(t-s);
}

bool point_on_seg(point p,point s,point t)//Determine whether point p includes endpoints on line segment st
{
    return sgn(cross(p-s,t-s))==0&&sgn(dot(p-s,p-t))<=0;
}

bool parallel(line a,line b)//Judging whether a b is parallel
{
    return !sgn(cross(a.s-a.e,b.s-b.e));
}

bool line_make_point(line a,line b,point &res)//Judging whether a line a b intersects or not, if it intersects, it returns true and stores the intersection point in res
{
    if(parallel(a,b))
        return 0;
    double s1=cross(a.s-b.s,b.e-b.s);
    double s2=cross(a.e-b.s,b.e-b.s);
    res=(s1*a.e-s2*a.s)/(s1-s2);
    return 1;
}

line move_d(line a,double len)//Translating line a along normal vector method len
{
    point d=a.e-a.s;
    d=d/d.norm();
    d.transxy(pi/2);
    return line(a.s+d*len,a.e+d*len);
}

int n;
point up[25];
point down[25];

int main()
{
    while(~scanf("%d",&n)&&n)
    {
        double ans=-1e16;
        for(int i=1;i<=n;i++)
        {
            scanf("%lf%lf",&up[i].x,&up[i].y);
            down[i].x=up[i].x,down[i].y=up[i].y-1;
        }
        bool flag=1;
        int k;
        for(int i=1;i<=n&&flag;i++)
        {
            for(int j=1;j<=n&&flag;j++)
            {
                if(j==i)
                    continue;
                for(k=1;k<=n;k++)
                    if(!seg_inter_line(line(up[i],down[j]),line(up[k],down[k])))//No intersection point
                        break;
                if(k>n)
                    flag=0;
                else if(k>max(i,j))
                {
                    point tmp;
                    if(line_make_point(line(up[i],down[j]),line(up[k-1],up[k]),tmp))
                        ans=max(ans,tmp.x);
                    if(line_make_point(line(up[i],down[j]),line(down[k-1],down[k]),tmp))
                        ans=max(ans,tmp.x);
                }
            }
        }
        if(!flag)
            printf("Through all the pipe.\n");
        else
            printf("%.2f\n",ans);
    }
    return 0;
}