1. Storage structure of binary tree

1. Sequential storage of binary trees

A set of consecutive storage units is used to store the node elements on the complete binary tree from top to bottom, and the node elements numbered I on the complete binary tree are stored in the components marked i-1 in the one-dimensional array, i.e. the zero-order storage node of the array.
Full binary tree and complete binary tree are suitable for sequential storage. The ordinal number of nodes in the tree can displace to reflect the logical relationship of node simplicity, which can not only save storage space, but also determine the location of nodes in the binary tree and the logical relationship between nodes by using the subscripts of array elements.
Example: The following binary trees are stored sequentially: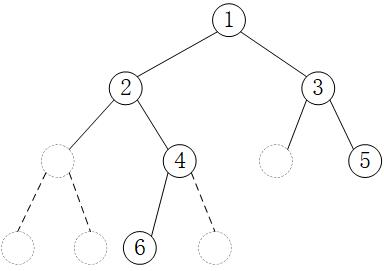
The storage results are as follows:

2. Chain Storage of Binary Trees

The schematic diagram of the chain storage structure is as follows:
Among them: lchild is used to point to the left child of the node, rchild is used to point to the right child of the node.

The structure of the chain storage structure is as follows:

tyepedef struct BiNode{
	ElemType data;
	struct BiNode *lchild;
	struct BiNode *rchild;
}BiNode,*BITree;

The chain storage schematic of the tree is shown in the following figure: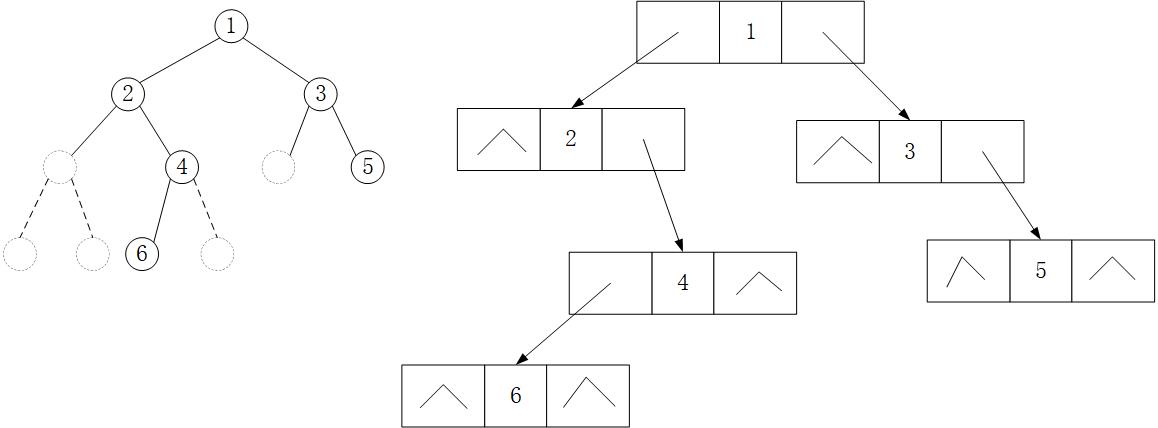

2. Traversal of Binary Trees

1. Recursive traversal of binary trees

1. Preorder traversal
Access order: root node - left subtree - right subtree

void PreOrder (BiTree T){
	if(T!=NULL){
		visit(T);  //When the code is actually running, it can be written as printf(....))
		preorder(T->lchild);  //Accessing the left subtree
		preorder(T->rchild);	//Accessing the right subtree
	}
}

2. Mid-order traversal
Access order: left subtree - root node - right subtree

void InOrder (BiTree T){
	if(T!=NULL){
		InOrder(T->lchild);
		visit(T);  //When the code is actually running, it can be written as printf(....))
		InOrder(T->rchild);
	}
}

3. Postorder traversal
Access order: left subtree - right subtree - root node

void PostOrder(BiTree T){
	if(T!=NULL){
	PostOrder(T->lchild;)
	PostOrder(T->rchild;)
	visit(T);  //When the code is actually running, it can be written as printf(....))
	}
}

2. Non-recursive traversal of binary trees

1. Priority non-recursive traversal:
Basic ideas:
1. Encounter a vertex, access it, then stack it, and traverse the left subtree.
2. After the left subtree traversal, pop up the node from the top of the stack and point to its right child. Continue step 1.
3. Stop when all the nodes are empty and the stack is empty.

void preorder2(BiTree ti){
	InitStack(s);		//Initialization stack
	Bitree t=ti;
	while(t||!IsEmpty(s)){
		while(t){
			printf("%d\n",t->data);			//access node
			push(s,t);			//Enter stack
			t=t->lchild;
		}
		if(!IsEmpty(s)){
		pop(s,t);			//Stack out
		t=t->rchild;
		}
	}
}

2. Middle-order non-recursive traversal
The path of middle-order recursive traversal is exactly the same as that of precedent traversal, and the idea is very similar to that of precedent traversal. The main difference is that the order of visiting nodes is different. The order of visiting nodes in middle-order recursive traversal is: left child-root node-right child.

void InOrder2(BiTree ti){
	InitStack(s);			//Initialization stack
	Bitree t=ti;
	while(t||!IsEmpty(s)){
		while(t){
			push(s,t);					//Enter stack
			t=t->lchild;
		}
		if(!IsEmpty(s)){
		pop(s,t);							//Stack out
		printf("%d\n",t->data);					//access node
		t=t->rchild;
		}
	}
}

3. Post-order non-recursive traversal
For a node, to achieve the order of left child-right child-root node, stack can also be used. On the premise that the node is not empty, stack the root node-right child-left child in turn, and then out of the stack can get the sequence of left child-right child-root node (i.e., the order of post-order traversal), so it can directly follow the root. Node - right child - left child traverses the whole tree in this order, then the traversal results are stacked in turn, and then unified out of the stack. We know that the traversal order of the precedence traversal is the root node - left child - right child, and the difference between the order we need is only the question of visiting the left child first or the right child, so we can refer to the structure of the precedence traversal and change the left and right order of the precedence traversal. Then we'll put the result on the stack. Next let's consider the problem. In order traversal, we print the result of visiting the node directly, but in order traversal, we need the result to be put on the stack. That is, we need to change the access mode (printf) in order traversal to press it into another stack. The code is as follows:

void postorder2(BiTree ti){
	InitStack(s1);		//s1 for storage nodes
	InitStack(s2);		//s2 for storing access results
	Bitree t=ti;
	while(t||!IsEmpty(s1)){
		while(t){
			//printf("% d n", T - > data); printf(...) in // precedent traversal, now push(s2,t);
			push(s2,t);   					//The access results are stacked in turn
			push(s1,t);  					//Place nodes on the stack in turn
			t=t->rchild;					//Access the right subtree first
		}
		if(!IsEmpty(s1)){
		pop(s1,t);
		t=t->lchild;				//Access the left subtree after accessing the right subtree
		}
	}
	
	while(!IsEmpty(s2)){				//The access results stored in s2 are sequentially stacked to get the sequence of left child-right child-root node.
		pop(s2,t);
		printf("%d\n",t->data);
	}
}

3. Hierarchical traversal of binary trees

Hierarchical traversal implementation of binary tree: now join the root node of binary tree into the queue, then leave the queue, visit the node just out of the queue, if the node has a left subtree, then put the left subtree into the stack, if the node has a right subtree, then put the right subtree into the stack; then leave the queue to the head node, then visit the node, and then judge the node. The left and right subtrees of the node are repeated until the queue is empty.
The code is as follows:

void levelorder(Bitree ti){
	Bitree t=ti;
	InitQueue(Q);		//Initialization queue
	EnQueue(t);		//Root Node Entry
	while(!IsEmpty(Q)){
		DeQueue(Q,t);	//Team Leader Element Out
		visit(t);					//Access to this node
		if(t->lchild!=NULL){			//Judging left subtree
		EnQueue(t->lchild);	
		}
		if(t->rchild!=NULL){				//Judging the Right Subtree Situation
		EnQueue(t->rchild);	
		}
	}	
}