Topic Requirements:

Given a 32-bit signed integer, you need to reverse the number on each bit of the integer.

Example 1:

Input: 123
 Output: 321

Example 2:

Input: -123
 Output: -321

Example 3:

Input: 120
 Output: 21

Example 4:

Input: 9646324351
 Output: 0

Be careful:

Assuming that our environment can only store 32-bit signed integers, the numerical range is [2's 31st power, 2's 31st power 1].

Based on this assumption, return 0 if the integer overflows after inversion.

Solution 1:

The low est method

Ideas:

Converts to a string. Get the last first and last. Used to determine whether a negative number is zero or not

Then make a judgment and deal with it according to different situations.

The following code:

public int reverse(int x) {
   String strX = Integer.valueOf(x).toString();
   char [] charArr = strX.toCharArray();
   int length = charArr.length;
   String [] strArr = new String [length];
   for(int i =0;i<length;i++){
       strArr[i] = String.valueOf(new char[]{charArr[i]});

   }
   String [] newStrArr =   new String [length];
   String fasterStr =  strArr[0];
   String lastStr = strArr[length-1];
   int index = 0;
    if("-".equals(fasterStr)
            && "0".equals(lastStr)){
        newStrArr =   new String [length-1];
        newStrArr[0] = fasterStr;
        for(int i= length-2; i >0;i--){
            index++;
            String str = strArr[i];
            newStrArr[index] = str;

        }
    }else if("0".equals(lastStr)){
       newStrArr =   new String [length-1];
       for(int i= length-2; i >=0;i--){
           String str = strArr[i];
           newStrArr[index] = str;
           index++;
       }
   }else if("-".equals(fasterStr)){
       newStrArr[0] = fasterStr;
       for(int i= length-1; i >0;i--){
           index++;
           String str = strArr[i];
           newStrArr[index] = str;
       }
   }else{
       for(int i= length-1; i >=0;i--){
           String str = strArr[i];
           newStrArr[index] = str;
           index++;
       }
   }


    String str = "";
    for(int i = 0;i<newStrArr.length;i++){
        str+= newStrArr[i];
    }
   try{
       if(""!= str && null != str){
           Integer ix = Integer.parseInt(str);
           x=ix.intValue();
       }
   }catch (Exception e){
        return 0;
   }

    return  x;
}

The results of this scheme are as follows:

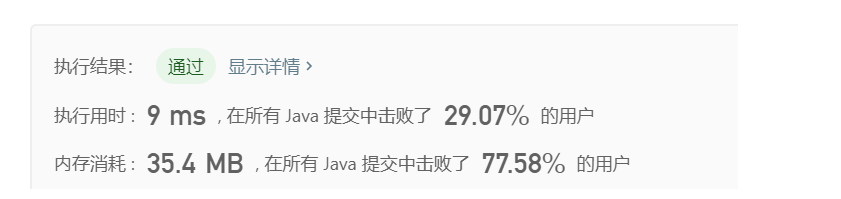
Running 9 milliseconds consumes 35.4M of memory

Solution 2:

Processing from mathematical thinking.

For example, 1234, in turn, is 4321.

That is, one-bit and one-thousand-bit exchanges, ten-bit and one-hundred-bit exchanges.

You see. That's 10 x + Y%10.

Where x is the number of digits. Y is data.

Understand the above, we can get the following code:

public int reverse2(int x) {
    //Viewed from Mathematical Thinking
    int rpc = 0;
    while (x != 0)
    {
        int newrpc = rpc*10 + x%10;
        log.info("rpc*10:{},x%10:{}，newrpc: {}",(rpc*10),x%10,newrpc);
        if ((newrpc - x%10)/10 != rpc){
            return 0;
        }
        rpc = newrpc;
        x = x/10;
    }
    log.info("==:{}",rpc);
    return rpc;
}

Print logs after running:

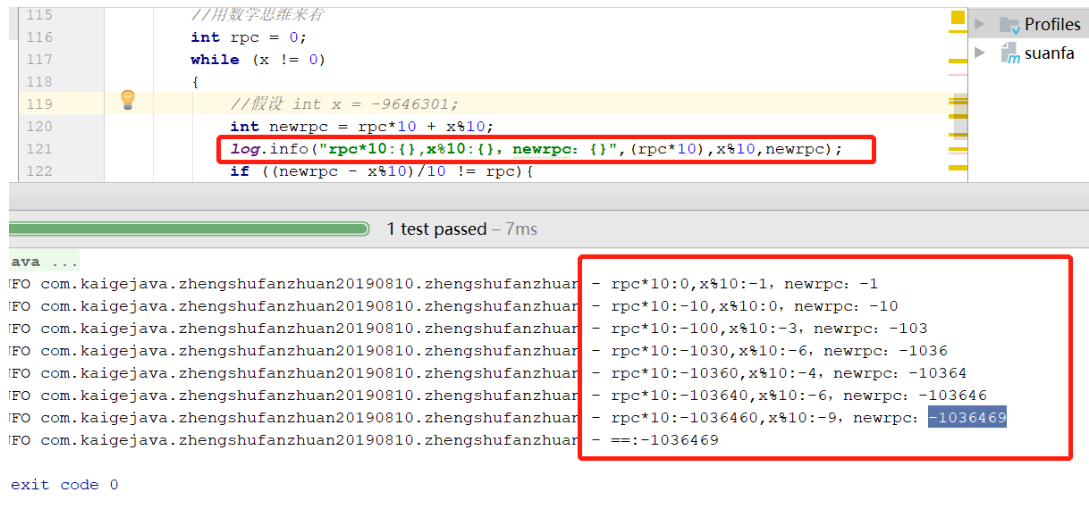
Let's take a look at the results of the implementation of this scheme:

3 milliseconds, memory consumption: 34.3M

Look at the third solution:

Idea: Use the string inversion method. When overflow occurs, the exception returns directly to 0

public int reverse3(int x) {
    try {
        if(x > 0) {
            StringBuilder str = new StringBuilder().append(x);
            return Integer.parseInt(str.reverse().toString());
        }else {
            StringBuilder str = new StringBuilder().append(-x);
            return Integer.parseInt(str.reverse().toString())*(-1);
        }
    }catch (NumberFormatException e) {
        return 0;
    }
}

The results of this scheme are as follows:

Programme 4:

Using math function, bit operation and string inversion

public int reverse4(int x){
    //Region, right endpoint
    double start =  Math.pow(2, 31) - 1;
    //Zone Left Endpoint
    double end = -Math.pow(2, 31);
    if(x<end && x>start){
        return 0;
    }
    //Get the original numeric symbol
    float df = Math.signum(x);
    Integer intDf = Math.round(df);
    //Take absolute value
    int i = Math.abs(x);
    //Inversion using sring
    StringBuilder str = new StringBuilder().append(i).reverse();
    x = Integer.parseInt(str.toString());
    log.info("==>:{}",x*intDf);
    return  x*intDf ;
}

Implementation results:

Programme V:

The displacement transport and math functions are used.

public int reverse5(int x) {
    int res = 0;
    int of = ((1 << 31) - 1) / 10;
    while (x != 0) {
        if (Math.abs(res) > ((1 << 31) - 1) / 10){
            return 0;
        }
        res = res * 10 + x % 10;
        x /= 10;
    }
    return res;
}

Implementation results:

We compare five schemes:

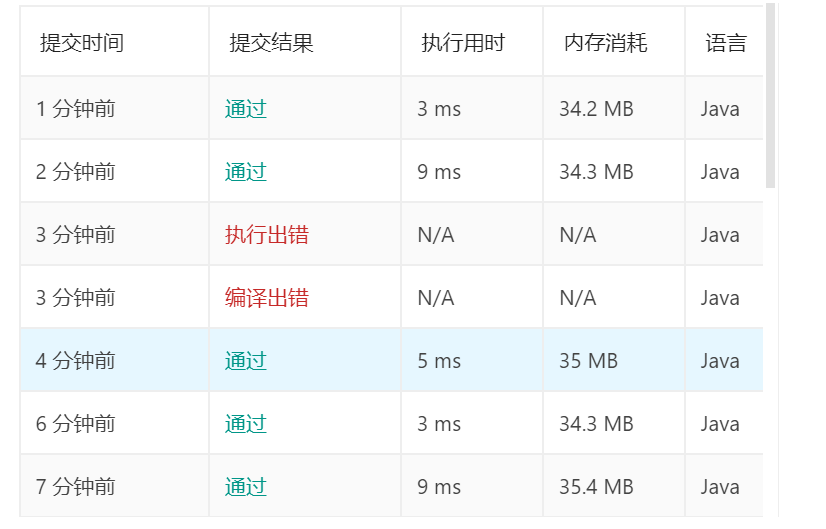
It was found that the second and fifth schemes took the shortest time. That is to say, using mathematical thinking and displacement to run fastest.

After comparing the schemes of the Five Middle Schools, do we realize that programming is an art?

Origin of this article: Kaige Java

Well, that's all for today's small algorithm. "Every day a small algorithm" hopes to be able to stick to it directly.