Try to use computers to find those wonderful and interesting numbers within a certain range, as well as the relationship between them.

Cuboid number

Definition: If the edge length x, y, Z and body diagonal length w of a cube are positive integers, they are called a set of cuboid numbers, that is, x2+y2+z2=w2.

Function: Find the cuboid array in interval [a,b] (x,y,z,w)

Violent exhaustion method: set up four cycles, four variables scan the area in turn, the symbol condition is output;

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<math.h>

int main()
{
	int a, b; //a is the lower limit and b is the upper limit.
	int x, y, z, w;
	int n=0; //Number

	printf("Input Lower Limit and Upper Limit:\n");
	scanf("%d %d", &a, &b);

	for (x = a; x <= b; x++)
	{
		for (y = x; y <= b; y++)
		{
			for (z = y; z <= b; z++)
			{
				for (w = a; w<=b ; w++) //The initial value of w here cannot be y!!
				{
					if (w*w == (z*z + y * y + x * x))
					{
						n++;
						printf("First%d Persons:%d^2+%d^2+%d^2 = %d^2\n", n,x, y, z, w);
					}
				}
			}
		}
	}
/*
	for (x = a; x <= b; x++)
	{
		for (y = x; y <= b; y++) What is the initial value of y here, not a?
		{
			for (z = y; z <= b; z++) What is the initial value of z here but not a?
			{
				......
			}
		}
	} Avoid repetitive results.
*/
	system("pause");
	return 0;
}

/*Test:
Input Lower Limit and Upper Limit:
100 200
 Number 1: 101 ^ 2 + 102 ^ 2 + 126 ^ 2 = 191 ^ 2
 Number 2: 102 ^ 2 + 102 ^ 2 + 119 ^ 2 = 187 ^ 2
 Number 3: 102 ^ 2 + 111 ^ 2 + 114 ^ 2 = 189 ^ 2
 Number 4: 102 ^ 2 + 120 ^ 2 + 120 ^ 2 = 198 ^ 2
 Fifth: 104 ^ 2 + 106 ^ 2 + 112 ^ 2 = 186 ^ 2
 Number 6: 104 ^ 2 + 107 ^ 2 + 116 ^ 2 = 189 ^ 2
 Seventh: 108 ^ 2 + 108 ^ 2 + 126 ^ 2 = 198 ^ 2
 Eighth: 108 ^ 2 + 116 ^ 2 + 117 ^ 2 = 197 ^ 2
*/

Complete Number

Definition: The sum of all positive factors less than n equals n itself.

For example: 6, the positive factors less than 6 are 1, 2, 3, and 6 = 1 + 2 + 3, then 6 is a complete number.

Find the Complete Number in the Interval [a,b] (primitive easy to understand)

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<math.h>

int main()
{
	int a, b; //a is the lower limit and b is the upper limit.
	int x, y; //Cyclic variables

	printf("Input Lower Limit and Upper Limit:\n");
	scanf("%d %d", &a, &b);

	for (x = a; x <= b; x++) //Traversing intervals [a,b], finding complete numbers
	{
		int sum = 1; //All the factors of a number have 1. Sum is the sum of the factors of a complete number.
		for (y = 2; y <= x / 2; y++) //Why divide the condition by 2? Because the greatest positive factor of a number is half of itself.
		{
			if (x%y == 0) //It's a factor of that number.
			{
				sum += y; //Summation
			}
		}

		if (sum == x) //Conditions of Complete Numbers
		{
			printf("Find the perfect number: 1");
			for (y = 2; y <= x / 2; y++)
			{
				if (x%y == 0)
				{
					printf("+%d",y);
				}
			}
			printf("=%d\n", x);
		}
	}

	system("pause");
	return 0;
}
/*Test:
Input Lower Limit and Upper Limit:
2 1000
 Find the perfect number: 1 + 2 + 3 = 6
 Find the perfect number: 1 + 2 + 4 + 7 + 14 = 28
 Find the Complete Number: 1+2+4+8+16+31+62+124+248=496
*/

Finding the Complete Number in the Interval [a,b] (Program Improvement: Optimized Trial-Discuss Algorithms)

Core Principle: The factor of a number x always appears in pairs. Except for the factor of 1 and itself, the smaller one of all the other factors must be less than or equal to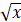 This is the case. Note that if x happens to be the square of a number, then x has only one factor, not two.

Example: 16 has a factor of 1 and 16; 2 and 8; 16 has a square of 4, at which time the factor is only one 4, not two 4.

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<math.h>

int main()
{
	int a, b; //a is the lower limit and b is the upper limit.
	int x, y; //Cyclic variables
	int t = 0;

	printf("Input Lower Limit and Upper Limit:\n");
	scanf("%d %d", &a, &b);

	for (x = a; x <= b; x++) //Traversing intervals [a,b], finding complete numbers
	{
		int sum = 1; //All the factors of a number have 1. Sum is the sum of the factors of a complete number.
		t = sqrt(x);
		for (y = 2; y <= t; y++) //The smaller of all the factors must be less than or equal to the root number x.
		{
			if (x%y == 0)
			{
				sum = sum+y+x/y; //The factor exists in pairs and finds the one less than the root number x, and the other one is x/y.
			}
		}
		if (x == t*t) //If x happens to be the square of a number, then there is only one factor of x, not two.
		{
			sum -= t;
		}

		if (sum == x) //Conditions of Complete Numbers
		{
			printf("Find the perfect number: 1");
			for (y = 2; y <= x / 2; y++)
			{
				if (x%y == 0)
				{
					printf("+%d", y);
				}
			}
			printf("=%d\n", x);
		}
	}

	system("pause");
	return 0;
}
/*Test:
Input Lower Limit and Upper Limit:
2 100000
 Find the perfect number: 1 + 2 + 3 = 6
 Find the perfect number: 1 + 2 + 4 + 7 + 14 = 28
 Find the Complete Number: 1+2+4+8+16+31+62+124+248=496
 Find the Complete Number: 1+2+4+8+16+32+64+127+254+508+1016+2032+4064=8128
*/

Narcissistic number

Definition: If a three-digit is equal to the sum of its three-digit cubes.

Core algorithms:

The number of bits of a is equal to a divided by 1 and then redundant to 10, that is, the number of bits = (a/1)%10.

The number on the ten digits of a is equal to dividing a by 10 and then finding the remainder on 10, that is, the ten digits=(a/10)%10.

The number on a hundred digits is equal to a divided by 100 and then redundant to 10, that is, 100 digits = (a/100)%10.

(1) Calculating Narcissus Number in Interval [a,b] (Programming Based on Decomposition)

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<math.h>

int main()
{
	int m,a,b,c;

	for (m = 100; m <= 999; m++) //The major premise of the number of daffodils is only three digits.
	{
		a = m % 10; //Personality
		b = (m / 10) % 10;
		c = (m / 100) % 10; //Hundred
		if (m == (a*a*a + b * b*b + c * c*c))
		{
			printf("%d It's the number of daffodils\n",m);
		}
	}

	system("pause");
	return 0;
}
/*Output:
153 It's the number of daffodils
370 It's the number of daffodils
371 It's the number of daffodils
407 It's the number of daffodils
*/

(2) Calculating Narcissus Number in Interval [a,b] (Programming Based on Combination)

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<math.h>

int main()
{
	int m,a,b,c;

	for (a = 1; a <= 9; a++) //a is 100
	{
		for (b = 0; b <= 9; b++) //b is ten
		{
			for (c = 0; c <= 9; c++)
			{
				m = a * 100 + b * 10 + c;
				if (m == (a*a*a + b * b*b + c * c*c))
				{
					printf("%d It's the number of daffodils\n", m);
				}
			}
		}
	}
	system("pause");
	return 0;
}
/*Output:
153 It's the number of daffodils
370 It's the number of daffodils
371 It's the number of daffodils
407 It's the number of daffodils
*/

Randall number

Definition: An n (n >= 3) bit positive integer equals the sum of the N powers of its N digits

Randle number is also called self-power, three Randle number is also called Narcissus number, four is called Rose number, five is called pentagonal star number, six is called hexagonal number.

Find the Randall number of n(3<=n<=9):

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<math.h>

int main()
{
	int n,i; //n is a digit and j is a cyclic variable
	double a, t,sum,k,x;

	printf("Please enter digits n(2<n<10):\n");
	scanf("%d", &n);

	t = 1;
	for (i = 1; i <= n - 1; i++)
	{
		t *= 10;
	}
	for (a = t + 1; a <= t * 10 - 1; a++) //Ergodic n-bit integers
	{
		x = a;
		for (sum = 0, i = 1; i <= n; i++) //n arrays of circularly separated integer a
		{
			k = fmod(x, 10); //Remainder
			sum += pow(k, n); //power
			x = floor(x / 10);
		}
		if (sum == a)
		{
			printf("Find one:%.0lf\n", a);
		}
	}

	system("pause");
	return 0;
}
/*Test:
Please enter the digit n (2 < n < 10):
7
 Find one: 1741725
 Find one: 4210818
 Find one: 9800817
 Find one: 9926315
*/

 

Conservative number

Also known as isomorphic number, definition: positive integer n is the tail of its square, then n is called conservative number.

Example: 6 is the tail of its square 36, 6 is the conservative number; 76 is the tail of its square 5776, 76 is the conservative number.

 

Find all conservative numbers in interval [a,b]

Algorithm:

1. The square of the calculated number n is s.

2. Calculate the number of digits len of n, let t=10^len, then the tail number p=s%t of n;

3. The establishment condition is n==p.

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>

int main()
{
	int a, b;
	int n; //Cyclic variables
	int s,len,k,p; //The square of the number N in the interval; len denotes the number of digits of n; p is the tail of n.

	printf("Input interval[a,b]:\n");
	scanf("%d %d", &a, &b);

	for (n = a; n <= b; n++)
	{
		s = n * n;
		len = 1;
		k =n; //The function of the k variable is to find the number of digits of s.
		while (k > 0)
		{
			len *= 10;
			k /= 10;
		}
		p = s % len; //Tail
		if (n == p)
		{
			printf("%d The square equals%d, %d Is a conservative number\n", n, s, n);
		}
	}
	system("pause");
	return 0;
}
/*Test:
Input interval [a,b]:
10 100000
25 The square equals 625, and 25 is a conservative number.
76 The square equals 5776, 76 is a conservative number.
376 The square is 141376, 376 is conservative.
625 The square equals 390625, 625 is a conservative number
9376 The square equals 87909376, 9376 is a conservative number.
*/