Machine Learning (Zhou Zhihua) Watermelon Book Chapter 7 Exercise 7.3-Python Implementation

• Experimental topics

Laplacian modified naive Bayesian classifier is implemented by trial programming. The watermelon data set 3.0A is used as training set to discriminate P.151 "test 1" samples.

• Experimental principle

Laplacian correction avoids the problem that the probability estimate is zero due to insufficient training set samples.

Naive Bayesian classifier:

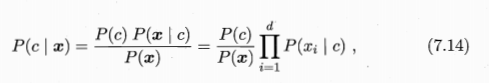
Naive Bayesian Classifier Expressions

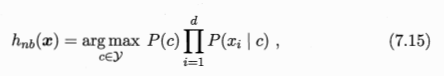
Laplace's revised prior-like probability formula

Laplacian modified conditional probability formula for discrete attributes

Conditional probability formula for continuous attributes

• Experimental process

Data Set Acquisition

Get the watermelon data set 3.0A in the book and coexist as data_3 a.txt

Density, sugar content, melon
 0.6970000000000001, 0.46, yes
 0.774, 0.376, yes
 0.634, 0.264, yes
 0.608, 0.318, yes
 0.556, 0.215, yes
 0.4029999999999999997, 0.237, yes
 0.48100000000004,0.149,
0.43700000000006,0.21100000000000002
 0.665999999999999999, 0.091, no
 0.243, 0.267, no
 0.245, 0.057, no
 0.3429999999999999997, 0.099, no
 0.639, 0.161, no
 0.657, 0.198, no
 0.36, 0.37, no
 0.593, 0.042, no
 0.7190000000000001, 0.10300000000000001, no

Algorithm implementation

Data Definition, Defining Attributes and Their Value Categories, Class Label Categories

Read data function

Generating prediction data

Generate a set of samples of different label classes by label class

Computing Class Prior Probability

Computing Conditional Probability of Discrete Attributes

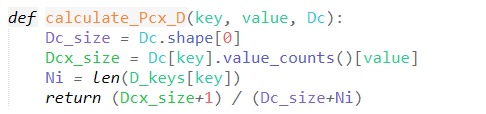
Computing Conditional Probability of Continuous Attributes

Calculate the probabilistic reliability of determining the test sample as label

Predictive test sample labeling

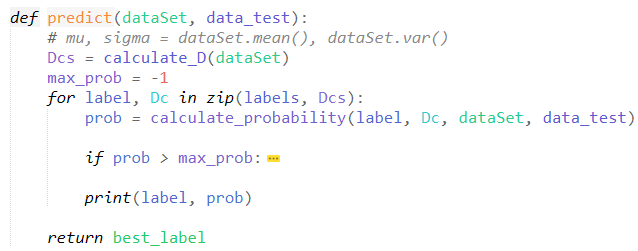
main function, calling the above function

• experimental result

• List of procedures:

import math
import numpy as np
import pandas as pd

D_keys = {
	'Color and lustre': ['Dark green', 'Jet black', 'plain'], 
	'Pedicle': ['Curl up', 'Stiff', 'Curl up'], 
	'stroke': ['Crisp and crisp', 'Dreary', 'Voiced sound'], 
	'texture': ['Slightly paste', 'vague', 'clear'], 
	'Umbilicus': ['Sunken', 'Slightly concave', 'flat'], 
	'Touch': ['Soft sticky', 'Hard slip'], 
}
Class, labels = 'Good melon', ['yes', 'no']

# Read data
def loadData(filename):
	dataSet = pd.read_csv(filename)
	dataSet.drop(columns=['number'], inplace=True)
	return dataSet

# Configuration Test 1 Data
def load_data_test():
	array = ['Dark green', 'Curl up', 'Voiced sound', 'clear', 'Sunken', 'Hard slip', 0.697, 0.460, '']
	dic = {a: b for a, b in zip(dataSet.columns, array)}
	return dic

def calculate_D(dataSet):
	D = []
	for label in labels:
		temp = dataSet.loc[dataSet[Class]==label]
		D.append(temp)

	return D

def calculate_Pc(Dc, D):
	D_size = D.shape[0]
	Dc_size = Dc.shape[0]
	N = len(labels)
	return (Dc_size+1) / (D_size+N)

def calculate_Pcx_D(key, value, Dc):
	Dc_size = Dc.shape[0]
	Dcx_size = Dc[key].value_counts()[value]
	Ni = len(D_keys[key])
	return (Dcx_size+1) / (Dc_size+Ni)

def calculate_Pcx_C(key, value, Dc):
	mean, var = Dc[key].mean(), Dc[key].var()
	exponent = math.exp(-(math.pow(value-mean, 2) / (2*var)))
	return (1 / (math.sqrt(2*math.pi*var)) * exponent)

def calculate_probability(label, Dc, dataSet, data_test):
	prob = calculate_Pc(Dc, dataSet)
	for key in Dc.columns[:-1]:
		value = data_test[key]
		if key in D_keys:
			prob *= calculate_Pcx_D(key, value, Dc)
		else:
			prob *= calculate_Pcx_C(key, value, Dc)

	return prob

def predict(dataSet, data_test):
	# mu, sigma = dataSet.mean(), dataSet.var()
	Dcs = calculate_D(dataSet)
	max_prob = -1
	for label, Dc in zip(labels, Dcs):
		prob = calculate_probability(label, Dc, dataSet, data_test)

		if prob > max_prob:
			best_label = label
			max_prob = prob

		print(label, prob)

	return best_label


if __name__ == '__main__':
	# Read data
	filename = 'data_3.txt'
	dataSet = loadData(filename)
	data_test = load_data_test()
	label = predict(dataSet, data_test)
	print('Forecast results:', label)