I. Basic concepts

Each node has at most two subtrees, the left subtree and the right subtree, the order can not be reversed.

Nature:

1. There are at most 2^(n-1) elements on the n-th layer of a non-empty binary tree.

2. Binary trees with depth of h have at most 2^h-1 nodes.

Full Binary Tree: All terminals are at the same level, and the degree of non-terminal nodes is 2.

If the depth of a full binary tree is h, the number of nodes it contains must be 2^h-1.

Complete binary tree: Except for the largest level, which is a full binary tree and the largest level, all the nodes are aligned to the left, that is, they are concentrated on the left, and can not have an empty position.

For a complete binary tree, if a node is i, its parent node is i/2, 2I is left child and 2i+1 is right child.

II. Storage structure

Sequential storage:

take data structure There is a fixed array.

1. #define LENGTH 100  
2. typedef char datatype;  
3. typedef struct node{  
4.     datatype data;  
5.     int lchild,rchild;  
6.     int parent;  
7. }Node;  
8.   
9. Node tree[LENGTH];  
10. int length;  
11. int root;  

Although it has some advantages in traversal speed, it is a non-mainstream binary tree because of its large space. Binary trees are usually stored in chains.

Chain storage:

1. typedef char datatype;  
2.   
3. typedef struct BinNode{  
4.     datatype data;  
5.     struct BinNode* lchild;  
6.     struct BinNode* rchild;  
7. }BinNode;  
8.   
9. typedef BinNode* bintree;          //bintree itself is a pointer to a node  

Traversal of Binary Trees

Traverse all nodes of the upcoming tree and visit only once. According to the location of root node, it can be divided into pre-order traversal, middle-order traversal and post-order traversal.

Preorder traversal: root node - > left subtree - > right subtree

Mid-order traversal: left subtree - > root node - > right subtree

Postorder traversal: left subtree - > right subtree - > root node

For example, find three traversals of the following tree

 

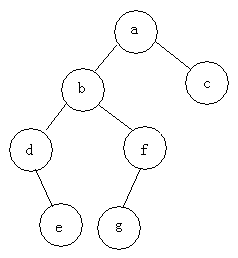
Preorder traversal: abdefgc

Intermediate traversal: debgfac

Post-order traversal: edgfbca

4. Realization of traversal

Recursive implementation (previous sequential traversal, for example, except for slightly different output locations)

1. void preorder(bintree t){  
2.     if(t){  
3.         printf("%c ",t->data);  
4.         preorder(t->lchild);  
5.         preorder(t->rchild);  
6.     }  
7. }  

Non-recursive Implementation

Because you have to come back after traversing the root node, you have to save it. Considering the characteristics of LIFO, stack storage is selected. The number is determined and stored on a sequential stack.

1. #define SIZE 100  
2. typedef struct seqstack{  
3.     bintree data[SIZE];  
4.     int tag[SIZE];   //Prepared for subsequent Traversals  
5.     int top;     //top is the subscript of an array  
6. }seqstack;  
7.   
8. void push(seqstack *s,bintree t){  
9.   
10.     if(s->top == SIZE){  
11.         printf("the stack is full\n");  
12.     }else{  
13.         s->top++;  
14.         s->data[s->top]=t;  
15.     }  
16. }  
17.   
18. bintree pop(seqstack *s){  
19.     if(s->top == -1){  
20.         return NULL;  
21.     }else{  
22.         s->top–;  
23.         return s->data[s->top+1];  
24.     }  
25. }  

1. Preorder traversal

1. void preorder_dev(bintree t){  
2.     seqstack s;  
3.     s.top = -1;     //Because top here represents the position in the array, null is -1  
4.     if(!t){  
5.         printf("the tree is empty\n");  
6.     }else{  
7.         while(t || s.stop != -1){  
8.             while(t){    //As long as the node is not empty, it should be stored on the stack, regardless of its left and right nodes.  
9.                   printf("%c ",t->data);  
10.                 push(&s,t);  
11.                 t= t->lchild;  
12.             }  
13.             t=pop(&s);  
14.             t=t->rchild;  
15.         }  
16.     }  
17. }  

2. Mid-order traversal

 

1. void midorder(bintree t){  
2.     seqstack s;  
3.     s.top = -1;  
4.     if(!t){  
5.         printf("the tree is empty!\n");  
6.     }else{  
7.         while(t ||s.top != -1){  
8.             while(t){  
9.                 push(&s,t);  
10.                 t= t->lchild;  
11.             }  
12.             t=pop(&s);  
13.             printf("%c ",t->data);  
14.             t=t->rchild;  
15.         }  
16.     }  
17. }  

 

3. Postorder traversal

Because the last step of post-order traversal is to visit the root node once, it is necessary to visit the root node twice. To solve this problem, the method of pinching mark position is adopted.

This code is very tangled, and friends who have confidence in themselves can try to write it independently. Anyway, I've been writing for a long time. Logic is not difficult. I drew a logic diagram.

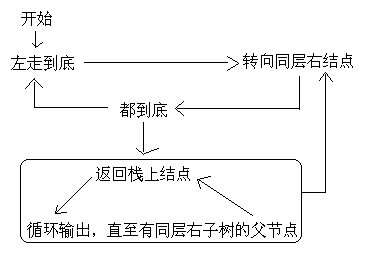
Code:

 

1. void postorder_dev(bintree t){  
2.     seqstack s;  
3.     s.top = -1;  
4.     if(!t){  
5.         printf("the tree is empty!\n");  
6.     }else{  
7.         while(t || s.top != -1){    //The stack is empty and t is empty.  
8.             while(t){  
9.                 push(&s,t);  
10.                 s.tag[s.top] = 0;   //Set the access tag, 0 for the first access and 1 for the second access.  
11.                 t= t->lchild;  
12.             }  
13.             if(s.tag[s.top] == 0){  //On the first visit, turn to the right node at the same level  
14.                 t= s.data[s.top];   //t is empty when left comes to the end. It must be so!  
15.                 s.tag[s.top]=1;       
16.                 t=t->rchild;  
17.             }else {  
18.                 while (s.tag[s.top] == 1){ //Find the next first accessed node in the stack and exit the loop without pop so it is its left child node  
19.                     t = pop(&s);  
20.                     printf("%c ",t->data);  
21.                 }  
22.                 t = NULL; //t must be empty. Skip left and go right.  
23.             }  
24.         }  
25.     }  
26. }  

4. Hierarchical traversal: that is, each layer output from left to right

Elements need to be stored first in first out, so queue storage is chosen.

The definition of queue:

1. #define MAX 1000  
2.   
3. typedef struct seqqueue{  
4.     bintree data[MAX];  
5.     int front;  
6.     int rear;  
7. }seqqueue;  
8.   
9.   
10. void enter(seqqueue *q,bintree t){  
11.     if(q->rear == MAX){  
12.         printf("the queue is full!\n");  
13.     }else{  
14.         q->data[q->rear] = t;  
15.         q->rear++;  
16.     }  
17. }  
18.   
19. bintree del(seqqueue *q){  
20.     if(q->front == q->rear){  
21.         return NULL;  
22.     }else{  
23.         q->front++;  
24.         return q->data[q->front-1];  
25.     }  
26. }  

Traversal implementation

1. void level_tree(bintree t){  
2.     seqqueue q;  
3.     bintree temp;  
4.     q.front = q.rear = 0;  
5.     if(!t){  
6.         printf("the tree is empty\n");  
7.         return ;  
8.     }  
9.     enter(&q,t);  
10.     while(q.front != q.rear){  
11.         t=del(&q);  
12.         printf("%c ",t->data);  
13.         if(t->lchild){  
14.             enter(&q,t->lchild);  
15.         }  
16.         if(t->rchild){  
17.             enter(&q,t->rchild);  
18.         }  
19.     }  
20. }  

 

5. Generating Binary Trees from the Results of Preorder Traverse

1. //Recursive calls, no points, only focus on one point when thinking, because it will come back, do not track the operation of the program, otherwise it is easy to add more loops.  
2.   
3. void createtree(bintree *t){        
4.     datatype c;  
5.     if((c=getchar()) == '#')  
6.         *t = NULL;  
7.     else{  
8.         *t = (bintree)malloc(sizeof(BinNode));  
9.         (*t)->data = c;  
10.         createtree(&(*t)->lchild);  
11.         createtree(&(*t)->rchild);  
12.     }  
13. }  

6. Binary Tree Search

1. bintree search_tree(bintree t,datatype x){  
2.     if(!t){  
3.         return NULL;  
4.     }  
5.     if(t->data == x){  
6.         return t;  
7.     }else{  
8.         if(!search_tree(t->lchild,x)){  
9.             return search_tree(t->rchild,x);  
10.         }  
11.         return t;  
12.     }  
13. }  

7. Number of Statistical Nodes

1. int count_tree(bintree t){  
2.     if(t){  
3.         return (count_tree(t->lchild)+count_tree(t->rchild)+1);  
4.     }  
5.     return 0;  
6. }  

int count_tree(bintree t){
    if(t){
        return (count_tree(t->lchild)+count_tree(t->rchild)+1);
    }
    return 0;
}

8. Compare the two trees

1. int is_equal(bintree t1,bintree t2){  
2.     if(!t1 && !t2){      //All empty is equal.  
3.         return 1;  
4.     }  
5.     if(t1 && t2 && t1->data == t2->data){      //If one is empty or the data is different, it will not be judged.  
6.         if(is_equal(t1->lchild,t2->lchild))  
7.             if(is_equal(t1->rchild,t2->rchild)){  
8.                 return 1;  
9.             }  
10.     }  
11.     return 0;  
12. }  

9. Finding the Depth of Binary Trees

1. int hight_tree(bintree t){  
2.     int h,left,right;  
3.     if(!t){  
4.         return 0;  
5.     }  
6.     left = hight_tree(t->lchild);  
7.     right = hight_tree(t->rchild);  
8.     h = (left>right?left:right)+1;  
9.     return h;  
10. }  

int hight_tree(bintree t){
    int h,left,right;
    if(!t){
        return 0;
    }
    left = hight_tree(t->lchild);
    right = hight_tree(t->rchild);
    h = (left>right?left:right)+1;
    return h;
}