subject

As shown in the figure: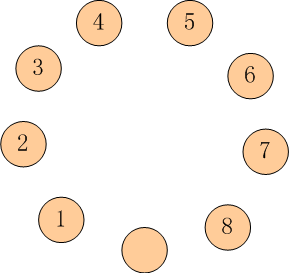

There are nine plates in a circle.
Eight of the plates contained eight grasshoppers and one was empty.
We numbered these grasshoppers clockwise 1 to 8.

Each grasshopper can jump into an adjacent empty dish.
You can also jump over an adjacent grasshopper into an empty dish with a little more force.

Please calculate if you want the grasshoppers to be arranged counter-clockwise.
And keep the position of the empty disk unchanged (i.e. 1-8, 2-7, etc.) How many jumps will it take at least?

Note: The required submission is an integer, please do not fill in any superfluous content or explanatory text.

Code

#include <iostream>
#include <queue>
#include <set>

using namespace std;
char *start = "012345678";
char *target = "087654321";

struct StateAndLevel {
    char *state;
    int level;
    int pos0;

    StateAndLevel(char *_state, int _level, int _pos0) : state(_state), level(_level), pos0(_pos0) {}
};

struct cmp {
    bool operator()(char *a, char *b) {
        return strcmp(a, b) < 0;
    }
};

queue<StateAndLevel> q;
set<char *, cmp> allState;

void swap(char *s, int a, int b) {
    char t = s[a];
    s[a] = s[b];
    s[b] = t;
}

void addNei(char *state, int pos, int newPos, int le) {
    char *new_state = (char *) malloc(9 * sizeof(char));
    strcpy(new_state, state);
    //exchange
    swap(new_state, pos, newPos);
    if (allState.find(new_state) == allState.end()) {
        allState.insert(new_state);
        q.push(StateAndLevel(new_state, le + 1, newPos));
    }
}

int main(int argc, const char *argv[]) {
    q.push(StateAndLevel(start, 0, 0));
    allState.insert(start);

    while (!q.empty()) {
        StateAndLevel sal = q.front();
        char *state = sal.state;
        int le = sal.level;
        if (strcmp(state, target) == 0) {//The current state of evolution is already the target state.
            cout << le << endl;
            return 0;
        }
        int pos0 = sal.pos0;

        int new_pos = (pos0 - 1 + 9) % 9;
        addNei(state, pos0, new_pos, le);
        new_pos = (pos0 - 2 + 9) % 9;
        addNei(state, pos0, new_pos, le);
        new_pos = (pos0 + 1 + 9) % 9;
        addNei(state, pos0, new_pos, le);
        new_pos = (pos0 + 2 + 9) % 9;
        addNei(state, pos0, new_pos, le);
        q.pop();
    }
    return 0;
}