Gray Histogram Source Code
The essence of gray histogram is to count the probability of gray occurrence of each pixel in an image.
Abscissa: 0-255 ordinate probability p (0-1)
# 10-2552 probability import cv2 import numpy as np import matplotlib.pyplot as plt %matplotlib inline img = cv2.imread('image0.jpg',1) imgInfo = img.shape height = imgInfo[0] width = imgInfo[1] # Grayscale gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) # count records the probability of each gray value appearing count = np.zeros(256,np.float) # for loop traverses every point in the picture for i in range(0,height): for j in range(0,width): # Get the gray value of the current picture pixel = gray[i,j] # Convert to int type index = int(pixel) # Let's take this gray scale factor, like count's 255 element, which was originally zero now + 1 count[index] = count[index]+1 # The gray level is counted and the probability of occurrence is calculated. for i in range(0,255): count[i] = count[i]/(height*width) # Drawing Method Using Matplotlib # Number of 0-255: 256 x = np.linspace(0,255,256) y = count plt.bar(x,y,0.8,alpha=1,color='b') plt.show() cv2.waitKey(0)
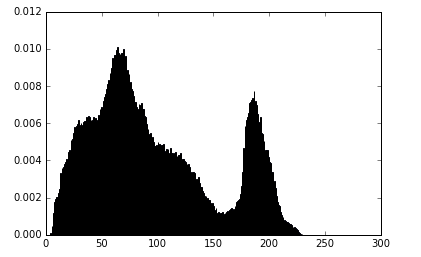
mark
Using Inline to display the color in the browser is incorrect. And delete this line is blue.
Color Histogram Source Code
# Essence: Statistical probability of gray level occurrence for each pixel is 0-255 p # For color histogram, three channels are counted separately. import cv2 import numpy as np import matplotlib.pyplot as plt %matplotlib inline img = cv2.imread('image0.jpg',1) imgInfo = img.shape height = imgInfo[0] width = imgInfo[1] # b-channel probability count_b = np.zeros(256,np.float) count_g = np.zeros(256,np.float) count_r = np.zeros(256,np.float) # for loop traverses every point for i in range(0,height): for j in range(0,width): (b,g,r) = img[i,j] index_b = int(b) index_g = int(g) index_r = int(r) count_b[index_b] = count_b[index_b]+1 count_g[index_g] = count_g[index_g]+1 count_r[index_r] = count_r[index_r]+1 # Computing probability for i in range(0,256): count_b[i] = count_b[i]/(height*width) count_g[i] = count_g[i]/(height*width) count_r[i] = count_r[i]/(height*width) # Drawing lines, x-axis coordinates x = np.linspace(0,255,256) plt.figure(12) y1 = count_b plt.subplot(221) plt.bar(x,y1,0.9,alpha=1,color='b') y2 = count_g plt.subplot(222) plt.bar(x,y2,0.9,alpha=1,color='g') y3 = count_r plt.subplot(223) plt.bar(x,y3,0.9,alpha=1,color='r') plt.show() cv2.waitKey(0)
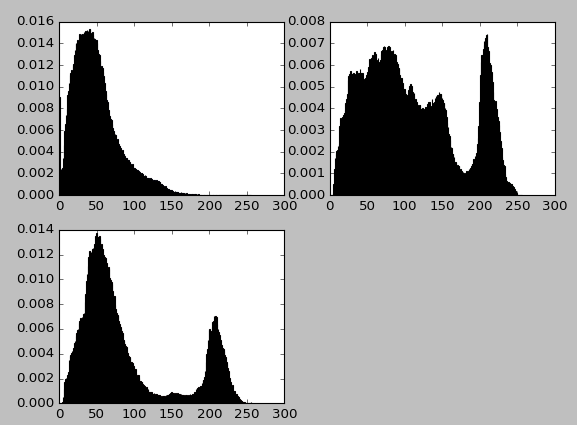
mark
I don't know why the color is wrong.
histogram equalization
# Essence of Histogram: Statistical probability of occurrence of gray level of each pixel is 0-255 p(0-1) # Histogram equalization means: # The concept of cumulative probability # The occurrence probability of the first gray level is 0.2 and the cumulative probability is 0.2. # The second gray level occurrence probability is 0.3 cumulative probability 0.5 (0.2 + 0.3) # The third gray level occurrence probability is 0.1 cumulative probability 0.6 (0.5 + 0.1) # 256 gray levels, each gray level will have a probability and a cumulative probability # 100 This gray level has a cumulative probability of 0.5,255*0.5=the value of new # You can get a mapping of 100 to a new value # After that, all gray levels of 100 are replaced by 255*0.5. # This process is called histogram equalization. import cv2 import numpy as np import matplotlib.pyplot as plt img = cv2.imread('image0.jpg',1) imgInfo = img.shape height = imgInfo[0] width = imgInfo[1] # Grayscale gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) cv2.imshow('src',gray) count = np.zeros(256,np.float) for i in range(0,height): for j in range(0,width): pixel = gray[i,j] index = int(pixel) count[index] = count[index]+1 # Calculating single probability of gray level for i in range(0,255): count[i] = count[i]/(height*width) #Calculating cumulative probability sum1 = float(0) for i in range(0,256): sum1 = sum1+count[i] count[i] = sum1 # At this point count stores the cumulative probability corresponding to each gray level. # print(count) # Compute the mapping table data type to unit16 map1 = np.zeros(256,np.uint16) for i in range(0,256): # Because the count value at this time is the cumulative probability, multiply 255 as the real mapping value. map1[i] = np.uint16(count[i]*255) # Completion mapping for i in range(0,height): for j in range(0,width): pixel = gray[i,j] # The subscript of the mapping table is obtained from the current gray value to the mapping value. gray[i,j] = map1[pixel] cv2.imshow('dst',gray) cv2.waitKey(0)
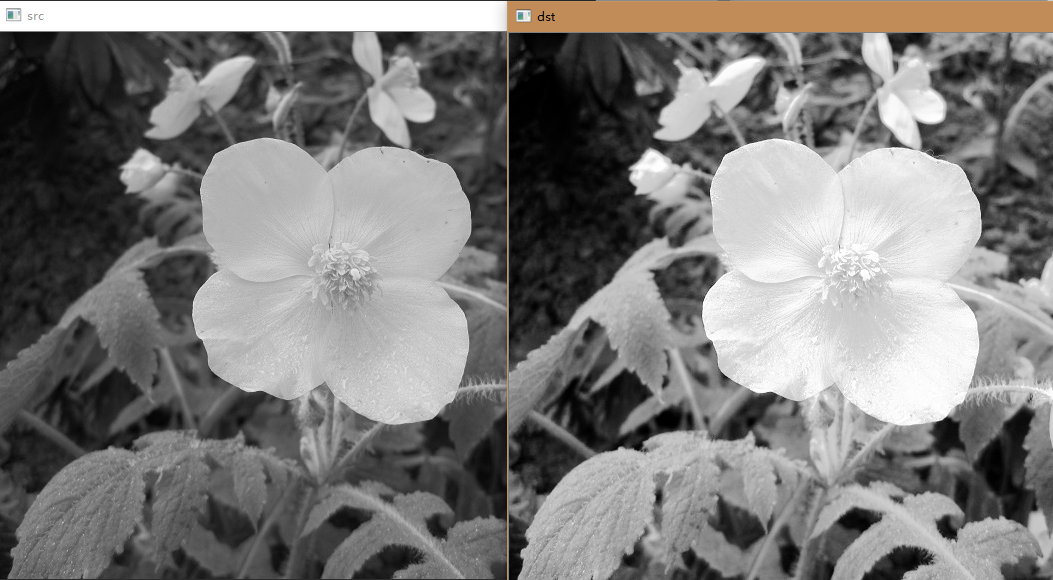
mark
Color histogram equalization
# Essence: Statistical probability of gray level occurrence for each pixel is 0-255 p # Cumulative probability # 1 0.2 0.2 # 2 0.3 0.5 # 3 0.1 0.6 # 256 # 100 0.5 255*0.5 = new # 1 Statistical probability of each color 2 Cumulative probability 1 30-255 255*p # 4 pixel import cv2 import numpy as np import matplotlib.pyplot as plt img = cv2.imread('image0.jpg',1) cv2.imshow('src',img) imgInfo = img.shape height = imgInfo[0] width = imgInfo[1] # Three count s, describing the probability of color occurrence, respectively count_b = np.zeros(256,np.float) count_g = np.zeros(256,np.float) count_r = np.zeros(256,np.float) # Get the number of color values corresponding to all the pixels for i in range(0,height): for j in range(0,width): (b,g,r) = img[i,j] index_b = int(b) index_g = int(g) index_r = int(r) count_b[index_b] = count_b[index_b]+1 count_g[index_g] = count_g[index_g]+1 count_r[index_r] = count_r[index_r]+1 # Calculate the probability of each occurrence for i in range(0,255): count_b[i] = count_b[i]/(height*width) count_g[i] = count_g[i]/(height*width) count_r[i] = count_r[i]/(height*width) # Calculating cumulative probability sum_b = float(0) sum_g = float(0) sum_r = float(0) for i in range(0,256): sum_b = sum_b+count_b[i] sum_g = sum_g+count_g[i] sum_r = sum_r+count_r[i] count_b[i] = sum_b count_g[i] = sum_g count_r[i] = sum_r #print(count) # Computing three mapping tables map_b = np.zeros(256,np.uint16) map_g = np.zeros(256,np.uint16) map_r = np.zeros(256,np.uint16) # Create three mapping tables for i in range(0,256): map_b[i] = np.uint16(count_b[i]*255) map_g[i] = np.uint16(count_g[i]*255) map_r[i] = np.uint16(count_r[i]*255) # mapping # Final data dst = np.zeros((height,width,3),np.uint8) # Read each point and map it for i in range(0,height): for j in range(0,width): (b,g,r) = img[i,j] b = map_b[b] g = map_g[g] r = map_r[r] # Target Picture Data Filling dst[i,j] = (b,g,r) cv2.imshow('dst',dst) cv2.waitKey(0)

mark
Brightness enhancement
Formula:
p = p + 40
Brightness enhancement is accomplished after simple addition.
# p = p + 40 import cv2 import numpy as np img = cv2.imread('image0.jpg',1) imgInfo = img.shape height = imgInfo[0] width = imgInfo[1] cv2.imshow('src',img) # The final image data we generated dst = np.zeros((height,width,3),np.uint8) # Traverse through each point in the picture for i in range(0,height): for j in range(0,width): # Take out three channels at each point (b,g,r) = img[i,j] bb = int(b)+40 gg = int(g)+40 rr = int(r)+40 # Judgment does not go beyond boundaries if bb>255: bb = 255 if gg>255: gg = 255 if rr>255: rr = 255 # Data Fill in Target Picture dst[i,j] = (bb,gg,rr) cv2.imshow('dst',dst) cv2.waitKey(0)

mark
The brightness of the picture did increase, but it seemed to be covered with a white mask.