Portal

Analysis

Ray method

Although this ray method has many special cases to be judged, it is still quite useful in general.

To judge the relationship between a point and a polygon, if the ray method is used, that is, to make a ray parallel to the x-axis from this point to the right and see how many times it intersects the polygon.

If it intersects even times, it will not be inside the polygon (equivalent to passing through the polygon, not remaining inside).

If an odd number of intersections occur, then the polygon is inside.

1. Give special consideration to this situation.

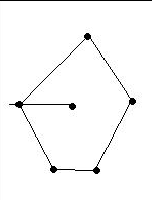
If it happens to pass through a point, it will be calculated twice according to our method (the upper edge once, the lower edge once), which is obviously wrong.

So we have to make it compulsory to go through the left (or right) endpoint on one side before it can be calculated.

2. If this point falls right on the edge of the polygon, we need to judge it.

3. Since the ray method extends in one direction, when one side is added and the other side is turned to the left (or right) side of the point, the counting cannot be included.

This is how it is implemented in code:
 

int d1=a[i].y-b.y;int d2=a[j].y-b.y;
if((det>=0&&d1<0&&d2>=0)||(det<=0&&d1>=0&&d2<0)) cnt++;

d1 records the difference between the vertex of i and the ordinate of b, and d2 records the difference between the vertex of i+1 and the ordinate of B.

Code

#include<bits/stdc++.h>
using namespace std;
const double eps=1e-7;
struct point{
	int x,y;
	point (int _x=0.0,int _y=0.0):x(_x),y(_y){} 
	friend inline point operator +(const point &a,const point &b){
		return point(a.x+b.x,a.y+b.y);
	}
	friend inline point operator -(const point &a,const point &b){
		return point(a.x-b.x,a.y-b.y);
	}
	friend inline point operator *(double k,const point &a){
		return point(k*a.x,k*a.y);
	}
	friend inline int dot(const point &a,const point &b){
		return (a.x*b.x+a.y*b.y);
	}
	friend inline int cross(const point &a,const point &b){
		return (a.x*b.y-b.x*a.y);
	}
	friend inline double len(const point &a){
		return sqrt(dot(a,a));
	}
	friend inline double dis (const point &a,const point &b){
		return len(a-b);
	}//Common Operations of Vectors 
}a[105],b;
int n,m;
bool check(){
	int cnt=0;
	for(int i=1;i<=n;++i){
		int j=i+1;
		if(j>n) j=1;
		int det=cross(a[i]-b,a[j]-b);
		if(det==0)	if(dot(a[i]-b,a[j]-b)<=0) return 1;
		int d1=a[i].y-b.y;int d2=a[j].y-b.y;
		if((det>=0&&d1<0&&d2>=0)||(det<=0&&d1>=0&&d2<0)) cnt++;
	}
	return cnt&1;
}
int main(){
	for(int tt=1;;tt++){
		scanf("%d",&n);
		if(n==0) break;
		scanf("%d",&m);
		int i,j,k;
		for(i=1;i<=n;++i)
			scanf("%d%d",&a[i].x,&a[i].y);
		if(tt!=1) printf("\n");
		printf("Problem %d:\n",tt);	
		for(i=1;i<=m;++i){
			scanf("%d%d",&b.x,&b.y);
			if(check()) printf("Within\n");
			else printf("Outside\n");
		}
	} 
	return 0;
}