Single linked list reverse order (in situ reverse)

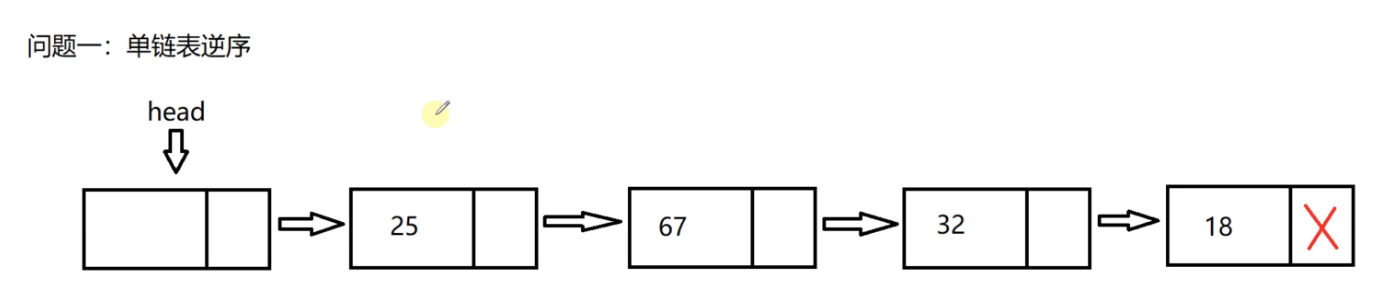
The result of the reverse order of the single linked list is that when we access the header node of the single linked list, the order of the accessed nodes is: 18, 32, 67, 25

Data structure and algorithm are always inseparable from the concept of complexity

The time consumed by algorithm execution and the memory space occupied by algorithm execution
The smaller the complexity, the better, which means that the higher the performance, the smaller the memory space and the faster the processing speed.

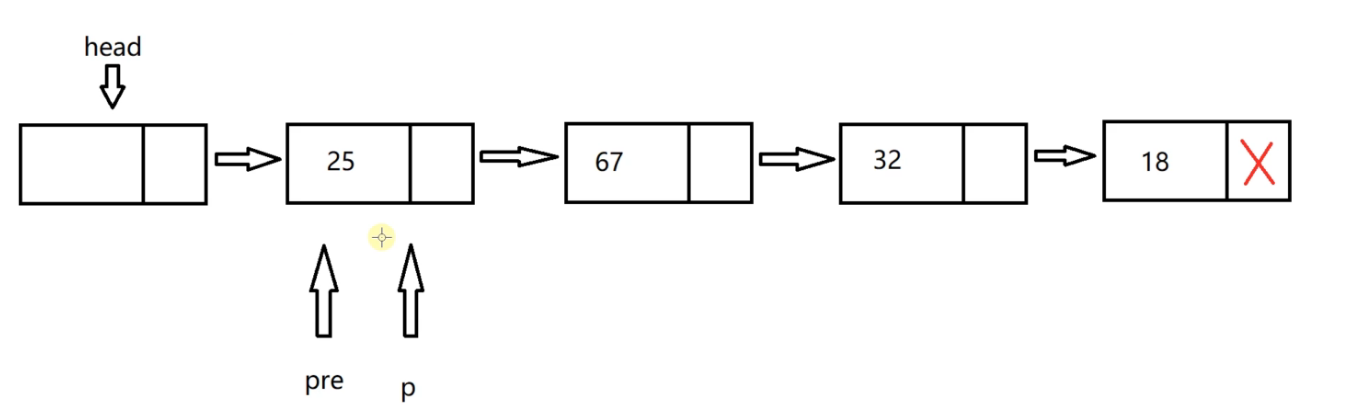
We should think: the linked list inserted by the head insertion method is just the opposite of the input
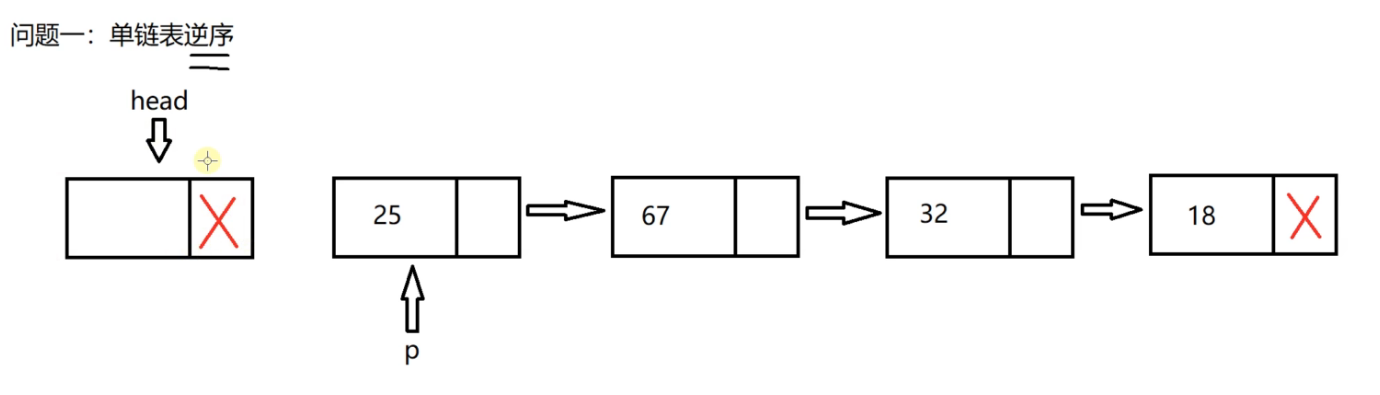
We can define a pointer p to the first valid node,

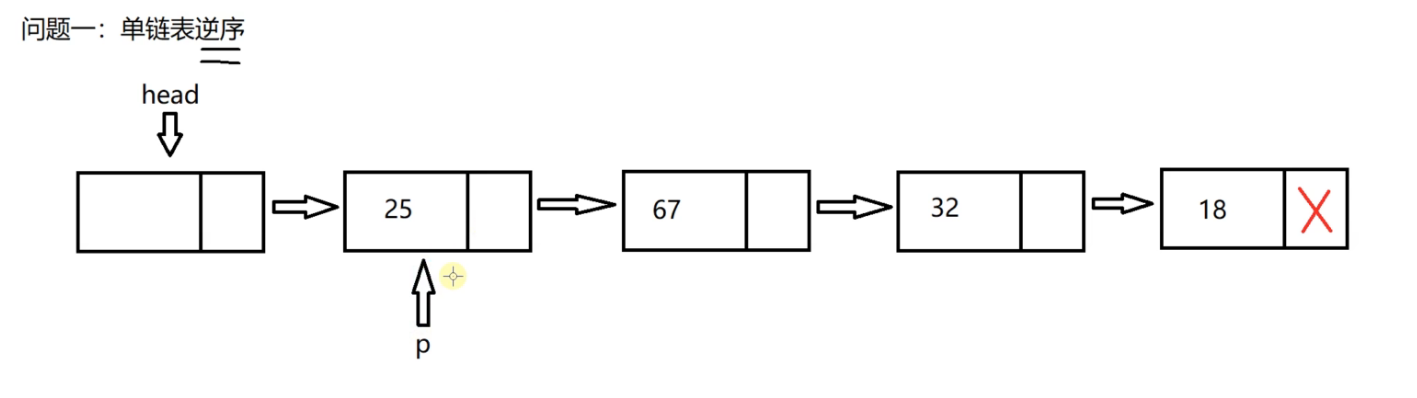
We need to remove the arrow in front of p. the next field of the head node will no longer record the address of the first valid node, and set the next field of the head node to be empty

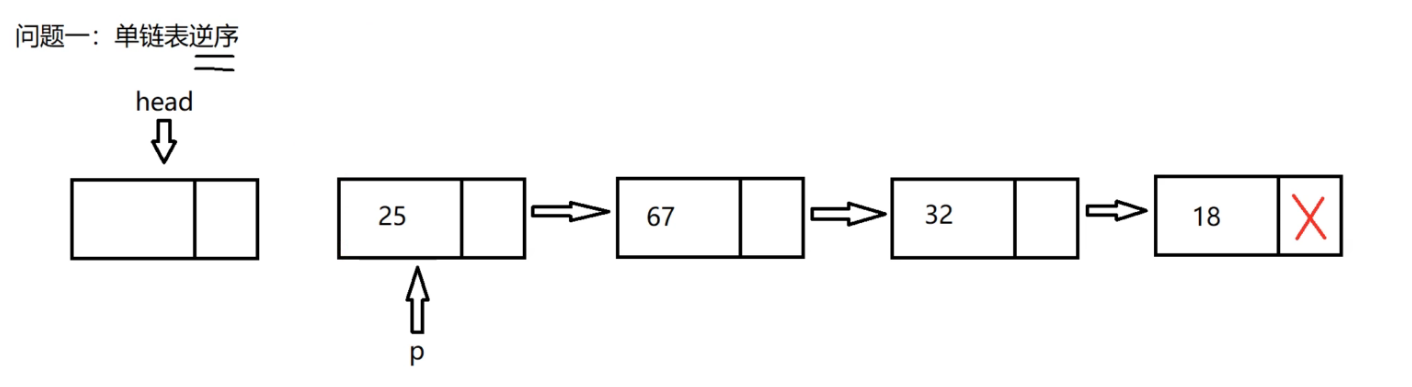
Now the head linked list is empty, leaving only the head node.

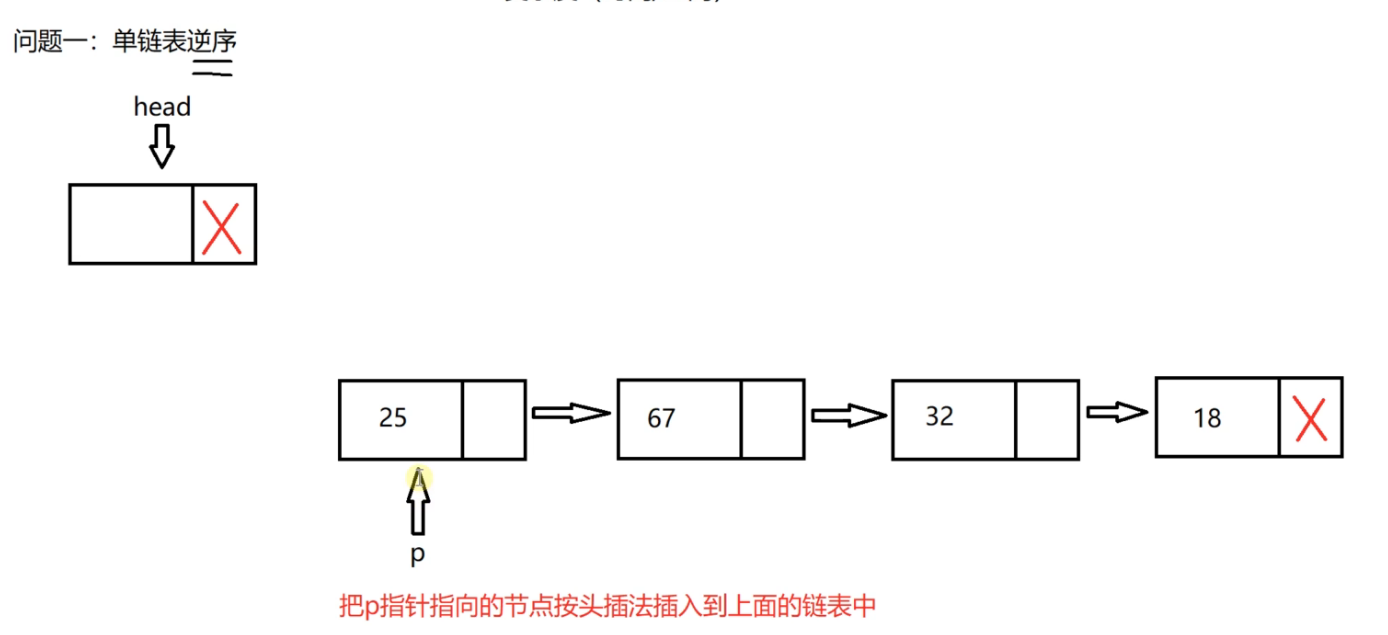
What we need to do now is to insert the node pointed to by p into the above linked list according to the head insertion method
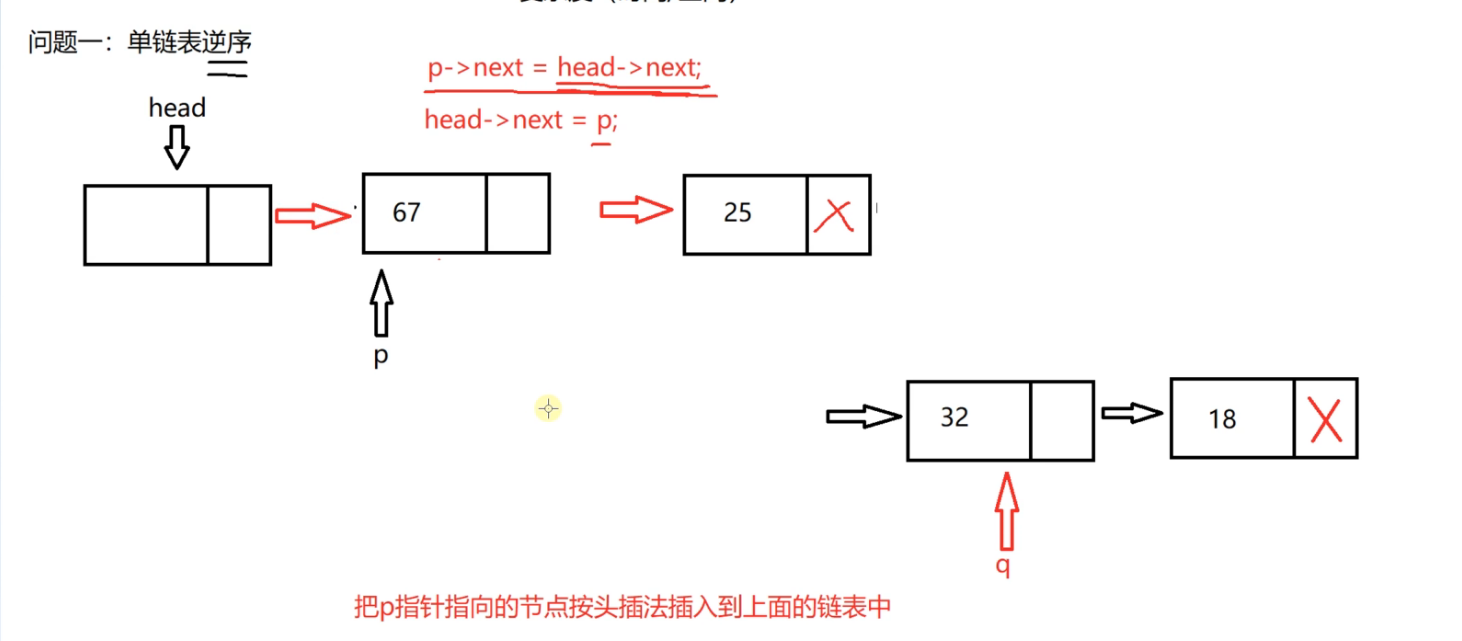
We need to remember the address of node 67 first, and then insert the 25 header


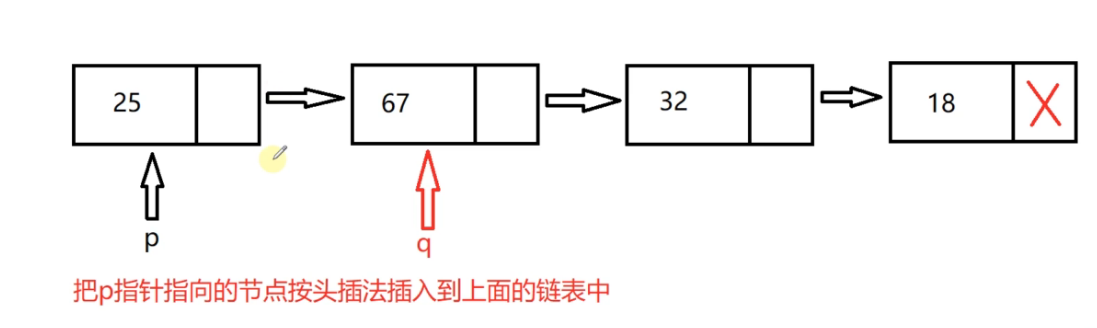
Then point p to Q, q = q - > next

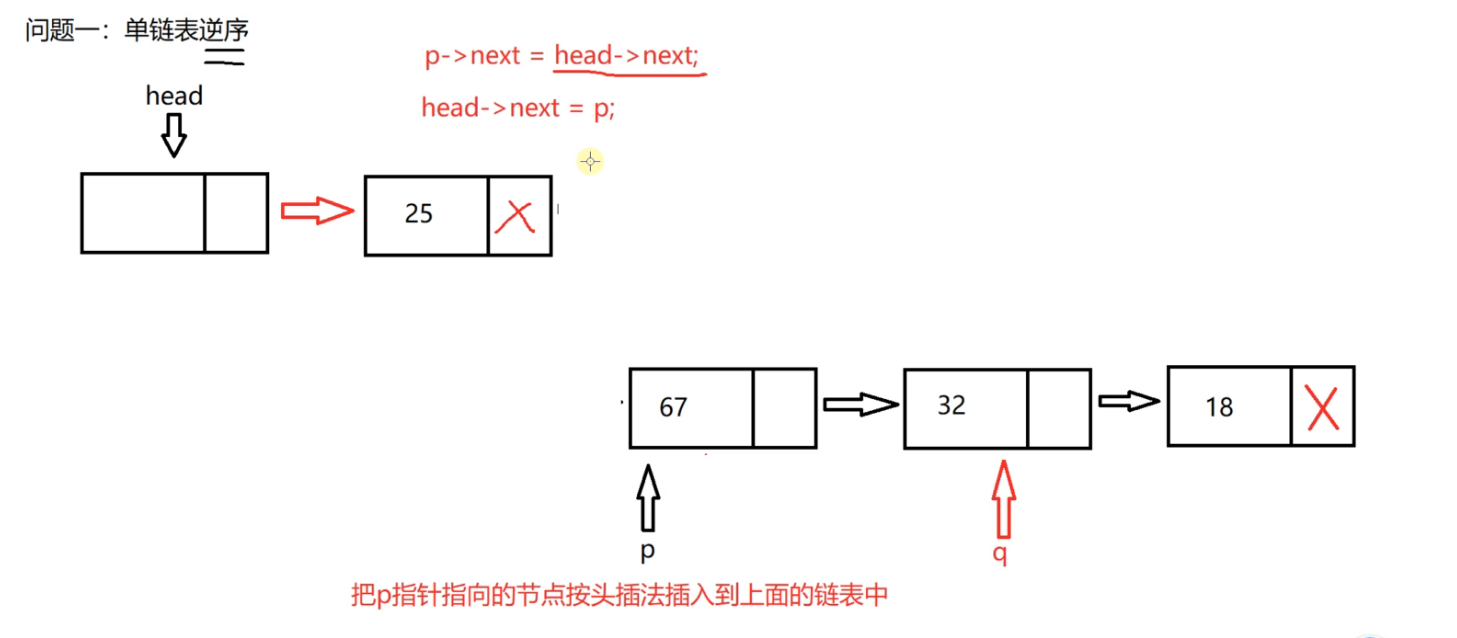
Then insert the node pointed to by p into the above linked list according to the header insertion method


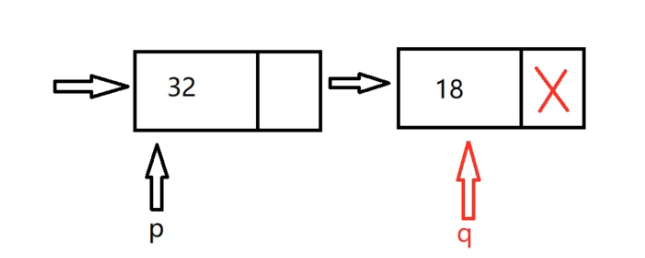
and so on

//Single linked list reverse order
void ReverseLink(Clink& link)
{
    Node* head = link.head_;
    Node* p = head->next_;
    if (p == nullptr)
    {
        return;
    }

    head->next_ = nullptr;

    while (p != nullptr)
    {
        Node* q = p->next_;

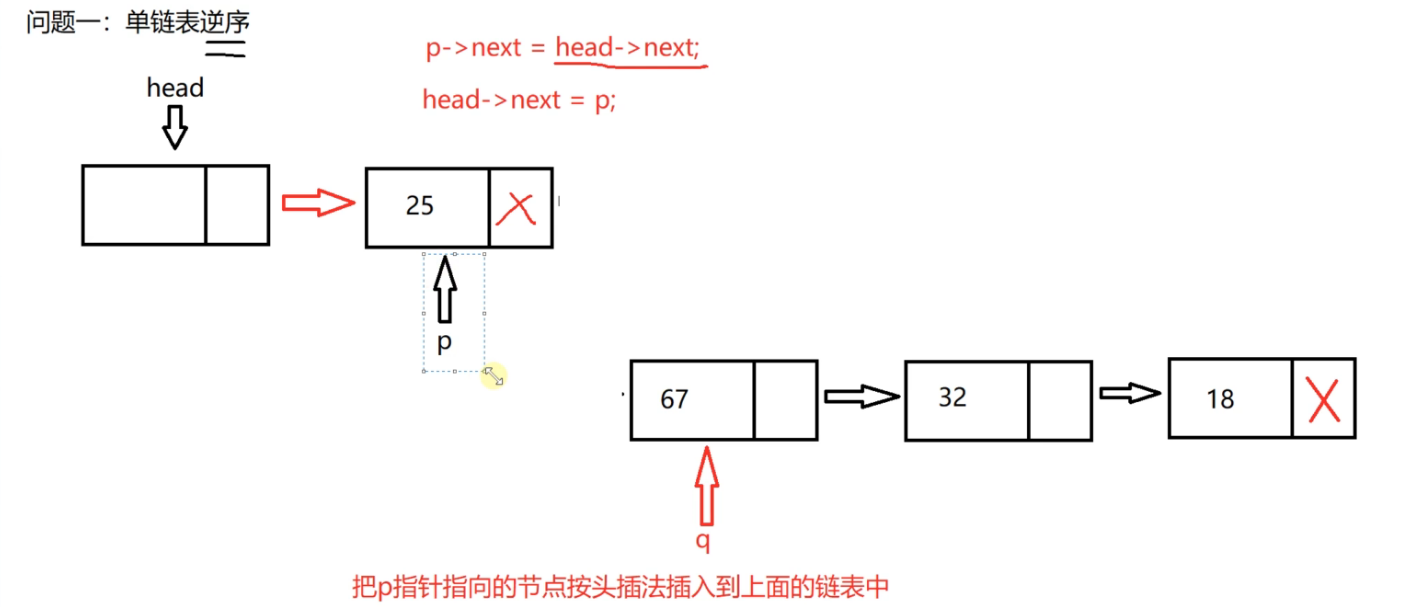
        //The node pointed to by the p pointer performs header insertion
        p->next_ = head->next_;
        head->next_ = p;

        p = q;
    }
}

Find the penultimate node in the single lin k ed list

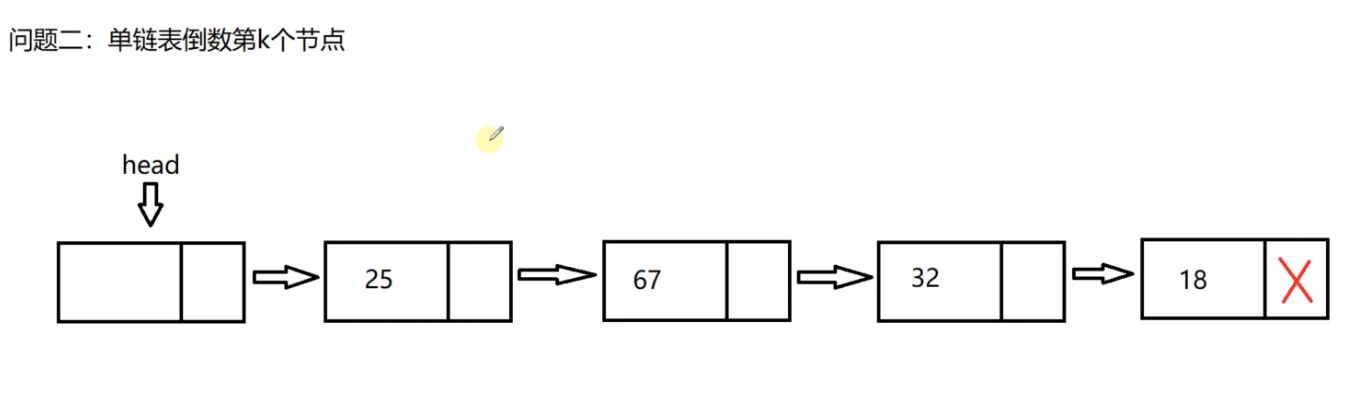
The penultimate node is 18, the penultimate node is 32, the penultimate node is 67, and the penultimate node is 65

The smaller the time complexity and space complexity, the better
It is impossible for a single linked list to traverse from back to front, so the tail pointer cannot be defined to point to the tail node
What can we do?
Method 1: open up an array to store these data, and then access the end of the array and subtract the subscript
This operation wastes space.
Method 2: traverse the linked list and count the number of nodes. The reciprocal number is positive: the total number - the reciprocal number, and then traverse the positive number from the node to access it
But if this linked list has 4 million nodes, looking for the penultimate third, don't you want to traverse all nodes, and then traverse (4 million - 3) nodes from the beginning. The linked list has been traversed twice in total. The longer the linked list, the more time we spend.

Method 3:
Double pointer thought
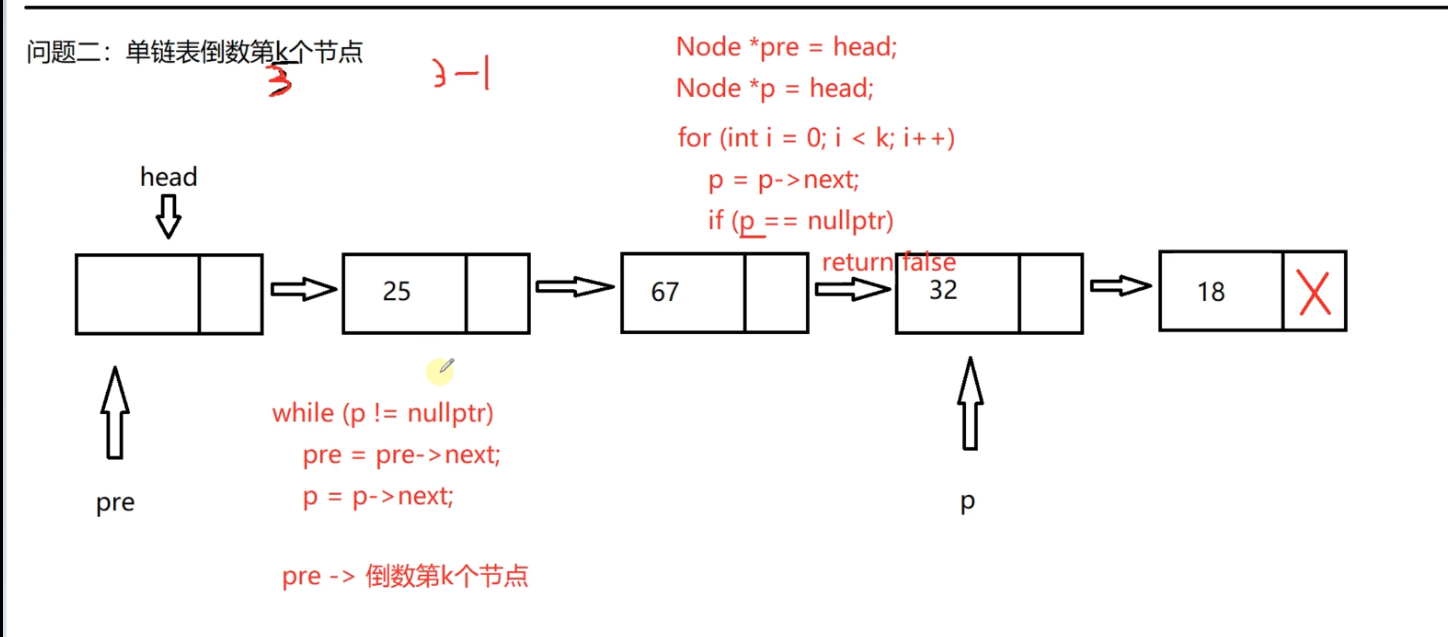
Define a pointer pre to the head node and a pointer p to the head node

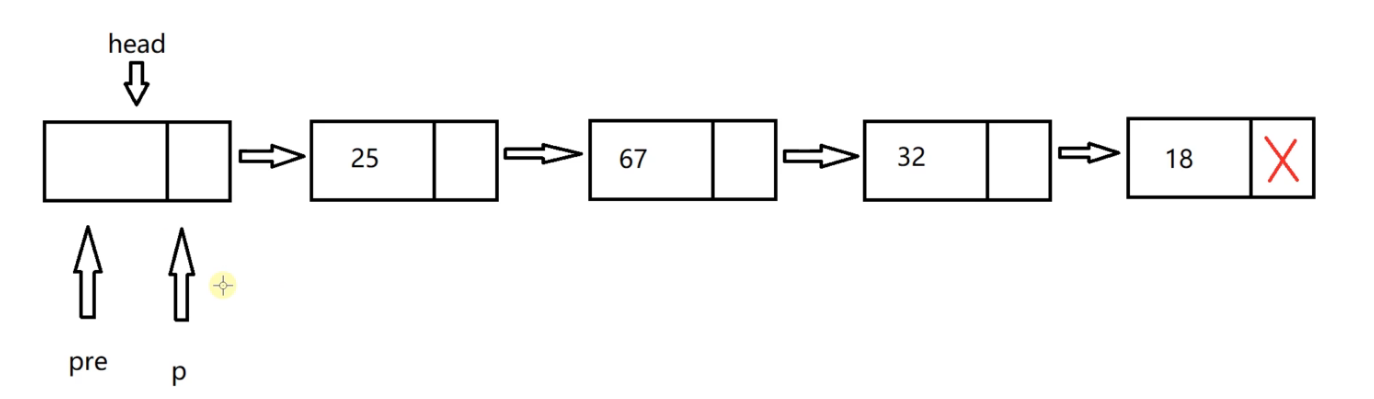
If you want to find the last k node, let p point to the positive k node first
Suppose you want to find the penultimate node, k=3
Let p point to the third node of the positive number, that is, p goes (k=3) times and pre doesn't move

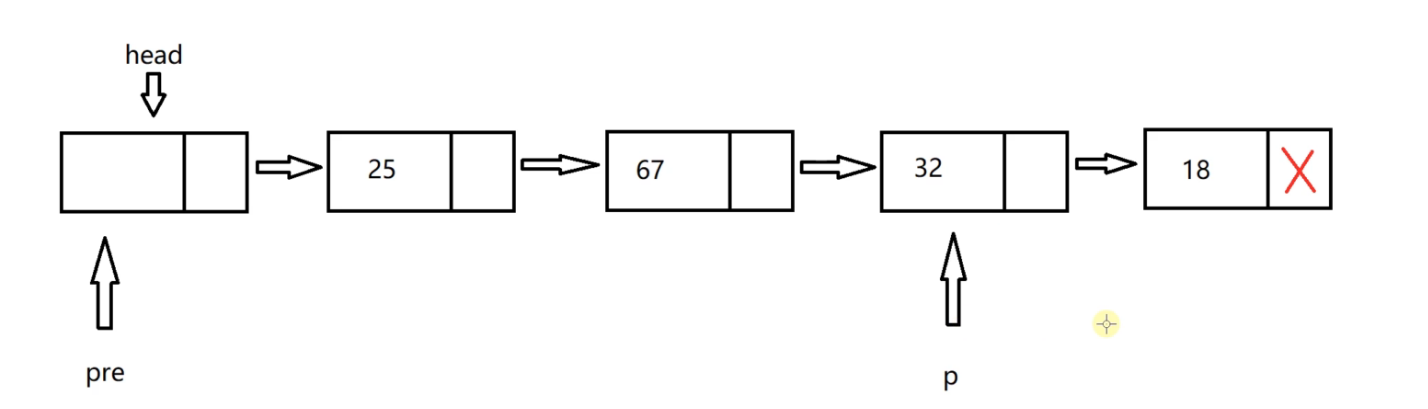
Now pre and p go together. Let's go together first

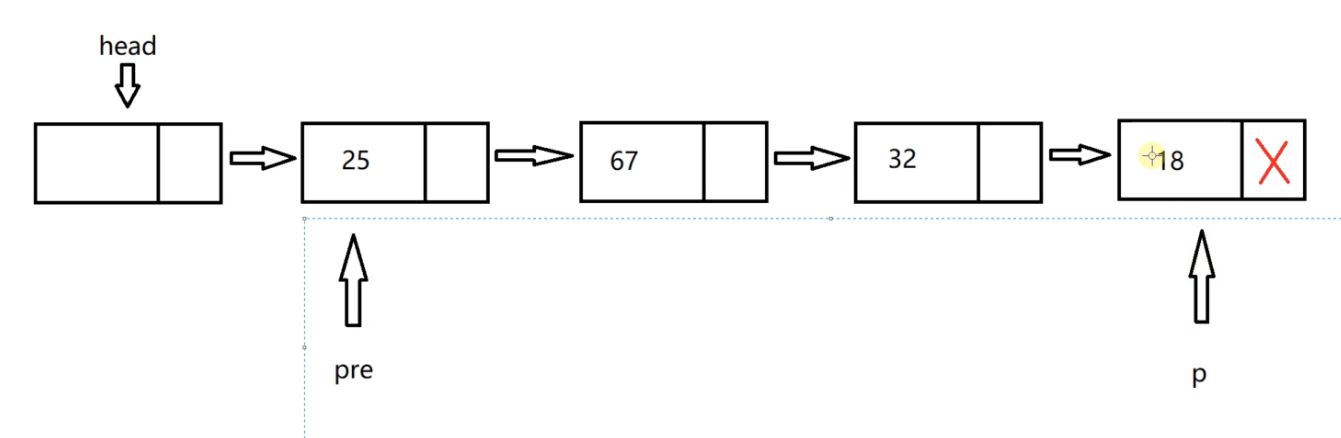
p points to the end node, and then pre and p continue

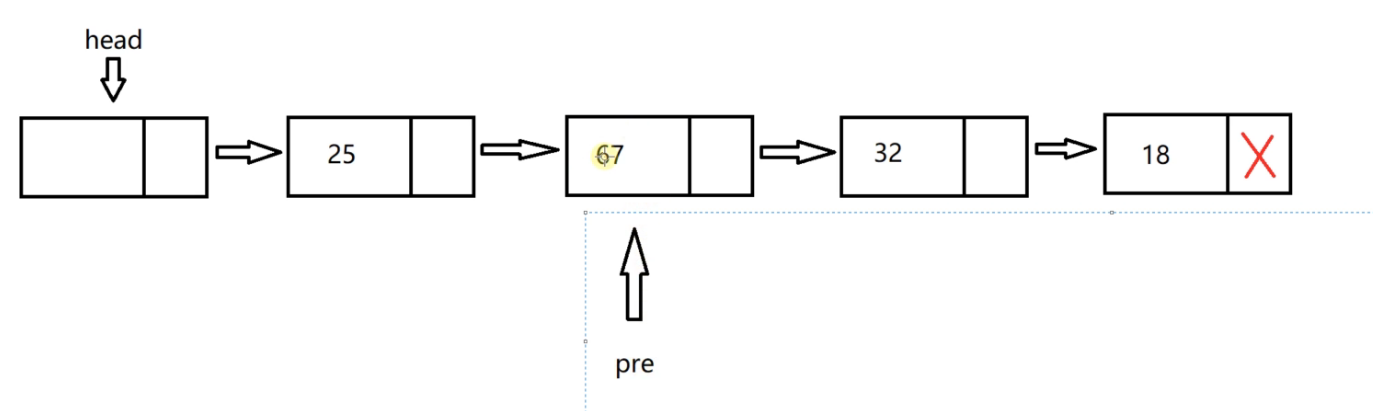
When p is empty, we can see that when p is empty, pre just points to the penultimate node '

If P and pre are initialized to point to the first valid node, first determine that P is empty, then p goes back (k-1) nodes, and then p and pre go back together until P is empty. Pre points to the penultimate node

//Find the value of the penultimate node
bool GetLaskKNode(Clink& link, int k, int& val)
{
    Node* head = link.head_;
    Node* pre = head;
    Node* p = head;

    if (k < 1)
    {
        return false;
    }

    for (int i = 0; i < k; i++)
    {
        p = p->next_;
        if (p == nullptr)
        {
            return false;//The positive number k does not exist, and the penultimate k naturally does not exist
        }
    }

    //At this time, pre is at the head node and p is at the k-th positive node, entering the while loop
    while (p != nullptr)
    {
        pre = pre->next_;
        p = p->next_;
    }

    val = pre->data_;
    return true;
}

Merge two ordered single linked tables

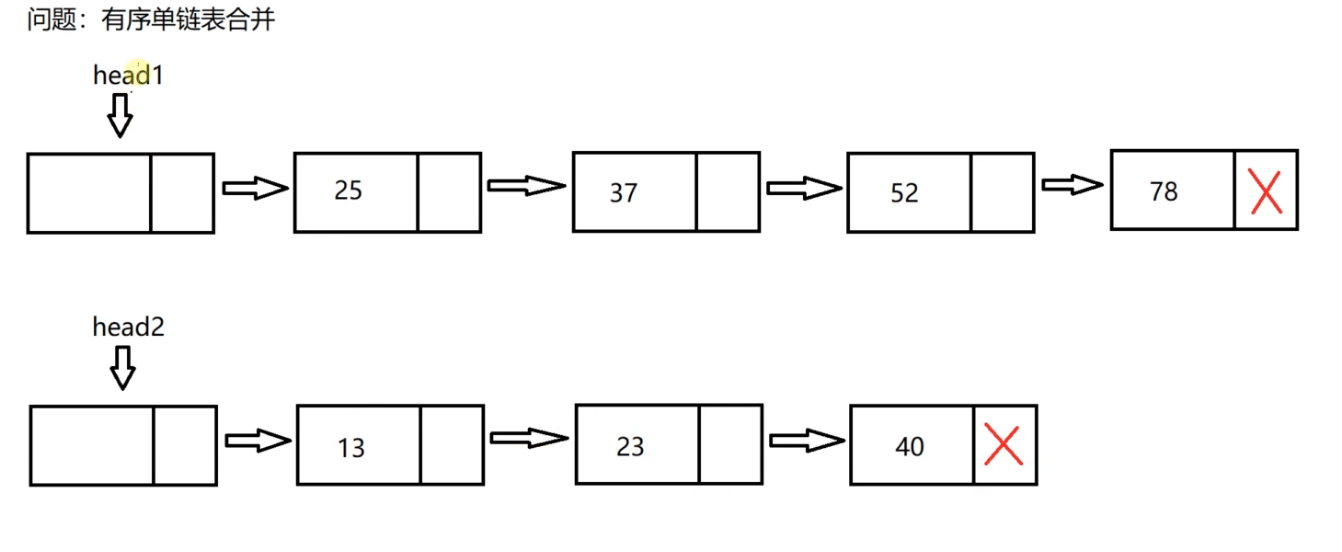
The two single linked lists are ordered. Now merge the two single linked lists in order on the first single linked list, and the final result is also ordered. Just set the second single linked list as an empty linked list
Connect the two linked lists according to the ordered nodes, connect the whole long linked list after the head node of the first linked list, and set the second single linked list as an empty linked list

Three pointer thought
One pointer p traverses the nodes of linked list 1, and one pointer q traverses the nodes of linked list 2,
Because the valid nodes of the two single linked lists are merged, these two pointers can access the first valid node of the two linked lists.

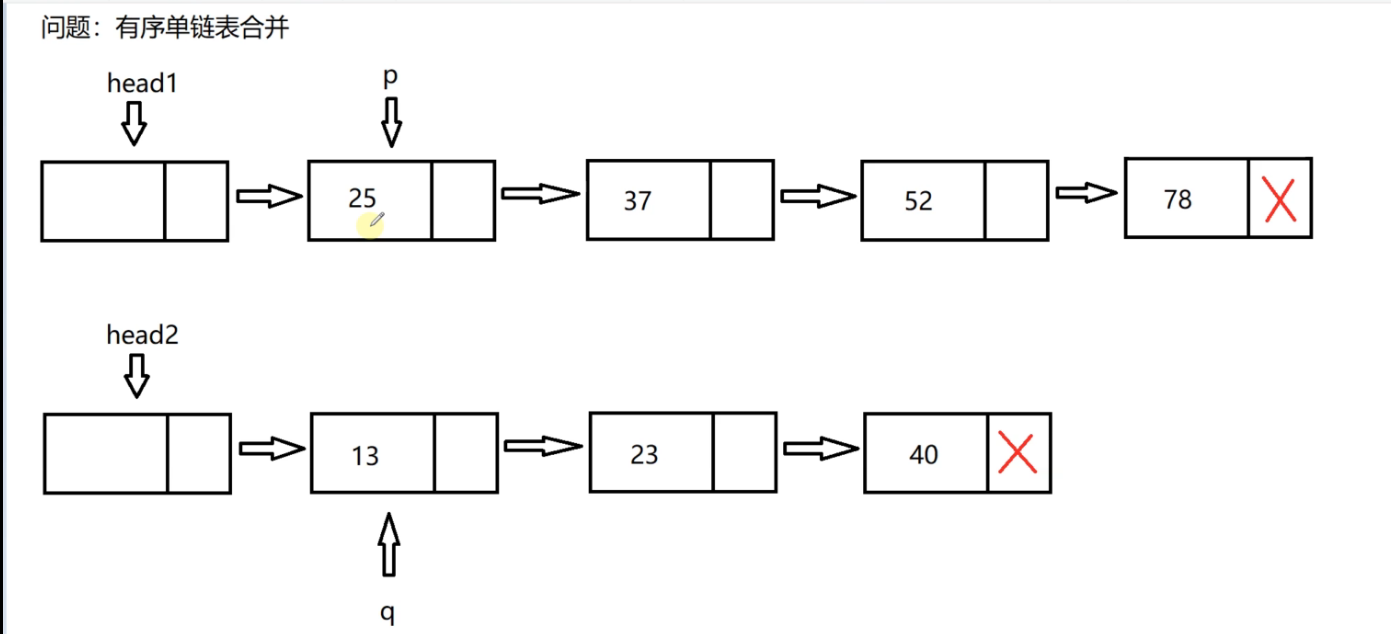
Because it is the last merged linked list, it is hung behind the head node of the first linked list.
The head1 pointer cannot be moved.
We define a last pointer to the currently connected end node, and the initialization pointer is the head node of linked list 1

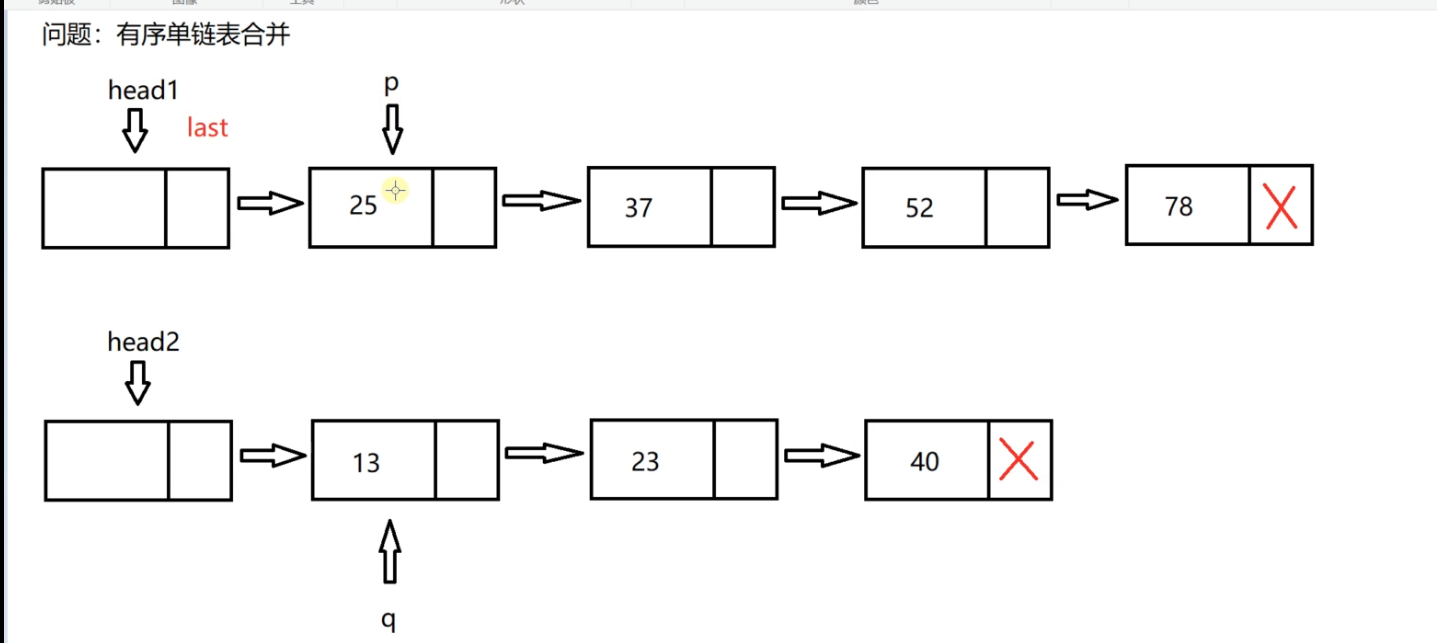
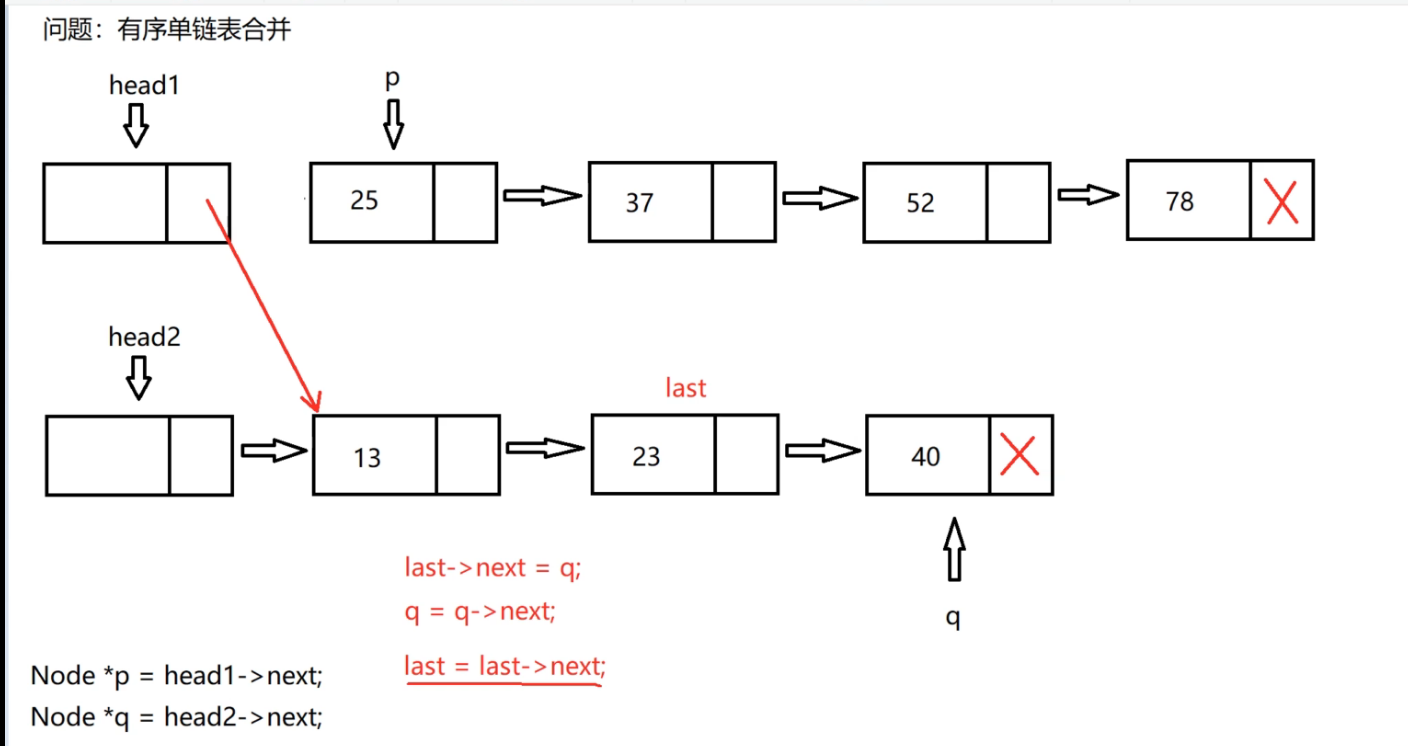
Then compare the data fields of p and q pointing to the node. If 25 is greater than 13, hang the node pointed to by q pointer behind last

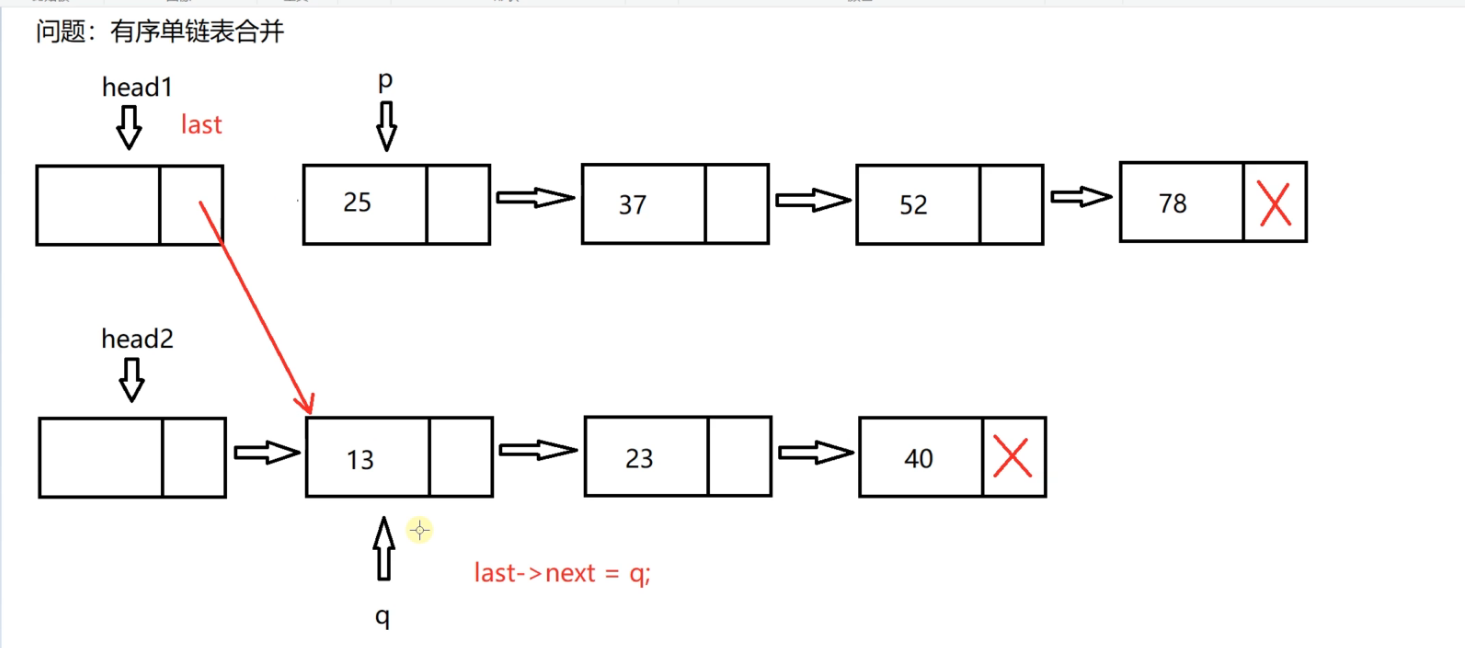
Then q = q - > next
Then the last pointer moves back one position


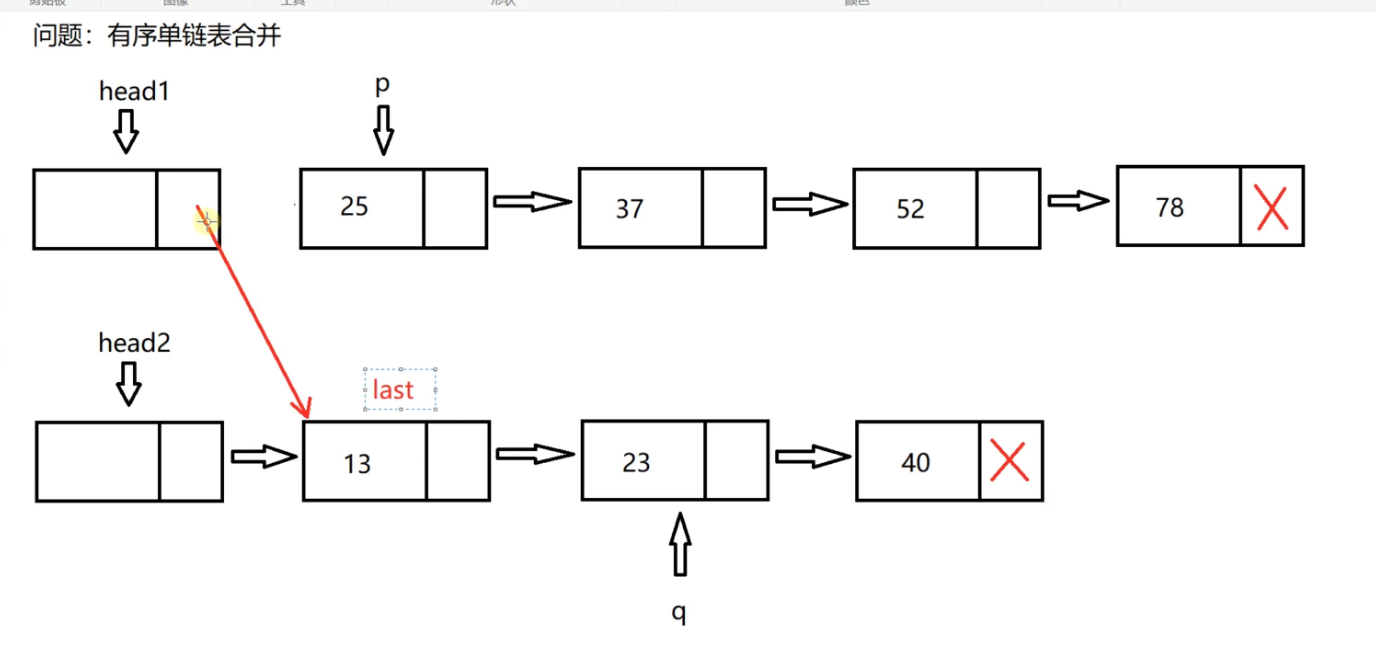
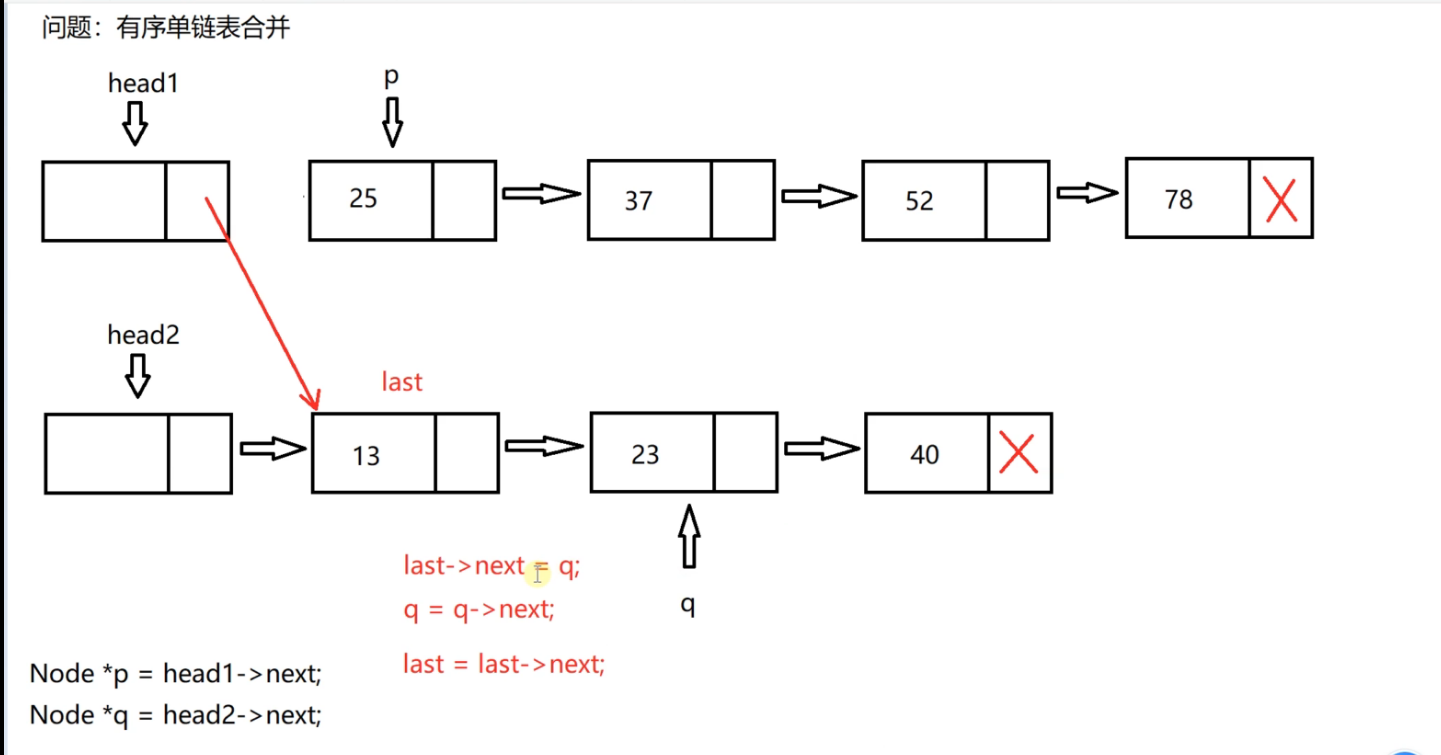
Then go on, p and q compare, and q is small, so go on doing the same thing


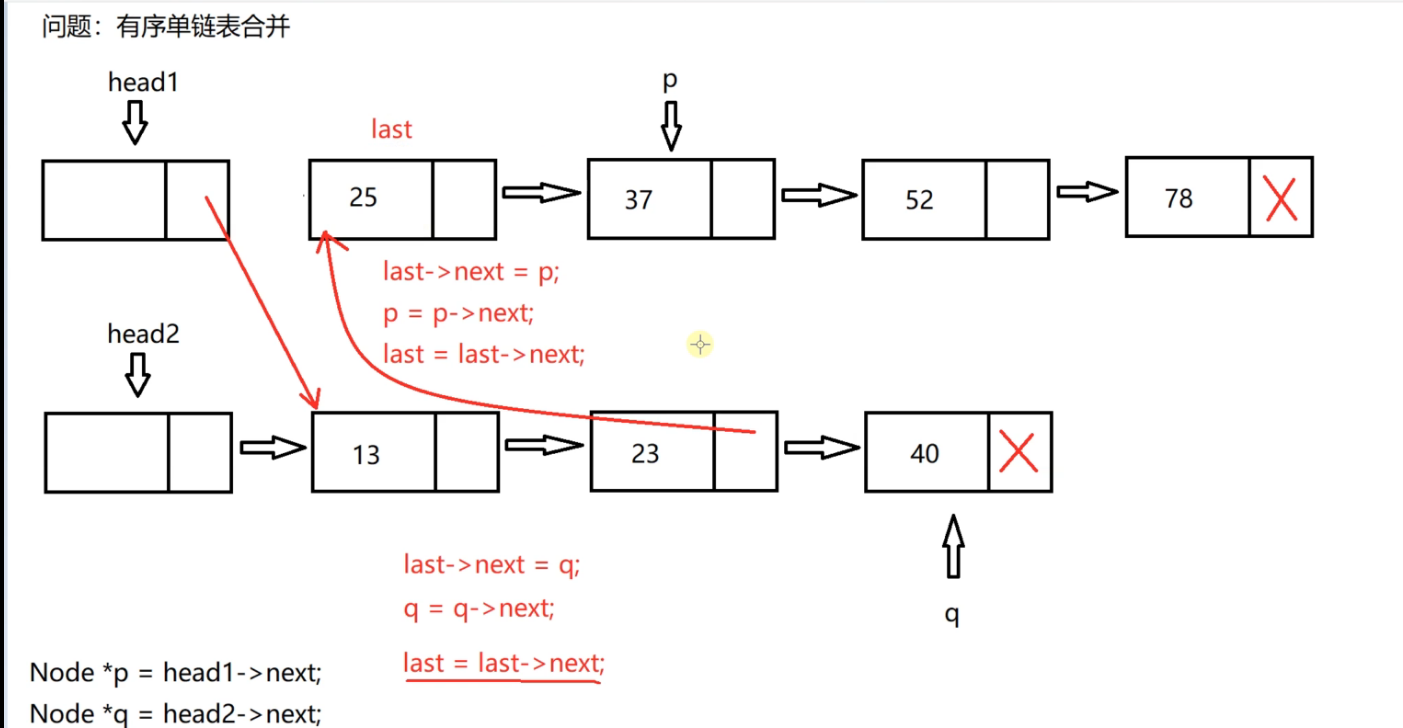
Then p and q are compared. When p is smaller, connect the node to which p points


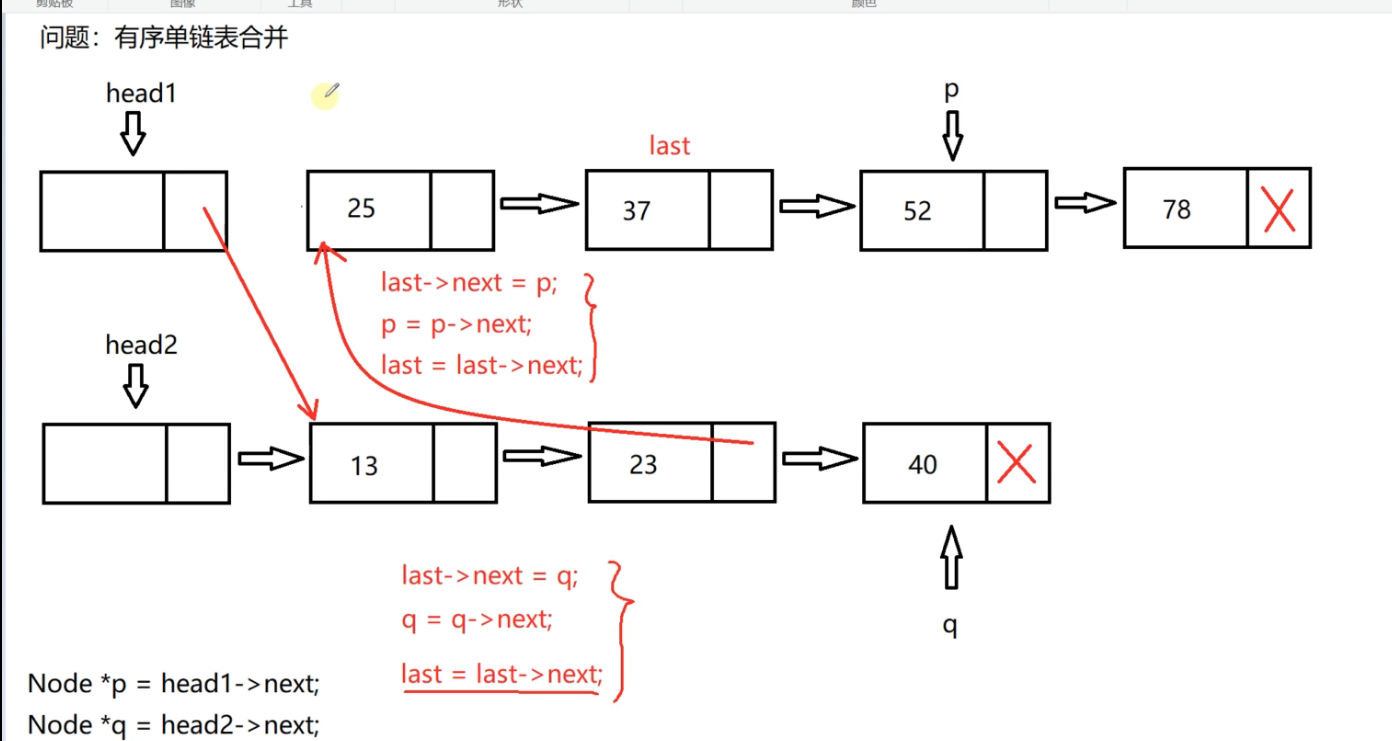
Then p and q are compared, P is small, and the node pointed to by P is connected

Then compare p with Q, q is small, and connect the node pointed to by Q

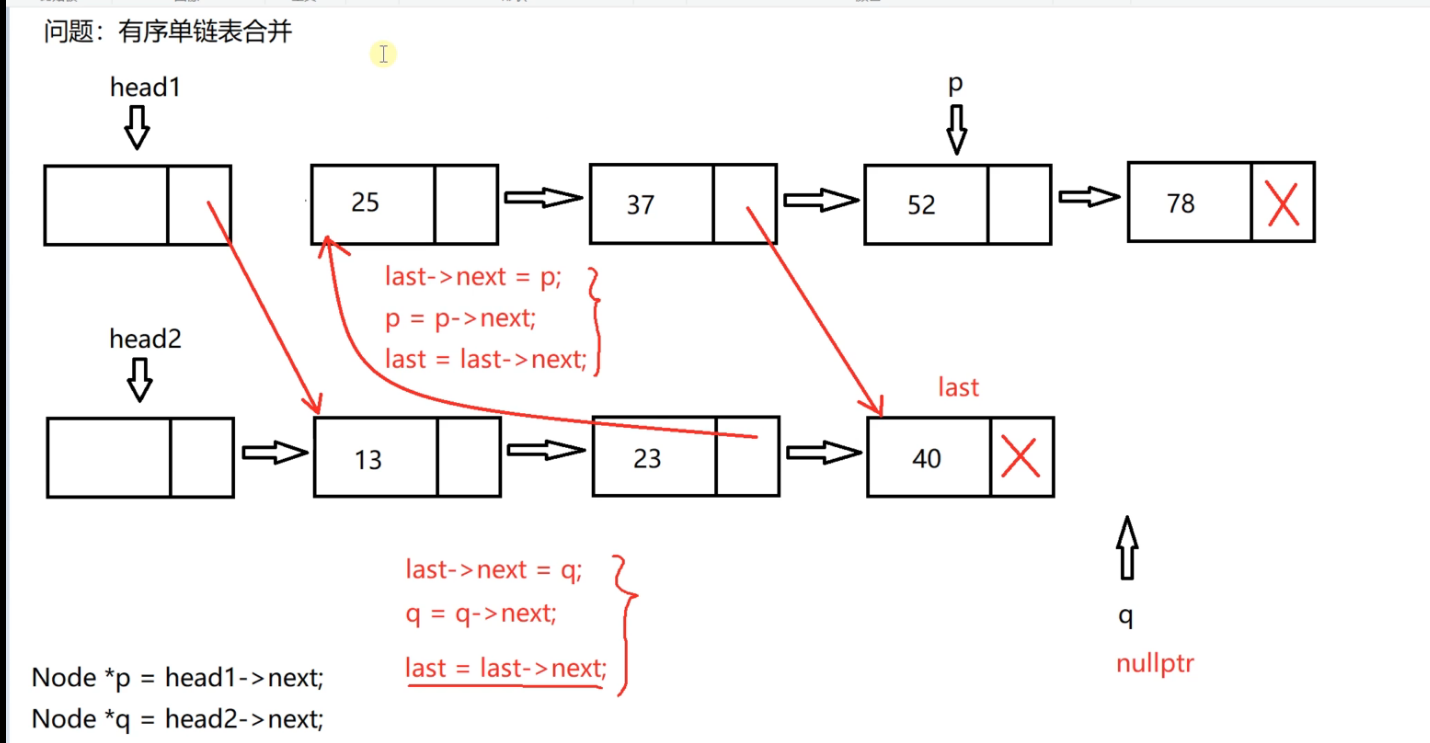
Now q points to null, p and q can't be compared
Therefore, we have a while loop condition:

When two linked lists, one of them traverses to empty.
If q is empty first, that's what happened just now.

That's OK!


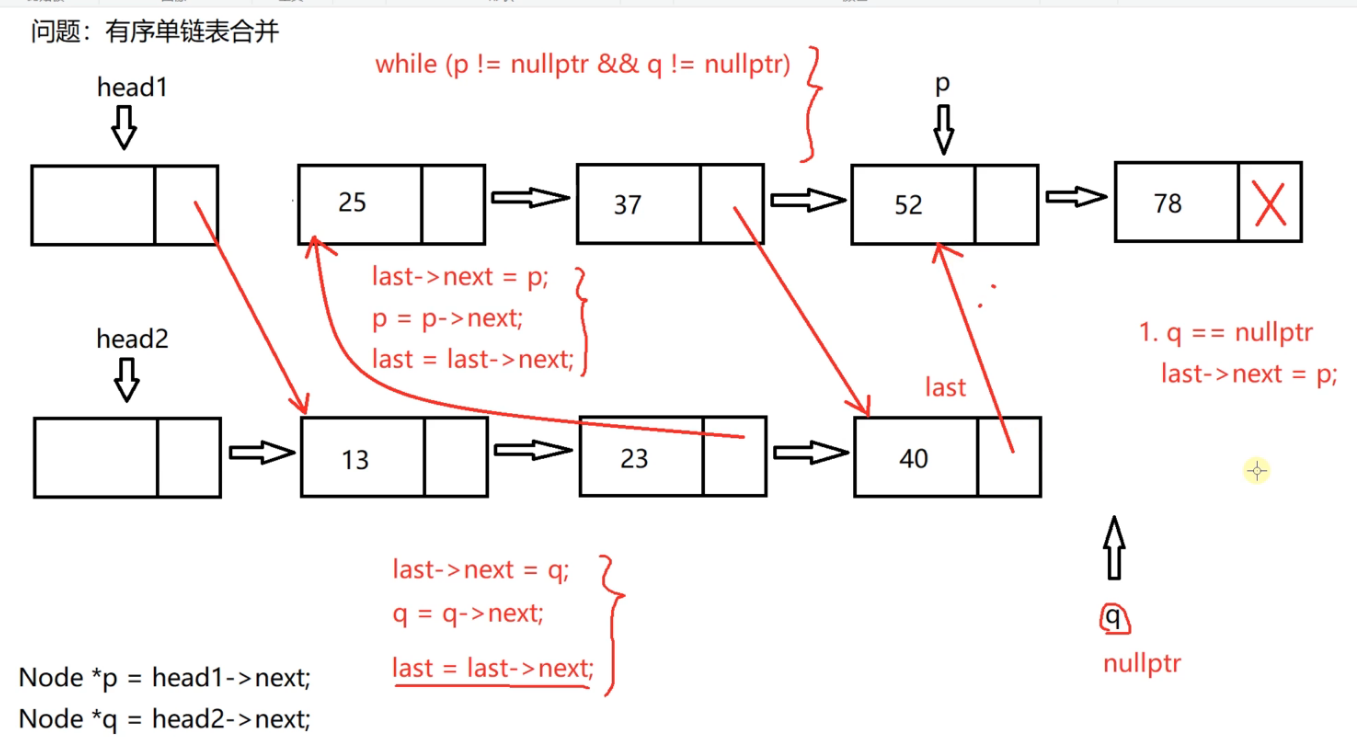
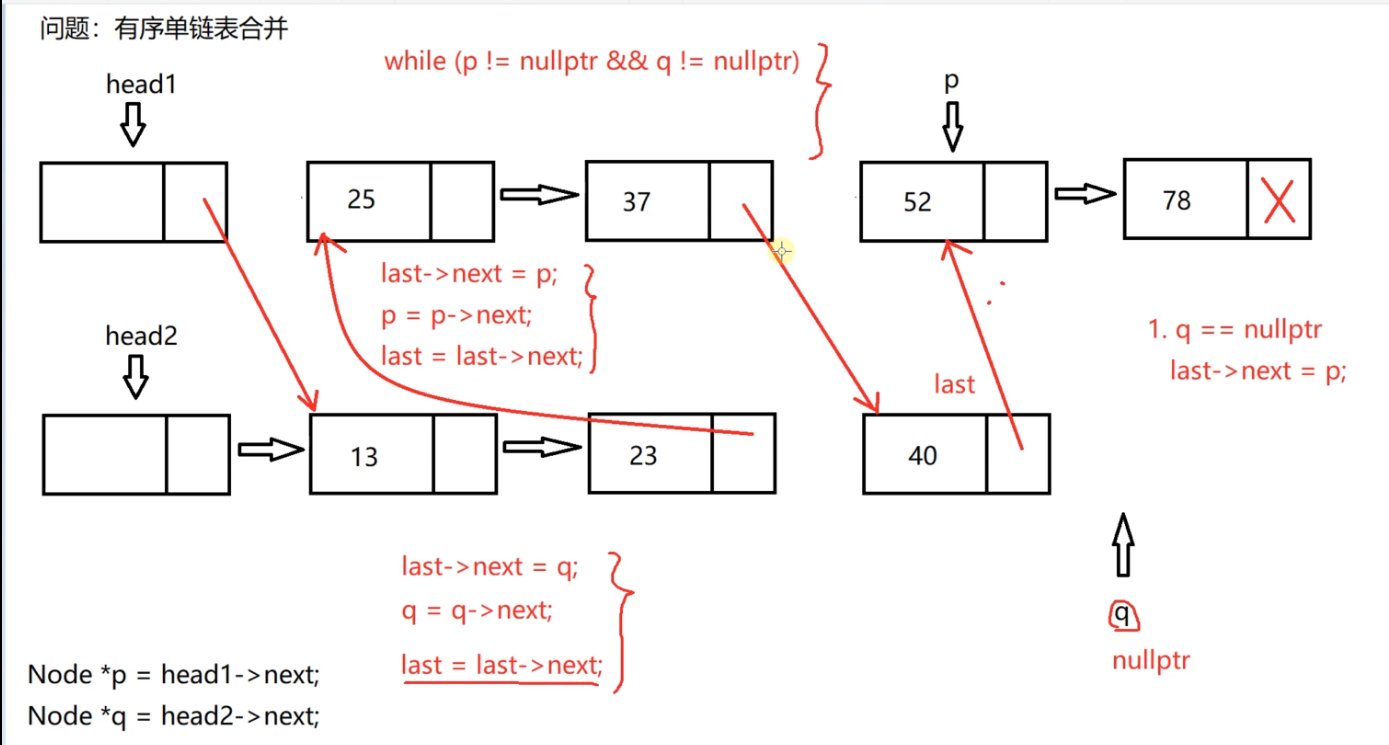
If p is empty first

That's it!

//Merge two ordered single linked tables
void MergeLink(Clink& link1, Clink& link2)
{
    Node* p = link1.head_->next_;
    Node* q = link2.head_->next_;
    Node* last = link1.head_;
    link2.head_->next_ = nullptr;

    while (p != nullptr && q != nullptr)
    {
        if (p->data_ < q->data_)
        {
            last->next_ = p;
            p = p->next_;
            last = last->next_;
        }
        else
        {
            last->next_ = q;
            q = q->next_;
            last = last->next_;
        }
    }

    if (p != nullptr)
    {
        last->next_ = p;
    }
    else
    {
        last->next_ = q;
    }
}