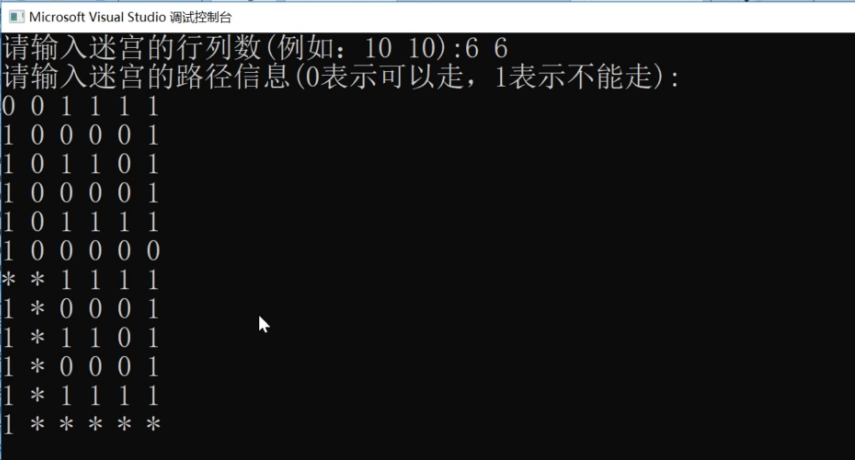
Find the shortest path of the maze
How to find the shortest path in the maze???

Use the breadth traversal maze path to search for the shortest path:
0 0 1 1 1 1 1 0 0 0 0 1 1 0 1 1 0 1 1 0 0 0 0 1 1 0 1 1 1 1 1 0 0 0 0 0
Breadth first traversal to find the shortest path

If the value of (0,0) is 1, it means that the intersection of the maze is sealed and can be return ed directly.
If the value of (0,0) is 0, it means that the intersection is open. Put 0 in the queue.
Then start the loop. If the queue is not empty, see whether the right side of the team head element can go. If it can go, put the right element into the team,

Then we have to see whether the lower, left and upper sides of the (0,0) element can go or not. This (0,0) element is processed and out of the team.

Then, now the team head is the second element in the first row. First, modify its left side and the right side of (0,0) to be unable to go, then see whether the right side of this element can go or not, see whether the following elements can go or not, and then the following elements will join the team.

Then the team head element also depends on whether the left side can go, can't go, can't go above, can't go, and then after processing, it's out of the team.

This node is the second node in the second row
Then see if it can go on the right, can go, and the elements on the right join the team.

Now the new element is the end of the queue. The head of the queue, that is, the original element, needs to continue to judge, and join the team with all the elements that can go in all directions. Now see whether the lower elements can go, can go, and the lower elements can also join the team,

Then see if the left side can go, can't go, can't go above, can't go, and then get out of the team.

The current queue head element is the element in the second row and the third column. The queue tail element is the element in the second column of the third row.
Then continue to look at the team head element to see if it can go on the right. If it can go, the right element will join the team

It can't go below, left or above. If you take the team head element out of the team.

The current queue head is the second column element in the third row, and the queue tail element is the fourth column element in the second row.
And so on.
Layer upon layer expansion

In the queue, when a node is queued, we find that if the end of the queue element is the node in the lower right corner, it proves that the maze path has reached the node in the lower right corner.
The walking status of all nodes is recorded in the queue, but the previous nodes have been out of the queue and are not in the queue.
Problems with this queue:

The queue can only find the shortest path. However, the path information of the shortest path cannot be recorded.

How much space can we open up? We can only use the size of the worst-case space to open up.
An array of rows multiplied by the size of columns

When we reach the node in the lower right corner, we find the exit. We have to record which nodes are in the maze path. We need to record that the node in the lower right corner comes from the node on its left. How to record?
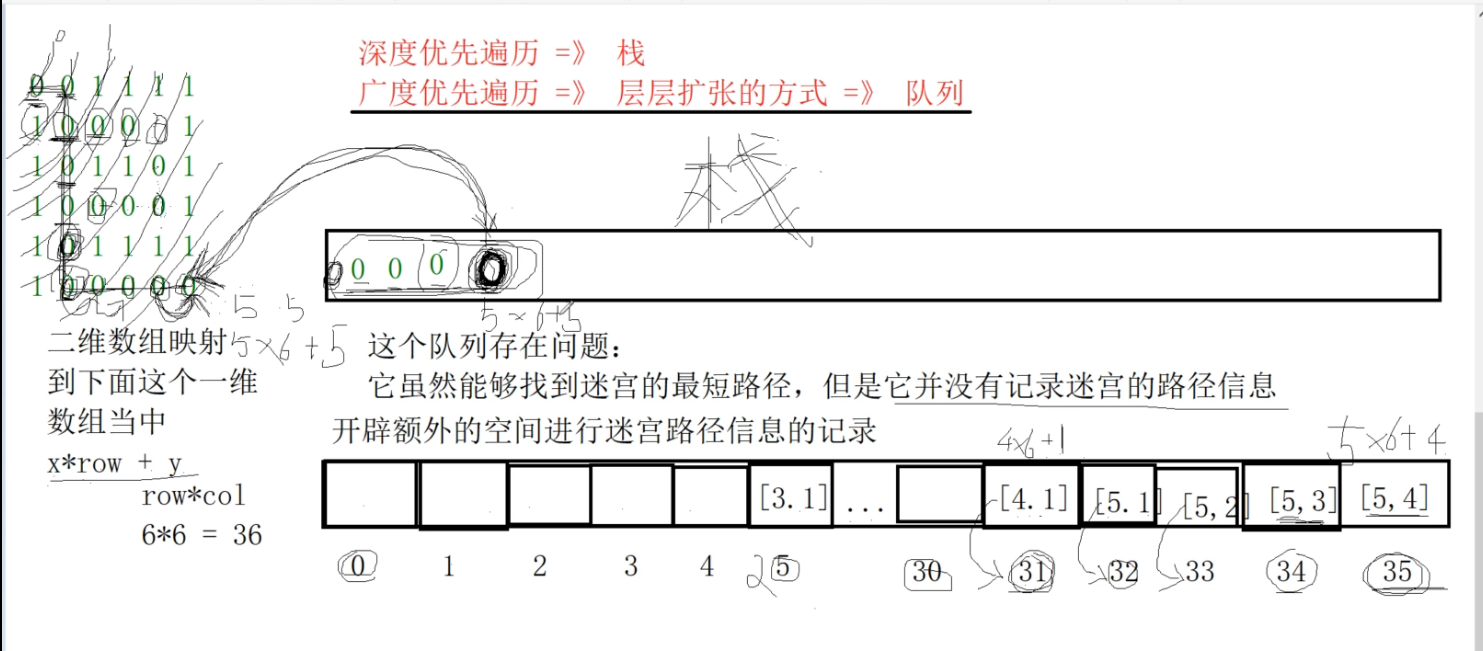
Maze is a two-dimensional array. In fact, it is a one-dimensional array in memory, so we map this two-dimensional array to the following one-dimensional array.
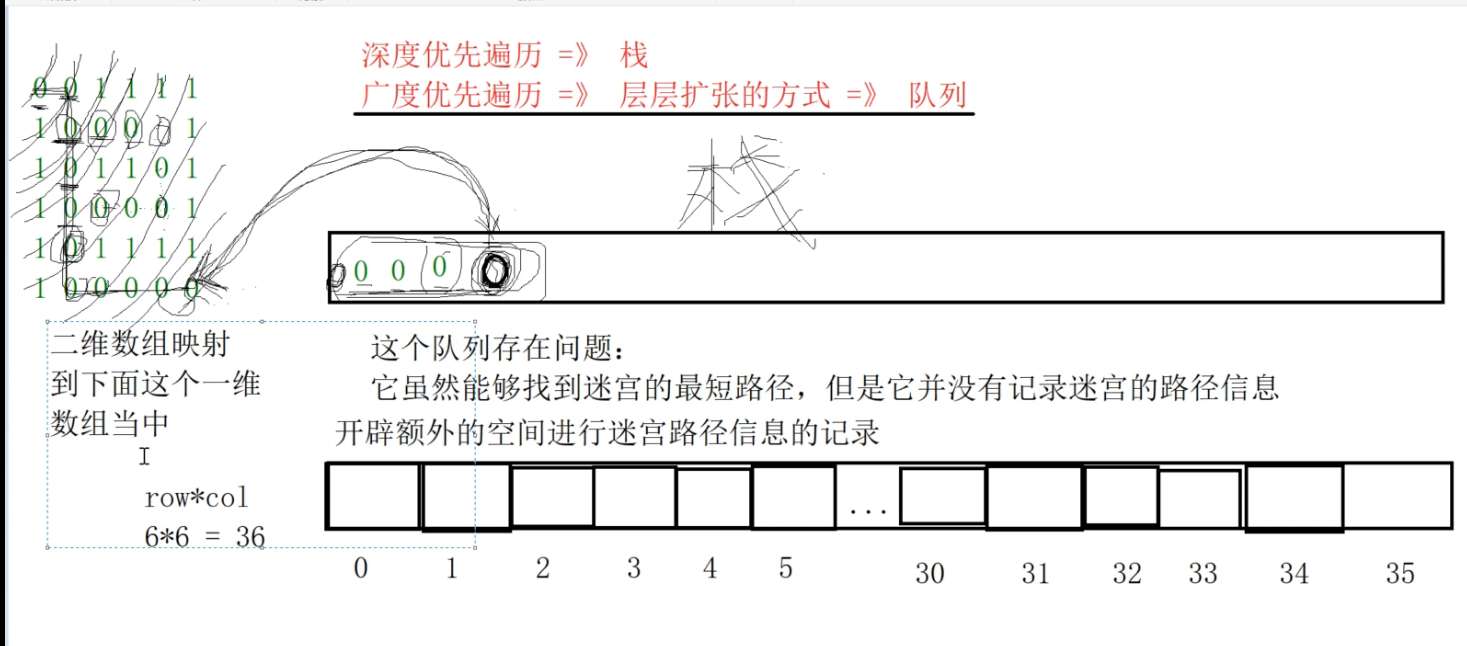
The formula for mapping the subscript of a two-dimensional array to a one-dimensional array is as follows:

Then, in which direction the current node is going, record this information, record it in the one-dimensional array position corresponding to the node it is going to go, and record: which node the current node comes from. Then push forward until the entry node (0,0) is found, and the path information of the shortest maze path will come out.
code implementation
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
//Define direction
const int RIGHT = 0;
const int DOWN = 1;
const int LEFT = 2;
const int UP = 3;
const int WAY_NUM = 4;
//Define walking status
const int YES = 4;
const int NO = 5;
//maze
class Maze
{
public:
Maze(int row, int col)
:_row(row)
, _col(col)
{
_pMaze = new Node*[_row];//Open maze two-dimensional array
for (int i = 0; i < _row; ++i)
{
_pMaze[i] = new Node[_col];
}
//node._x*_row + node._y
_pPath.resize(_row * _col);//Auxiliary array space
}
void initNode(int x, int y, int val)//Initialize to No
{
_pMaze[x][y]._x = x;
_pMaze[x][y]._y = y;
_pMaze[x][y]._val = val;
for (int i = 0; i < WAY_NUM; ++i)
{
_pMaze[x][y]._state[i] = NO;
}
}
void setNodeState()//Set maze walking status
{
for (int i = 0; i < _row; ++i)
{
for (int j = 0; j < _col; ++j)
{
if (_pMaze[i][j]._val == 1)
{
continue;
}
if (j < _col - 1 && _pMaze[i][j + 1]._val == 0)
{
_pMaze[i][j]._state[RIGHT] = YES;
}
if (i < _row - 1 && _pMaze[i + 1][j]._val == 0)
{
_pMaze[i][j]._state[DOWN] = YES;
}
if (j > 0 && _pMaze[i][j - 1]._val == 0)
{
_pMaze[i][j]._state[LEFT] = YES;
}
if (i > 0 && _pMaze[i - 1][j]._val == 0)
{
_pMaze[i][j]._state[UP] = YES;
}
}
}
}
void searchMazePath()//Breadth first traversal search
{
if (_pMaze[0][0]._val == 1)
{
return;
}
_queue.push(_pMaze[0][0]);//Entry node queue
while (!_queue.empty())//Queue is not empty
{
Node front = _queue.front();//Get queue header element
int x = front._x;
int y = front._y;
//Right direction
if (_pMaze[x][y]._state[RIGHT] == YES)
{
_pMaze[x][y]._state[RIGHT] = NO;
_pMaze[x][y + 1]._state[LEFT] = NO;
//Record the walking information of the node in the auxiliary array
_pPath[x*_row + y + 1] = _pMaze[x][y];
_queue.push(_pMaze[x][y + 1]);
if (check(_pMaze[x][y + 1]))
return;
}
//Down direction
if (_pMaze[x][y]._state[DOWN] == YES)
{
_pMaze[x][y]._state[DOWN] = NO;
_pMaze[x + 1][y]._state[UP] = NO;
_pPath[(x + 1)*_row + y] = _pMaze[x][y];
_queue.push(_pMaze[x + 1][y]);
if (check(_pMaze[x + 1][y]))
return;
}
//Left direction
if (_pMaze[x][y]._state[LEFT] == YES)
{
_pMaze[x][y]._state[LEFT] = NO;
_pMaze[x][y - 1]._state[RIGHT] = NO;
_pPath[x*_row + y - 1] = _pMaze[x][y];
_queue.push(_pMaze[x][y - 1]);
if (check(_pMaze[x][y - 1]))
return;
}
//Up direction
if (_pMaze[x][y]._state[UP] == YES)
{
_pMaze[x][y]._state[UP] = NO;
_pMaze[x - 1][y]._state[DOWN] = NO;
_pPath[(x - 1)*_row + y] = _pMaze[x][y];
_queue.push(_pMaze[x - 1][y]);
if (check(_pMaze[x - 1][y]))
return;
}
//Current node out of queue
_queue.pop();
}
}
void showMazePath()//Print maze
{
if (_queue.empty())
{
cout << "There is no maze path!" << endl;
}
else
{
//Backtracking to find maze path nodes
int x = _row - 1;
int y = _col - 1;
for (;;)
{
_pMaze[x][y]._val = '*';
if (x == 0 && y == 0)
break;
Node node = _pPath[x*_row + y];
x = node._x;
y = node._y;
}
for (int i = 0; i < _row; ++i)
{
for (int j = 0; j < _col; ++j)
{
if (_pMaze[i][j]._val == '*')
{
cout << "* ";
}
else
{
cout << _pMaze[i][j]._val << " ";
}
}
cout << endl;
}
}
}
private:
//Define maze node path information
struct Node
{
int _x;
int _y;
int _val;//The value of the node
int _state[WAY_NUM];//Record the status of the node in four directions
};
//Check whether it is the labyrinth exit node in the lower right corner
bool check(Node &node)
{
return node._x == _row - 1 && node._y == _col - 1;
}
Node **_pMaze;//Dynamic 2D array
int _row;//that 's ok
int _col;//column
queue<Node> _queue;//Breadth traversal dependent queue structure
vector<Node> _pPath;//Record the walking information of nodes and auxiliary array during breadth first traversal
};
int main()
{
cout << "Please enter the number of rows and columns of the maze(For example: 10 10):";
int row, col, data;
cin >> row >> col;
Maze maze(row, col);//Create maze object
cout << "Please enter the path information of the maze(0 It means you can go, and 1 means you can't go):" << endl;
for (int i = 0; i < row; ++i)
{
for (int j = 0; j < col; ++j)
{
cin >> data;
//You can initialize the basic information of the maze node
maze.initNode(i, j, data);
}
}
//Start setting the status of all nodes in four directions
maze.setNodeState();
//Start searching the path information of the maze from the upper left corner
maze.searchMazePath();
//Print maze path search results
maze.showMazePath();
return 0;
}