1. Problem Description:

Let the middle order traversal of a binary tree with n nodes be (1, 2, 3,..., n), where the numbers 1, 2, 3,..., n are the node numbers. Each node has a score (all positive integers). Note that the score of the ith node is di, and each subtree of the tree and its subtree has a bonus. The bonus calculation method of any subtree (including the tree itself) is as follows:
Bonus points of left subtree of subtree × The bonus of the right subtree of the subtree + the score of the root of the subtree. If a subtree is empty, the bonus is 1. The bonus of a leaf is the score of the leaf node itself, regardless of its empty subtree.
Try to find a binary tree that conforms to the middle order and traverses (1,2,3,..., n) with the highest bonus.
Required output:
(1) The highest bonus of tree
(2) Preorder traversal of tree

Input format

Line 1: an integer n, which is the number of nodes. Line 2: n integers separated by spaces, which is the score of each node (0 < score < 100).

Output format

Line 1: an integer, which is the highest bonus (the result will not exceed the int range). Line 2: n integers separated by spaces, traversing the preceding order of the tree. If there are multiple schemes, the scheme with the smallest dictionary order is output.

Data range

n < 30

Input example:

5
5 7 1 2 10

Output example:

145
3 1 2 4 5
Source: https://www.acwing.com/problem/content/description/481/

2. Train of thought analysis:

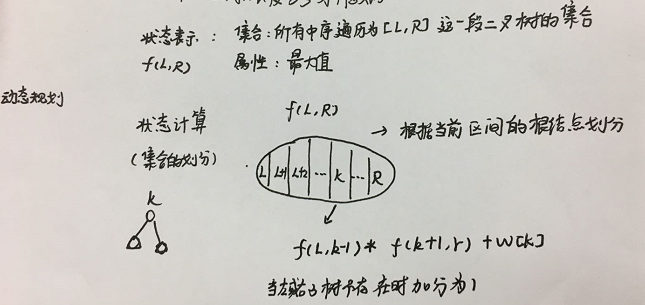
From the analysis of the problem, we can know that only one middle order traversal is given (1, 2, 3,..., n), so the form of the binary tree is not unique. What we solve is to find the binary tree with the highest bonus among all binary trees with middle order traversal of (1, 2, 3,..., n). Because the dictionary order is the smallest, this binary tree can uniquely determine the form, Therefore, we need to search all possibilities to find the best answer, so the current problem is an optimization problem, which can be solved by search or dynamic programming. The following is the idea of dynamic programming. Dynamic programming is generally divided into two steps: ① state representation; ② State calculation; We can declare a two-dimensional array dp, where dp[i][j] represents the maximum bonus of the set whose middle order traversal is [I, j]; How to calculate the state? The last difference is generally found in the division of the set corresponding to the state calculation. We can divide it according to which number of the root node of the binary tree corresponding to the current interval is in the interval. The root node of the binary tree can be any number in the interval [I, j]. We can enumerate all the root nodes in the current interval to solve the maximum bonus of each set, Because the maximum bonus points are recorded in the two-dimensional dp array, and the topic also needs to output the preorder traversal order of the scheme corresponding to the maximum bonus points, the current two-dimensional array dp cannot record the scheme. Like the previous solution, we can declare an additional two-dimensional array g to record the root node corresponding to the maximum bonus points in the interval [I, j], Because the root nodes of the interval are enumerated from small to large, the dictionary order must be the smallest when updating. We update the root node of the current interval only when the bonus is greater. In this way, we use array g to record the root node with the maximum bonus of each interval, and then we use recursion to output the corresponding preorder traversal order of the root node, As like as two peas, each time is divided into [l, k - 1] and [k + 1, r] to process. Combined with G array, you can get the root node of the largest score in the interval.

3. The code is as follows:

from typing import List

class Solution:
    # Recursively output the preorder traversal corresponding to the root node
    def dfs(self, l: int, r: int, g: List[List[int]]):
        if l > r: return
        # According to the current root node, it can be divided into two intervals
        k = g[l][r]
        print(k, end=" ")
        self.dfs(l, k - 1, g)
        self.dfs(k + 1, r, g)


    def process(self):
        n = int(input())
        # Add a 0 in front of the list, so that the stored element subscripts start from 1 and will be easier to handle later
        a = [0] + list(map(int, input().split()))
        dp = [[0] * (n + 1) for i in range(n + 1)]
        # g is used to record the root node that can obtain the maximum bonus points in the current interval
        g = [[0] * (n + 1) for i in range(n + 1)]
        for l in range(1, n + 1):
            i = 1
            while i + l - 1 <= n:
                j = i + l - 1
                if l == 1:
                    dp[i][j] = a[i]
                    g[i][j] = i
                else:
                    # The root node can be the endpoint of the left and right intervals. If it is the endpoint, the score will be 1
                    for k in range(i, j + 1):
                        left = 1 if k == i else dp[i][k - 1]
                        right = 1 if k == j else dp[k + 1][j]
                        score = left * right + a[k]
                        # If the scores are equal, the root node at the beginning is the one with the smallest dictionary order
                        if score > dp[i][j]:
                            dp[i][j] = score
                            g[i][j] = k
                i += 1
        print(dp[1][n])
        self.dfs(1, n, g)


if __name__ == "__main__":
    Solution().process()