time

September 24, 2021

subject

In the multi-level bidirectional linked list, in addition to the pointer to the next node and the previous node, it also has a sub linked list pointer, which may point to a separate bidirectional linked list. These sub lists may also have one or more of their own sub items, and so on to generate multi-level data structures, as shown in the following example.

Give you the head node at the first level of the list. Please flatten the list so that all nodes appear in the single level double linked list.

Example 1

Input: head = [1,2,3,4,5,6, null, null, 7,8,9,10, null, null, 11,12]
Output: [1,2,3,7,8,11,12,9,10,4,5,6]
Explanation:

The entered multi-level list is shown in the following figure:

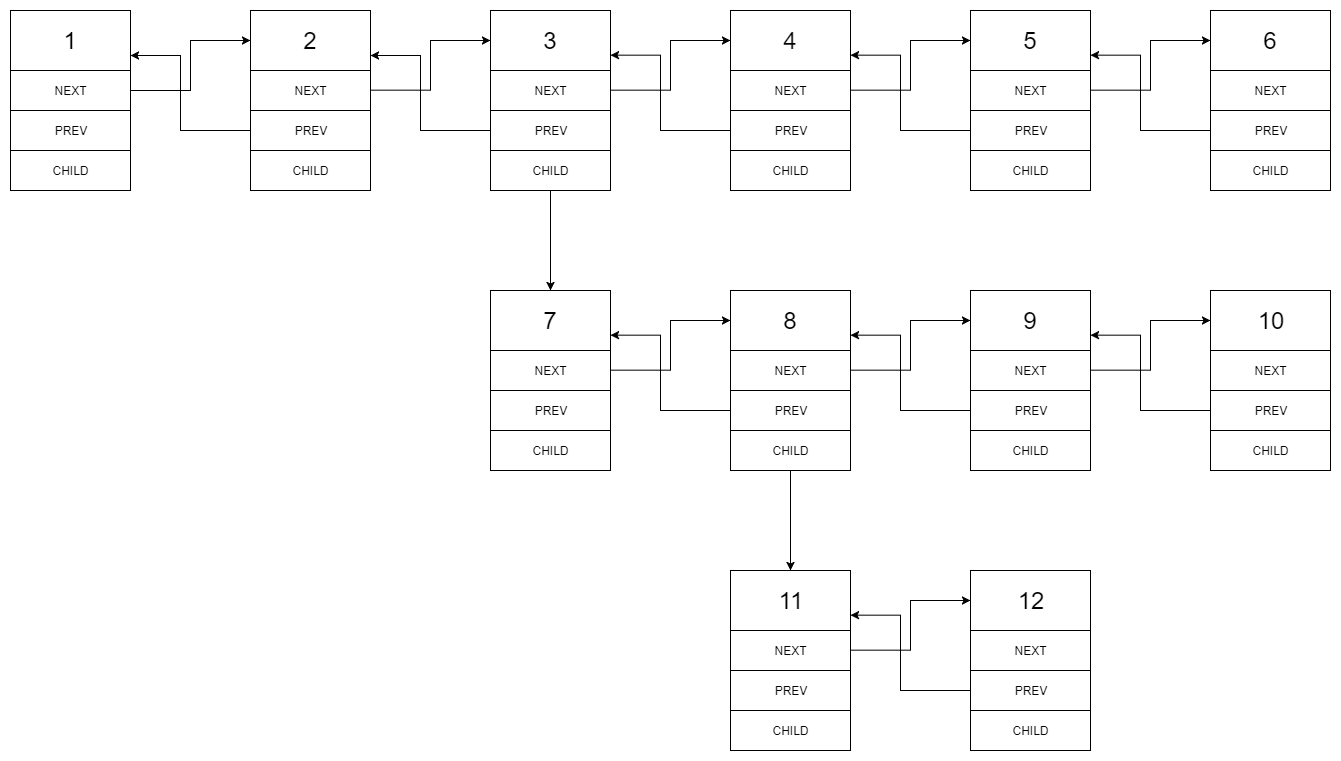
The flattened linked list is shown in the following figure:

 

 

Example 2:

Input: head = [1,2,null,3]
Output: [1,3,2]
Explanation:

The entered multi-level list is shown in the following figure:

  1---2---NULL
  |
  3---NULL

Example 3:

Input: head = []
Output: []

How to represent a multi-level linked list in a test case?

with   Example 1   For example:

 1---2---3---4---5---6--NULL
         |
         7---8---9---10--NULL
             |
             11--12--NULL

After serializing each of these levels:

[1,2,3,4,5,6,null]
[7,8,9,10,null]
[11,12,null]

In order to serialize each level together, we need to add a null element in each level to indicate that no node is connected to the parent node of the previous level.

[1,2,3,4,5,6,null]
[null,null,7,8,9,10,null]
[null,11,12,null]

Merge all serialization results and remove null at the end.

[1,2,3,4,5,6,null,null,null,7,8,9,10,null,null,11,12]

Tips:

• The number of nodes shall not exceed 1000
• 1 <= Node.val <= 10^5

answer

First answer (see the official)

Use DFS (depth first search)

/*
// Definition for a Node.
class Node {
    public int val;
    public Node prev;
    public Node next;
    public Node child;
};
*/

class Solution {
    public Node flatten(Node head) {
       dfs2(head);
       return head;
    }
    public  Node dfs2 (Node head){
        Node cur = head;
        Node last = null;
        
        while(cur != null){
            Node next = cur.next;
            if(cur.child != null){
                Node lastChild = dfs2(cur.child);
//                Connects the current node to its child nodes
                cur.next = cur.child;
                cur.child.prev = cur;
//                If next is not empty, the last child node will be connected to the next node
                if(next!=null){
                    next.prev = lastChild;
                    lastChild.next = next;
                }
                
//                Set child to null
                cur.child = null;
                last = lastChild;
            }else {
                last = cur;
            }
            cur = next;
            
        }
        return last;
    }
}

Idea:

Traverse nodes. If there are child nodes, traverse the child nodes first. Point the parent's next to the first child, point the last child's next to the parent's original next, and set the parent's child to null

Second answer (own idea)

Traversal sequence using preorder

/*
// Definition for a Node.
class Node {
    public int val;
    public Node prev;
    public Node next;
    public Node child;
};
*/

class Solution {
    public Node flatten(Node head) {
        calc(head);
        return head;
    }
    public void calc(Node head){
        Node r = head;
        Stack stack = new Stack();
        stack.push(r);
        if(r==null){
            return;
        }
        Node preNode = null;
        while (!stack.isEmpty()){
            Node node = (Node)stack.pop();
            Node next = node.next;
            if(preNode != null){
                node.prev = preNode;
                preNode.next = node;
                preNode = null;
            }
            if(next == null && node.child ==null){
                preNode = node;
            }
            if(next != null){
                stack.push(node.next);
            }
            if (node.child != null){
                stack.push(node.child);
                node.next = node.child;
                node.child.prev = node;
                node.child = null;
            }
        }
    }
}

Use the Stack first in and then out, and the next first in and then the child. If there is a child, first point the next of the parents to the first child, and the prev of the child to the parents. Before that, the child has been saved in the Stack, so it will not affect the later. At the same time, use the preNode to store the last child node, so that the next can be connected with the last child,