This tutorial is open source: GitHub Welcome fork

preface

In this tutorial, we will describe how to use KdTree to find the K nearest neighbors of a specific point or location, and how to find all neighbors within a radius specified by the user (random in this case).

Introduction to theory

kd tree or k-dimensional tree is a data structure used in computer science to organize a certain number of points in a k-dimensional space. It is a binary search tree with other constraints. kd tree is very useful for range and nearest neighbor search. For our purposes, we usually only deal with three-dimensional point clouds, so all our kd trees are three-dimensional. Each layer of the kd tree uses a hyperplane perpendicular to the corresponding axis to split all child nodes along a specific dimension. At the root of the tree, all child nodes will be split according to the first dimension (that is, if the first dimension coordinate is less than the root, it will be in the left subtree; if it is greater than the root, it will obviously be in the right subtree in the left subtree). Each layer in the tree is divided on the next dimension. Once all other dimensions are exhausted, it returns to the first dimension. The most effective way to build a kd tree is to use the partition method like Quick Sort, place the midpoint at the root, and put all the contents with small one-dimensional value on the left and large on the right. Then repeat this process on the left and right subtrees until the last tree to be partitioned consists of only one element.

From[ Wikipedia]: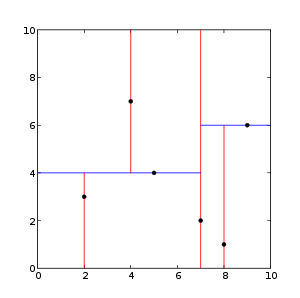

This is an example of a two-dimensional kd tree:

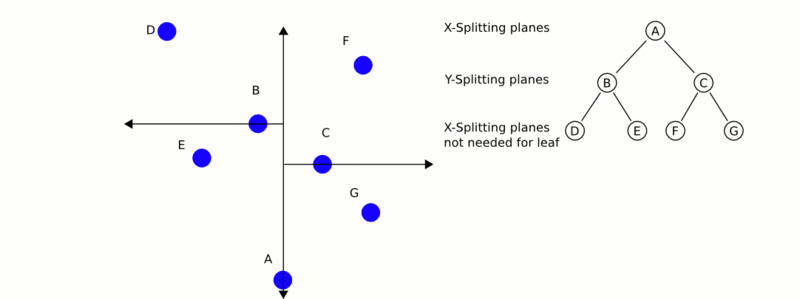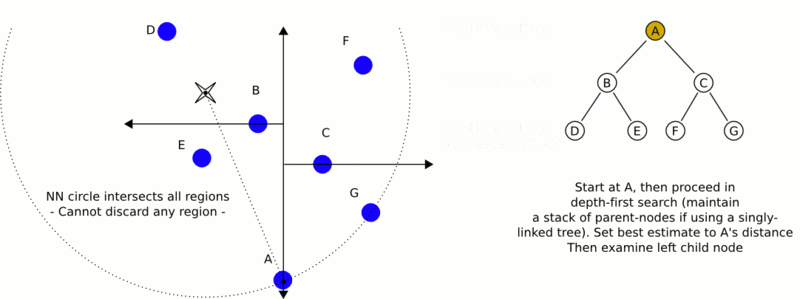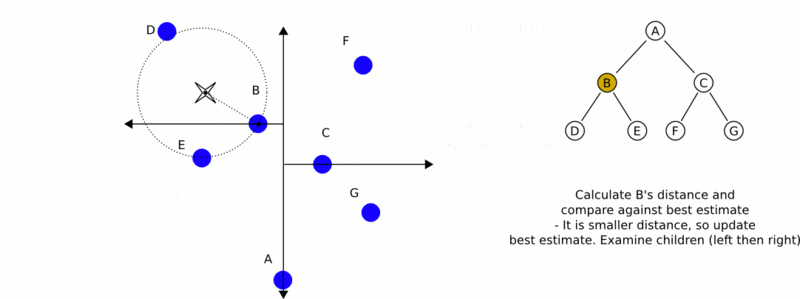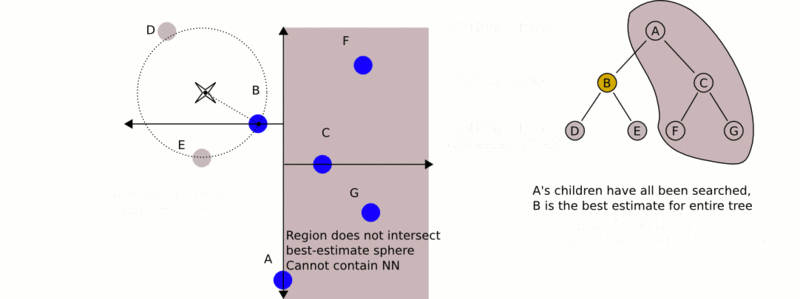
This is a demonstration of how nearest neighbor search works.

reference resources: https://pcl.readthedocs.io/projects/tutorials/en/latest/kdtree_search.html#kdtree-search

pclpy code

see kdTreeDemo.py

import pclpy
from pclpy import pcl
import numpy as np

if __name__ == '__main__':
    # Generate point cloud data
    cloud_size = 100
    a = np.random.ranf(cloud_size * 3).reshape(-1, 3) * 1024
    cloud = pcl.PointCloud.PointXYZ.from_array(a)

    kdtree = pcl.kdtree.KdTreeFLANN.PointXYZ()
    kdtree.setInputCloud(cloud)
    searchPoint = pcl.point_types.PointXYZ()
    searchPoint.x = np.random.ranf(1) * 1024
    searchPoint.y = np.random.ranf(1) * 1024
    searchPoint.z = np.random.ranf(1) * 1024
    # k nearest neighbor search
    k = 8
    pointIdxNKNSearch = pclpy.pcl.vectors.Int([0] * k)
    pointNKNSquaredDistance = pclpy.pcl.vectors.Float([0] * k)
    print('K nearest neighbor search at (', searchPoint.x,
          '', searchPoint.y,
          '', searchPoint.z,
          ') with k =', k, '\n')
    if kdtree.nearestKSearch(searchPoint, k, pointIdxNKNSearch, pointNKNSquaredDistance) > 0:
        for i in range(len(pointIdxNKNSearch)):
            print("  ", cloud.x[pointIdxNKNSearch[i]],
                  " ", cloud.y[pointIdxNKNSearch[i]],
                  " ", cloud.z[pointIdxNKNSearch[i]],
                  " (squared distance: ", pointNKNSquaredDistance[i], ")", "\n")

    # Use radius nearest neighbor search
    pointIdxNKNSearch = pclpy.pcl.vectors.Int()
    pointNKNSquaredDistance = pclpy.pcl.vectors.Float()

    radius = np.random.ranf(1) * 256.0
    print("Neighbors within radius search at (", searchPoint.x,
          " ", searchPoint.y, " ", searchPoint.z, ") with radius=",
          radius, '\n')
    if kdtree.radiusSearch(searchPoint, radius, pointIdxNKNSearch, pointNKNSquaredDistance) > 0:
        for i in range(len(pointIdxNKNSearch)):
            print("  ", cloud.x[pointIdxNKNSearch[i]],
                  " ", cloud.y[pointIdxNKNSearch[i]],
                  " ", cloud.z[pointIdxNKNSearch[i]],
                  " (squared distance: ", pointNKNSquaredDistance[i], ")", "\n")

explain

The following code first uses Numpy to create and populate the PointCloud with random data.

# Generate point cloud data
cloud_size = 100
a = np.random.ranf(cloud_size * 3).reshape(-1, 3) * 1024
cloud = pcl.PointCloud.PointXYZ.from_array(a)

The next code creates our kdtree object and sets the cloud we randomly created as input. Then we create a "searchPoint", which is assigned random coordinates.

kdtree = pcl.kdtree.KdTreeFLANN.PointXYZ()
kdtree.setInputCloud(cloud)
searchPoint = pcl.point_types.PointXYZ()
searchPoint.x = np.random.ranf(1) * 1024
searchPoint.y = np.random.ranf(1) * 1024
searchPoint.z = np.random.ranf(1) * 1024

Now we create an integer (and set it to 10) and two vectors to store the K nearest neighbors from the search.

k = 8
pointIdxNKNSearch = pclpy.pcl.vectors.Int([0] * k)
pointNKNSquaredDistance = pclpy.pcl.vectors.Float([0] * k)
print('K nearest neighbor search at (', searchPoint.x,
      '', searchPoint.y,
      '', searchPoint.z,
      ') with k =', k, '\n')

Suppose our KdTree returns more than 0 nearest neighbors, then it prints out the positions of all 10 nearest neighbors to our random "searchPoint", which have been stored in the vector we created earlier.

if kdtree.nearestKSearch(searchPoint, k, pointIdxNKNSearch, pointNKNSquaredDistance) > 0:
    for i in range(len(pointIdxNKNSearch)):
        print("  ", cloud.x[pointIdxNKNSearch[i]],
        " ", cloud.y[pointIdxNKNSearch[i]],
        " ", cloud.z[pointIdxNKNSearch[i]],
        " (squared distance: ", pointNKNSquaredDistance[i], ")", "\n")

Here is another demonstration of using radius nearest neighbor search to find all neighbors of a given "searchPoint" within a (randomly generated) radius. Two vectors are created again to store information about our neighbors.

# Use radius nearest neighbor search
pointIdxNKNSearch = pclpy.pcl.vectors.Int()
pointNKNSquaredDistance = pclpy.pcl.vectors.Float()

radius = np.random.ranf(1) * 256.0
print("Neighbors within radius search at (", searchPoint.x,
          " ", searchPoint.y, " ", searchPoint.z, ") with radius=",
          radius, '\n')

Similarly, as before, if our KdTree returns more than 0 neighbors within the specified radius, it will print the coordinates of these points, which have been stored in our vector.

if kdtree.radiusSearch(searchPoint, radius, pointIdxNKNSearch, pointNKNSquaredDistance) > 0:
        for i in range(len(pointIdxNKNSearch)):
            print("  ", cloud.x[pointIdxNKNSearch[i]],
                  " ", cloud.y[pointIdxNKNSearch[i]],
                  " ", cloud.z[pointIdxNKNSearch[i]],
                  " (squared distance: ", pointNKNSquaredDistance[i], ")", "\n")

function

Run kdTreeDemo.py

Operation results:

K nearest neighbor search at ( 737.6050415039062 750.3650512695312 411.2821960449219 ) with k = 8

753.9883 643.7369 456.1752 (squared distance: 13653.359375 )

828.60803 626.9191 501.09518 (squared distance: 31586.8125 )

760.72687 627.8939 539.5448 (squared distance: 31985.091796875 )

810.8796 972.1281 278.54584 (squared distance: 72166.953125 )

598.6487 507.64853 444.17035 (squared distance: 79301.8125 )

649.69885 946.6329 597.18005 (squared distance: 80806.5625 )

476.53268 646.1927 467.837 (squared distance: 82209.1015625 )

878.47424 922.55475 621.521 (squared distance: 93693.7734375 )

Neighbors within radius search at ( 737.6050415039062 750.3650512695312 411.2821960449219 ) with radius= [203.92877983]

753.9883 643.7369 456.1752 (squared distance: 13653.359375 )

828.60803 626.9191 501.09518 (squared distance: 31586.8125 )

760.72687 627.8939 539.5448 (squared distance: 31985.091796875 )

Note: because our data is generated with, the results are different every time. Sometimes, KdTree may return the nearest neighbor of 0, and there is no output at this time.