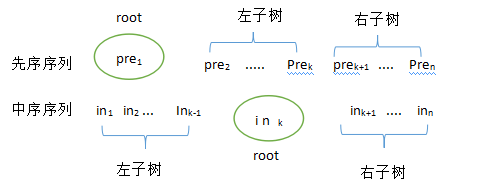
Suppose that the known sequence is pre1, pre2. pren, and the intermediate sequence is in1, in2. inn. As shown in the figure below, u is known by the nature of the sequence. The first element of the sequence is pre1, which is the root node of the current binary tree. Secondly, we can see that the root node of the current binary tree divides the intermediate sequence into left subtree and right subtree. So as long as we find a node ink in the ordered sequence, so that ink==pre1, we can find the root node. The number of nodes in a left subtree is numLeft=k-1, so the interval of the left subtree's precedence sequence is [2,k], the left subtree's middle sequence interval is [1,k-1], the right subtree's precedence sequence interval is [k+1,n], and the right subtree's middle sequence interval is [k+1,n].

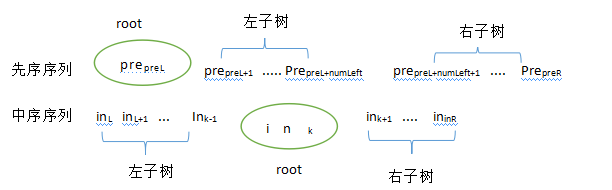
Generally speaking, if the interval of the current sequence is [preL,preR], the interval of the intermediate sequence is [inL,inR]. Then numLeft=k-inL is the number of nodes in the left subtree. In this way, the interval of the precedence sequence of the left subtree is [preL+1,preL+numLeft], the interval of the middle sequence of the left subtree is [inL,k-1], the interval of the precedence sequence of the right subtree is [preL+numLeft+1,preR], and the interval of the middle sequence of the right subtree is [k+1,inR]. Specific intervals can be seen in the following figure.

Each recursion can get the root node of the corresponding subtree, so where is the recursive boundary? Obviously, as long as the length of the sequence is less than or equal to zero, the binary tree does not exist.

For example, the given binary tree is shown in the following figure:

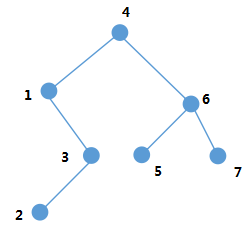
Preorder traversal: 41 3 2 6 5 7

Intermediate traversal: 1 23 4 5 6 7

Postorder traversal: 23 1 5 7 6 4

Hierarchical traversal: 41 6 3 5 7 2

Priority-Middle Order

The definition structure is as follows:

const int M=100; //Maximum number of nodes 
int pre[M],in[M],post[M],lay[M],;//Sequence subscripts for front, middle, back and hierarchical traversal start from 1 
int map[M];//Save the element subscripts of the hierarchical traversal sequence (elements are too large to be replaced by STL-map) 

struct Node{
	int data;
	Node *lchild ,*rchild;
}; 

Based on the above analysis, the following code is given to construct a binary tree from precedence and neutrality:

Node* create(int preL,int preR,int inL,int inR){  //Initial create(1,n,1,n)
	if(preL>preR){//Recursive boundary 
		return NULL;
	}
	Node* root=new Node();
	root->data=pre[preL];//Save the current root value 
	int k; //root is the subscript in the middle order 
	for(k=inL;k<=inR;k++){
		if(in[k]==pre[preL]){//Find root in intermediate order 
			break;
		} 
	}
	int numLeft=k-inL;//Get the number of left subtree nodes
	//Recursive construction of left subtree 
	root->lchild=create(preL+1,preL+numLeft,inL,k-1); 
	//Recursive construction of right subtree 
	root->rchild=create(preL+numLeft+1,preR,k+1,inR); 
	return root; 
}

Postorder-Intermediate Order

Binary trees are constructed from postorder and midorder. From the nature of post-order traversal, we can see that the last element is the root node, and the interval of the sequence has not changed. We only need to modify the preceding part of the above code. The modified code is as follows:

Node* createByPostInOrder(int postL,int postR,int inL,int inR){
	if(postL>postR){//Recursive boundary 
		return NULL;
	}
	Node* root=new Node();
	root->data=post[postR];//Save the current root value 
	int k; //root is the subscript in the middle order 
	for(k=inL;k<=inR;k++){
		if(in[k]==post[postR]){//Find root in intermediate order 
			break;
		} 
	}
	int numLeft=k-inL;//Get the number of left subtree nodes
	//Recursively construct left subtree and modify interval parts of subsequent order
	root->lchild=createByPostInOrder(postL,postL+numLeft-1,inL,k-1); 
	//Recursive construction of right subtree 
	root->rchild=createByPostInOrder(postL+numLeft,postR-1,k+1,inR); 
	return root; 
}

Hierarchy-Intermediate Order