woc, it's too difficult. It's just a fairy fighting. I don't have any confidence to continue when I see the number of people
All a, master's blog , then the environment was turned off at the moment of sending WP
Four questions, one in the backpack, one in the AGCD of RSA, one in AES.OCB, and the last unclear test point
WM
Crypto-checkin(recuring)
As we all know, L1near is a famous hacker. He wrote a fully automatic water swarm robot for W & M. we stole the simple version of L1near during development and obtained the interactive interface. Can you help us find the flag hidden by L1near?
The next day, update
Please submit the smallest of the Legal Secrets. The title is not clear, which has caused trouble to all masters
<title>W&M exclusive robot</title>
<style>
h1 {text-align:center}
p {text-align:center}
form {text-align:center}
</style>
<head>
<body>
<h1>Fully automatic rp system</h1>
<p>Come and get your rp value today!</p>
<hr></hr>
<form action="show.php" method="post">
<input type="hidden" id="rp" name="rp" value="rp">
<input type="submit" value="Get today's rp!">
</form>
</body>
</head>
<script>
function ran(){
var rp = Math.floor( Math.random() * 100);
document.getElementById("rp").setAttribute('value',rp);
}
ran();
</script>
<!--
-------------------------------------------------------
Maybe there are some Easter eggs?
So where are them?
-->
rp is an integer from 0 to 99, but post100 will get
<title>W&M exclusive robot</title>
<style>
h1 {text-align:center}
p {text-align:center}
</style>
<h1>Fully automatic rp system</h1>
<p>Come and get your rp value today!</p>
<hr></hr>
<p>Your rp value:100</p>
<p>Wow! Golden legend!<!-- so why not try to post 'flag' as rp? --></p>
I didn't analyze anything. I'll sort it out a little
-
0~19
Ah-ha! There is a idiot!
-
20~39
Gee, this is too miserable.
-
40~59
Oh, you almost passed it!
-
60~79
Fortunately, you passed 60.
-
80~99
You are Koi! Congratulations!
-
100
Wow! Golden legend!<!-- so why not try to post 'flag' as rp? -->
-
flag
Your rp value:1620418829165478 What happend to my bot????? Let me find something in my backpack which can fix this bug!
Write a post script for the first time and hold a memorial ceremony
from Crypto.Util.number import *
import requests
def exDigit(String):
d = 0
for j in String:
if '0' <= j <= '9':
d = d * 10 + int(j)
return d
x = 999999999999999999999999999999999
url = "http://47.104.243.99:10000/show.php"
r = requests.post(url, {"rp": 2017515922459700})
for i in range(65537):
if 'flag' in r.text or 'WMCTF' in r.text or 'wmctf' in r.text or '1620418829165478' in r.text:
print(r.text)
print(x)
line = r.text[205:][:37]
t = exDigit(line)
if t < x:
x = t
print(t)
payload = {
"rp": t
}
r = requests.post(url, payload)
However, after reading WP, I found that the information collected was useless. I directly exploded in situ
It's a backpack, This backpack on CTF Wiki is very easy to understand , master the following concepts: Super increment, Merkle Hellman knapsack encryption, and 01 lattice cracking
But I don't understand the series after reading WP. First, I want to know how to see that the knapsack is encrypted behind the machine, and then why post 2^i+a can get the value of each item of the knapsack. What are I and a respectively
The current understanding is that 1620418829165478 obtained by post flag is the ciphertext, and then the private key is cracked and decrypted
But there are still many doubts and incomprehensions. It's too difficult. Follow up
Here we are. This is the third reappearance in recent days. After reading master Striving's blog, I finally understand it more or less. Well, the chicken is my own
When I saw the backpack I thought of, I always thought it meant backup
A brief introduction to knapsack encryption is learned from la guy again
First of all, the knapsack problem is the knapsack problem we are familiar with. The following passage may be able to regain our memory

-
Private key generation
Select a super increment set { s 1 , s 2 , ⋯ , s n } \{s_1, s_2, \cdots, s_n\} {s1,s2,⋯,sn}
The so-called super increasing set is to satisfy that the i-th number is greater than the sum of all previous numbers
-
Public key generation
-
Select modulus m to ensure n > ∑ i = 1 n s i n>\sum\limits_{i=1}^n s_i n>i=1∑nsi
-
Select the multiplier w to ensure ( w , m ) = 1 (w,\ m)=1 (w, m)=1, where W is also the private key
-
Generate public key set t i t_i ti, t i ≡ w s i ( m o d m ) t_i\equiv ws_i\ (mod\ m) ti≡wsi (mod m)
-
-
encryption
The binary of each bit of plaintext b is b i b_i bi
c = ∑ i = 1 n t i b i ( m o d m ) c=\sum\limits_{i=1}^nt_ib_i\ (mod\ m) c=i=1∑ntibi (mod m) -
decrypt
Ask first w − 1 w^{-1} w − 1, then
b = ∑ i = 1 n w − 1 t i b i ( m o d m ) = ∑ i = 1 n s i b i ( m o d m ) b=\sum\limits_{i=1}^nw^{-1}t_ib_i\ (mod\ m)=\sum\limits_{i=1}^ns_ib_i\ (mod\ m) b=i=1∑nw−1tibi (mod m)=i=1∑nsibi (mod m)
The cryptosystem has a density of d = n l o g 2 ( m a x { t i } ) d=\frac{n}{log_2(max\{t_i\})} d=log2(max{ti})n
Then it's what I can't understand. Master Striving said that master Chunge said every post 2 i 2^i 2i, you will find that the period is 32, and the obtained value is the value in the public key set. Borrowing data is equivalent to knowing the public key set and ciphertext. Plaintext is required
t = [97005071980911, 32652300906411, 73356817713575, 108707065719744, 103728503304990, 49534310783118, 53330718889073, 2121345207564, 46184783396167, 115771983454147, 64261597617025, 2311575715655, 56368973049223, 84737125416797, 24316288533033, 82963866264519, 101019837363048, 25996629336722, 41785472478854, 68598110798404, 40392871001665, 94404798756171, 54290928637774, 112742212150946, 91051110026378, 124542182410773, 40388473698647, 22059564851978, 57353373067776, 80692115733908, 84559172686971, 28186390895657] c = 1620418829165478
With this, we can find the density
from math import log d = len(t) / log(max(t), 2) # d = 0.6834156494834176
It's said that low density can be done directly. I don't understand the principle. Copying a script also uses grid
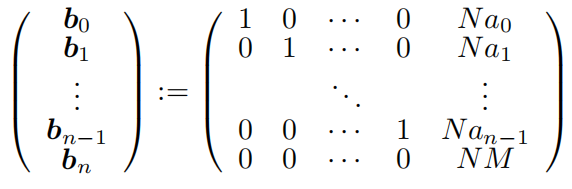
t = [97005071980911, 32652300906411, 73356817713575, 108707065719744, 103728503304990, 49534310783118, 53330718889073, 2121345207564, 46184783396167, 115771983454147, 64261597617025, 2311575715655, 56368973049223, 84737125416797, 24316288533033, 82963866264519, 101019837363048, 25996629336722, 41785472478854, 68598110798404, 40392871001665, 94404798756171, 54290928637774, 112742212150946, 91051110026378, 124542182410773, 40388473698647, 22059564851978, 57353373067776, 80692115733908, 84559172686971, 28186390895657]
c = 1620418829165478
n = len(t)
M = Matrix.identity(n)
last_row = [0 for x in t]
M_last_row = Matrix(ZZ, 1, len(last_row), last_row)
ct = 1620418829165478
last_col = t[:]
last_col.append(ct)
M_last_col = Matrix(ZZ, len(last_col), 1, last_col)
M = M.stack(M_last_row)
M = M.augment(M_last_col)
X = M.LLL()
target = X[-1][:-1]
ans = [abs(k) for k in target]
flag = int(''.join([str(i) for i in ans])[::-1], 2)
# 4159506287
Magic changed la guy's script
Then I heard that the string of numbers of the decrypted flag were post ed in the past to get the flag. Did you get it
Crypto-ocb(unsolved)
L1near is tired of the life of AK competition. He wants to take this opportunity to learn AES.OCB, which is his latest encryption system. Please help him see what the problem is.
from ocb.aes import AES # https://github.com/kravietz/pyOCB
from base64 import b64encode, b64decode
from Crypto.Util.number import *
from hashlib import sha256
from secret import flag
from ocb import OCB
import socketserver
import signal
import string
import random
import os
xor = lambda s1 , s2 : bytes([x1^x2 for x1,x2 in zip(s1,s2)])
def check(data):
try:
if(len(data) % 16 != 0):
return False
for i in range(data[-1]):
if(data[-1] != data[-1-i]):
return False
return True
except:
return False
def pad(data):
if check(data):
return data
padlen = 16 - len(data) % 16
return data + padlen * bytes([padlen])
def unpad(data):
if not check(data):
return data
return data[:-data[-1]]
BANNER =br'''
__ __ ___ __ __ ___
/\ \ __/\ \ /\_ \ /\ \__ /\ \__ /'___\
\ \ \/\ \ \ \ __\//\ \ ___ ___ ___ ___ __ \ \ ,_\ ___ __ __ __ ___ ___ ___\ \ ,_\/\ \__/
\ \ \ \ \ \ \ /'__`\\ \ \ /'___\ / __`\ /' __` __`\ /'__`\ \ \ \/ / __`\ /\ \/\ \/\ \ /' __` __`\ /'___\ \ \/\ \ ,__\
\ \ \_/ \_\ \/\ __/ \_\ \_/\ \__//\ \L\ \/\ \/\ \/\ \/\ __/ \ \ \_/\ \L\ \ \ \ \_/ \_/ \/\ \/\ \/\ \/\ \__/\ \ \_\ \ \_/
\ `\___x___/\ \____\/\____\ \____\ \____/\ \_\ \_\ \_\ \____\ \ \__\ \____/ \ \___x___/'\ \_\ \_\ \_\ \____\\ \__\\ \_\
'\/__//__/ \/____/\/____/\/____/\/___/ \/_/\/_/\/_/\/____/ \/__/\/___/ \/__//__/ \/_/\/_/\/_/\/____/ \/__/ \/_/
'''
MENU = br'''[+] 1.Encrypt
[+] 2.Decrypt
[+] 3.Get flag
[+] 4.Exit
'''
class Task(socketserver.BaseRequestHandler):
def _recvall(self):
BUFF_SIZE = 2048
data = b''
while True:
part = self.request.recv(BUFF_SIZE)
data += part
if len(part) < BUFF_SIZE:
break
return data.strip()
def send(self, msg, newline=True):
try:
if newline:
msg += b'\n'
self.request.sendall(msg)
except:
pass
def recv(self, prompt=b'[-] '):
self.send(prompt, newline=False)
return self._recvall()
def proof_of_work(self):
random.seed(os.urandom(8))
proof = ''.join([random.choice(string.ascii_letters+string.digits) for _ in range(20)])
_hexdigest = sha256(proof.encode()).hexdigest()
self.send(f"[+] sha256(XXXX+{proof[4:]}) == {_hexdigest}".encode())
x = self.recv(prompt=b'[+] Plz tell me XXXX: ')
if len(x) != 4 or sha256(x+proof[4:].encode()).hexdigest() != _hexdigest:
return False
return True
def encrypt(self, nonce, message, associate_data=b''):
assert nonce not in self.NONCEs
self.NONCEs.append(nonce)
self.ocb.setNonce(nonce)
message = pad(message)
tag, cipher = self.ocb.encrypt(bytearray(message), bytearray(associate_data))
return (bytes(cipher), bytes(tag))
def decrypt(self, nonce, cipher, tag, associate_data=b''):
self.ocb.setNonce(nonce)
authenticated, message = self.ocb.decrypt(*map(bytearray, (associate_data, cipher, tag)))
message = unpad(message)
if not authenticated:
self.send(b"[!] Who are you???")
return b''
return message
def handle(self):
signal.alarm(60)
self.send(BANNER)
if not self.proof_of_work():
self.send(b'[!] Wrong!')
return
self.send(b'[+] Welcome my friend!')
self.send(b'[+] Can you find the secret through the easy encryption system?')
aes = AES(128)
self.ocb = OCB(aes)
KEY = os.urandom(16)
self.ocb.setKey(KEY)
self.NONCEs = []
while True:
self.send(MENU, newline=False)
choice = self.recv()
if(choice == b'1'):
try:
self.send(b'[+] Please input your nonce')
nonce = b64decode(self.recv())
self.send(b'[+] Please input your message')
message = b64decode(self.recv())
associate_data = b'from baby'
ciphertext, tag = self.encrypt(nonce, message, associate_data)
self.send(b"[+] ciphertext: " + b64encode(ciphertext))
self.send(b"[+] tag: " + b64encode(tag))
except:
self.send(b"[!] ERROR!")
elif(choice == b'2'):
try:
self.send(b'[+] Please input your nonce')
nonce = b64decode(self.recv())
self.send(b'[+] Please input your ciphertext')
ciphertext = b64decode(self.recv())
self.send(b'[+] Please input your tag')
tag = b64decode(self.recv())
self.send(b'[+] Please input your associate data')
associate_data = b64decode(self.recv())
if associate_data == b'from admin':
self.send(b'[!] You are not admin!')
break
message = self.decrypt(nonce, ciphertext, tag, associate_data)
self.send(b'[+] plaintext: ' + b64encode(message))
except:
self.send(b"[!] ERROR!")
elif(choice == b'3'):
try:
nonce = b'\x00'*16
message = flag
associate_data = b'from admin'
ciphertext, tag = self.encrypt(nonce, message, associate_data)
self.send(b"[+] ciphertext: " + b64encode(ciphertext))
self.send(b"[+] tag: " + b64encode(tag))
except:
self.send(b"[!] ERROR!")
elif(choice == b'4'):
self.send(b'[+] Bye~')
self.send(b'[+] See you next time!')
break
else:
self.send(b'[!] What are you doing???')
self.send(b'[!] Go away!')
break
self.request.close()
class ThreadedServer(socketserver.ThreadingMixIn, socketserver.TCPServer):
pass
class ForkedServer(socketserver.ForkingMixIn, socketserver.TCPServer):
pass
if __name__ == "__main__":
HOST, PORT = '0.0.0.0', 10001
server = ForkedServer((HOST, PORT), Task)
server.allow_reuse_address = True
print(HOST, PORT)
server.serve_forever()
Jinmen cup and hongminggu have similar problems. AES in ocb mode provides authentication. The process in this mode has not been studied carefully. Looking at the code, there is no way to bypass the associate_data == b'from admin'
Crypto-easylsb(recuring)
#!/usr/bin/python3
# encoding: utf-8
import random
import string
import sys
import os
from hashlib import sha256
import uuid
from Crypto.Util.number import *
password = # Hidden
flag = ('flag{' + str(uuid.uuid4()) + '}').encode()
def proof_of_work():
random.seed(os.urandom(8))
proof = ''.join([random.choice(string.ascii_letters+string.digits) for _ in range(20)]).encode()
digest = sha256(proof).hexdigest()
printf("sha256(XXXX+%s) == %s" % (proof[4:].decode(),digest))
printf('Give me XXXX:')
x = read_str()
if len(x) != 4 or sha256(x.encode()+proof[4:]).hexdigest() != digest:
return False
return True
def printf(message):
sys.stdout.write('{0}\n'.format(message))
sys.stdout.flush()
sys.stderr.flush()
def read_str():
return sys.stdin.readline().strip()
def read_int():
return int(sys.stdin.readline().strip())
def next_prime(a):
while not isPrime(a):
a += 2
return a
def get_prime(a):
suffix = getPrime(368)
return next_prime(a ** 2 + suffix + 1)
def generate_pubkey(key):
p, q = get_prime(getPrime(512)), get_prime(key)
n = p * q
return n
def airdrop(a):
n = generate_pubkey(a)
printf('gift: {}'.format(n))
return
def hint(n, e, c):
printf('n = {}'.format(n))
printf('e = {}'.format(e))
printf('c = {}'.format(c))
return
def leak():
p = get_prime(getPrime(512))
e = 0x1000
c = pow(bytes_to_long(flag), e, p)
hint(p, e, c)
return
def backdoor():
printf('Input your password:')
user_input = read_str()
if user_input.encode() == password:
leak()
else:
printf('Wrong')
exit(0)
if __name__ == '__main__':
if not proof_of_work():
exit(0)
a = getPrime(512)
p = get_prime(a)
q = get_prime(getPrime(512))
n = p * q
e = 0x10001
max_time = 5
password_enc = pow(bytes_to_long(password), e, n)
printf('====================================',)
printf('1. Airdrop ',)
printf('2. Backdoor ',)
printf('3. Hint ',)
printf('4. Exit ',)
printf('====================================',)
try:
while True:
printf('Your choice:')
choice = read_int()
if choice == 1:
if max_time > 1:
airdrop(a)
max_time -= 1
printf('Done!')
else:
printf('Greed will destroy you!')
continue
elif choice == 2:
backdoor()
printf('Done!')
continue
elif choice == 3:
hint(n, e, password_enc)
printf('Done!')
continue
elif choice == 4:
printf('bye~')
exit(0)
continue
else:
printf('Invalid!')
continue
except:
exit(-1)
The process is relatively simple. Although not, the idea is relatively clear. a and p are obtained through 4 groups of gift s and 1 n → \rightarrow → decrypt password → \rightarrow → decrypt the flag when e=4096 and the modulus is prime
At the beginning, master Shang reminded me that after trying, I found that the rounding result of q after root opening is the same as that of a
⌊
q
⌋
=
a
\lfloor \sqrt{q} \rfloor=a
⌊q
⌋=a
Then assume
q
=
n
e
x
t
_
p
r
i
m
e
(
a
2
+
s
u
f
f
i
x
1
+
1
)
,
p
=
n
e
x
t
_
p
r
i
m
e
(
b
2
+
s
u
f
f
i
x
2
+
1
)
q=next\_prime(a^2+suffix_1+1),\ p=next\_prime(b^2+suffix_2+1)
q=next_prime(a2+suffix1+1), p=next_prime(b2+suffix2+1)
So n=pq, you can get the high position of ab by giving n a root, but you don't know how to use it
Save a set of data and have a chance to study in the future
# nc 47.104.243.99 9999
import random
import string
import sys
import os
from hashlib import sha256
import uuid
from Crypto.Util.number import *
from pwn import *
from itertools import product
# flag = ('flag{' + str(uuid.uuid4()) + '}').encode()
# print(flag)
# flag{cb8365b5-a825-4c65-9251-b6827f0792ad}
def proof_of_work():
# sha256(XXXX+cgDUNjezTPNSj91D) == 30fc93b19ef81e8755f3ee0e3df72722f66556b7636b5037f34d1beb981235b0
proof = sh.recvline()
tail = proof[12:28].decode()
HASH = proof[23:97]
for i in product(string.ascii_letters + string.digits, repeat=4):
head = ''.join(i)
t = hashlib.sha256((head + tail).encode()).hexdigest()
if t == HASH:
sh.sendline(head.encode())
break
def proof_of_work2():
# sha256(XXXX+cgDUNjezTPNSj91D) == 30fc93b19ef81e8755f3ee0e3df72722f66556b7636b5037f34d1beb981235b0
proof = sh.recvline()
tail = 'eqbj8j6Z9xvz3YiV'
HASH = 'b5808aff39327c9ac49d209d10fe3e27c898d49faffc956bbf1d73523c44ce77'
for i in product(string.ascii_letters + string.digits, repeat=4):
head = ''.join(i)
t = hashlib.sha256((head + tail).encode()).hexdigest()
if t == HASH:
sh.sendline(head.encode())
break
context.log_level = 'debug'
sh = remote("47.104.243.99", 9999)
proof_of_work2()
e = 0x10001
n = 124478026101165354098037876421627662624056206605515177686194103211430464934743129994417330643128683345849733014275487857184516763016301408033382676283620282332485581507315430690690813831282519976585364463744017296315372258981215919387679949709396064987889800074036410663927631478105899096723790945928412829187822284593750473740315866322998068351563015099367643886154042581191841533888375305195743073059105310700318861167337672659772641786687582718180589854118978820530842381081568922213227168617789474006973152602334271699398178963791154954792676067153150646411025449463253194489657095241613282942586704728903727611399
c = 90647155870804971113806442051901226002120015769259333554192477899450971338831255790857101662710560234954831825416787459228033373486077151217415092360097814474283515220281223555587026056325099266316005605716929634353603643319859645167427538563242884591102004934790399528462112789803351851769047685792159647390050985871679243422993775721776244067168064933786611606433105514418429089777322132633028815660525070271128628044386434106685643657668695364607215033856398608992051550288297119711825866170869469834444973857013360900452988222767960318998636640763573797297203544581343736625672669946528644260077687270041162148579
gift1 = 430643544402084432319325961880416327356872029175895120742910502784460696485981655831364057771978842374920289740546998744096646780935886278222230684528731470188637076148307527311922452490801045278988434801896164340653915198079023711297016090027381126073802620204314765869166624636941907534206046998568042400815444697126334029985946496452932477337335924863188276040631646131204436116708742280199903183210826719901897273260766069768314579353548171372586771188839003301749872795307598319516051259672117483195538538878148292313730887085591272354625175614366936749367007177827223031514498275753340915542939818624965339274541
gift2 = 279643881521430665779764628210196159031443254319916096260435206316116655701344325784134050728686231352816394212502789612947929220430466611004330150352137570405484127780364316335386736272544877793446702006665399064591475517610575894857804921152265901610537191780251376268112843688812459951190257679817490601282013470378644045696567456486059374094892490322848884260103728441765221196492288890565220765116737467020984854284776188063793107604665880577892150257025900438921323929874583349697921571156857890185078774883450481945134786456867498237937223992977125106207044050316201931335150865420643200300919950666792333800421
gift3 = 237902069859826089956710602458488697197969935460375469157966706791637991891038954423106099106663742928616105443683571279895168734280020803510641968762322744746722455831059684745613465616901995570874116303439549541932451281441959514629564655972962203744852006794160278105621063202850402448076034174743227230202591123961117876362833492478366233652816443873213201410433457033307944305406209168085355438156499669719905462067847881209129983251184647052314353242784174374088582263983943733709287614092898665984536781786084591414804290805713181580225096207601673326693693442261927044483426965621699507399608913104482509541829
gift4 = 131184496439376311814751172869309509301398236134030748081290782986296909958428702969677021306310259793511587606469385852829507392096577310273567455635233040499932518933927338330158300947934921792366825549482737059128276134653805578959896357503546949681198843822945160611138388841031519307824760189249466171835761078895545203381195921789823129815826662876576368032722825159838976137103324588326186884693453137115752294499574361951327089081432442184727065530788376603390307277709197418051468405219378610308912749832078805547917787498228816440083434077213552664217150489211767711038795362880479839885325109115335568243823
Now you can reproduce the problem
First, supplement, get a, then we can see from the above conclusion a 2 a^2 a2 is the high position of q, isn't this the high position attack of p known by RSA
I don't know which equation system gets the lattice in WP
Well, the third wave reappears. I thought the agcd was the master's wrong number. It turned out to be my dish. It's a paper Approximate GCD

Look, the format and title correspond exactly
Ha ha, I can't understand it. Take ge and run away

x i x_i xi , obviously five groups n i n_i ni , the root sign is obtained, which is also confirmed above; λ \lambda λ It's 368, because in the paper r i r_i ri , is in the title s u f f i x i + 1 suffix_i+1 suffixi+1
In this way, LLL() is performed on matrix B to obtain q 0 ⋅ 2 λ + 1 q_0\cdot 2^{\lambda +1} q0⋅2 λ+ 1, divided by 2 λ + 1 2^{\lambda +1} two λ+ 1 is in the paper q 0 q_0 q0 , that is, with x 0 x_0 x0 , the corresponding one
So far, there is still one step missing, and then in the topic
n
=
p
q
n=pq
n=pq derivation
n
=
p
q
=
(
a
2
+
s
u
f
f
i
x
1
+
1
)
(
b
2
+
s
u
f
f
i
x
2
+
1
)
n=pq=(a^2+suffix_1+1)(b^2+suffix_2+1)
n=pq=(a2+suffix1+1)(b2+suffix2+1)
set up
β
=
b
2
+
s
u
f
f
i
x
2
+
1
,
δ
\beta =\sqrt {b^2+suffix_2+1},\ \delta
β=b2+suffix2+1
, δ Is the low position after p root opening,
r
=
δ
β
r=\delta \beta
r=δβ
Root n
n
=
(
a
+
δ
)
β
=
a
β
+
r
\sqrt n=(a+\delta)\beta =a\beta +r
n
=(a+δ)β=aβ+r
This is the same as the form given in the paper, and we just figured it out
q
0
q_0
q0# is here
β
\beta
β, last
⌊
n
/
β
⌋
=
⌊
(
a
β
+
r
)
/
β
⌋
\lfloor\sqrt n/\beta \rfloor =\lfloor (a\beta +r)/\beta\rfloor
⌊n
/ β ⌋=⌊(a β+ r)/ β ⌋, obviously
r
/
β
r/\beta
r/ β It's already a decimal part, and rounding is completely rounded off, so the result is a
The ans obtained should be b above. First use the master's script to get a
from sympy import root e = 0x10001 n = 124478026101165354098037876421627662624056206605515177686194103211430464934743129994417330643128683345849733014275487857184516763016301408033382676283620282332485581507315430690690813831282519976585364463744017296315372258981215919387679949709396064987889800074036410663927631478105899096723790945928412829187822284593750473740315866322998068351563015099367643886154042581191841533888375305195743073059105310700318861167337672659772641786687582718180589854118978820530842381081568922213227168617789474006973152602334271699398178963791154954792676067153150646411025449463253194489657095241613282942586704728903727611399 c = 90647155870804971113806442051901226002120015769259333554192477899450971338831255790857101662710560234954831825416787459228033373486077151217415092360097814474283515220281223555587026056325099266316005605716929634353603643319859645167427538563242884591102004934790399528462112789803351851769047685792159647390050985871679243422993775721776244067168064933786611606433105514418429089777322132633028815660525070271128628044386434106685643657668695364607215033856398608992051550288297119711825866170869469834444973857013360900452988222767960318998636640763573797297203544581343736625672669946528644260077687270041162148579 gift1 = 430643544402084432319325961880416327356872029175895120742910502784460696485981655831364057771978842374920289740546998744096646780935886278222230684528731470188637076148307527311922452490801045278988434801896164340653915198079023711297016090027381126073802620204314765869166624636941907534206046998568042400815444697126334029985946496452932477337335924863188276040631646131204436116708742280199903183210826719901897273260766069768314579353548171372586771188839003301749872795307598319516051259672117483195538538878148292313730887085591272354625175614366936749367007177827223031514498275753340915542939818624965339274541 gift2 = 279643881521430665779764628210196159031443254319916096260435206316116655701344325784134050728686231352816394212502789612947929220430466611004330150352137570405484127780364316335386736272544877793446702006665399064591475517610575894857804921152265901610537191780251376268112843688812459951190257679817490601282013470378644045696567456486059374094892490322848884260103728441765221196492288890565220765116737467020984854284776188063793107604665880577892150257025900438921323929874583349697921571156857890185078774883450481945134786456867498237937223992977125106207044050316201931335150865420643200300919950666792333800421 gift3 = 237902069859826089956710602458488697197969935460375469157966706791637991891038954423106099106663742928616105443683571279895168734280020803510641968762322744746722455831059684745613465616901995570874116303439549541932451281441959514629564655972962203744852006794160278105621063202850402448076034174743227230202591123961117876362833492478366233652816443873213201410433457033307944305406209168085355438156499669719905462067847881209129983251184647052314353242784174374088582263983943733709287614092898665984536781786084591414804290805713181580225096207601673326693693442261927044483426965621699507399608913104482509541829 gift4 = 131184496439376311814751172869309509301398236134030748081290782986296909958428702969677021306310259793511587606469385852829507392096577310273567455635233040499932518933927338330158300947934921792366825549482737059128276134653805578959896357503546949681198843822945160611138388841031519307824760189249466171835761078895545203381195921789823129815826662876576368032722825159838976137103324588326186884693453137115752294499574361951327089081432442184727065530788376603390307277709197418051468405219378610308912749832078805547917787498228816440083434077213552664217150489211767711038795362880479839885325109115335568243823 f = lambda a: int(root(a, 2)) x0, x1, x2, x3, x4 = f(n), f(gift1), f(gift2), f(gift3), f(gift4) B = matrix(ZZ, [[2 ^ 368, x1, x2, x3, x4], [0, -x0, 0, 0, 0], [0, 0, -x0, 0, 0], [0, 0, 0, -x0, 0], [0, 0, 0, 0, -x0]]) L = B.LLL() ans = L[0][0] // 2 ^ 368 p0 = abs(ans) a = x0 // p0 print(a) # a = 25582847577564670038612582668140373129129959651036453923605273284793860890291221263498753328353767798264241675861426056503889321642277844202986695039010291
Then there is the familiar rhythm, but it is different from the general known p high-level attack a 2 a^2 a2 is almost the same as the number of bits of p, but I don't know how much the suffix of 368 bits is, so the essence is the same. Use the CopperSmith algorithm to find the suffix; The kbits here is 369, because 368 can't get out. Go to a larger place
a = 25582847577564670038612582668140373129129959651036453923605273284793860890291221263498753328353767798264241675861426056503889321642277844202986695039010291 n = 124478026101165354098037876421627662624056206605515177686194103211430464934743129994417330643128683345849733014275487857184516763016301408033382676283620282332485581507315430690690813831282519976585364463744017296315372258981215919387679949709396064987889800074036410663927631478105899096723790945928412829187822284593750473740315866322998068351563015099367643886154042581191841533888375305195743073059105310700318861167337672659772641786687582718180589854118978820530842381081568922213227168617789474006973152602334271699398178963791154954792676067153150646411025449463253194489657095241613282942586704728903727611399 pbar = a ** 2 kbits = 369 PR.<x> = PolynomialRing(Zmod(n)) f = pbar + x roots = f.small_roots(X=2^kbits, beta=0.4) # 967901962469872165537856438801710756065070673694594801499396171114255660549746759504438698205658088002955084386
Next, the regular steps of RSA get the password
Cou1d_I_get_Th3_passw03d_then_captu7e_the_fla9?
Because I didn't get the c of flag in the competition, I borrowed it from this master
As I said at the beginning, is e even or 2 12 2^{12} 212, and φ ( p ) = p − 1 \varphi(p)=p-1 φ( p)=p − 1 is not mutually prime. You should say PUTAOAO at this time. Your line is wrong. You can't say heaven or anything when you take revenge. It should be like this: my name is master Shang. In order to calm the regret and hatred of my friend 4XWi11 and let the spirit of my left friend Y1m0 rest in heaven, I need you to 4 apologize!

Square root, square root of finite field, Rabin, a shuttle
However, considering that 4096 here is relatively large, the square of finite field will be very slow. Use nthroot directly_ The mod function doesn't seem to work. The traditional rabin function doesn't work because the modulus is p; Seeing the master's enlightenment, I specially sent an article about rabin principle blog
Although I don't know nthroot_ Why not mod? Because P% 4 = 3 meets the most basic condition of rabin, it is necessary to meet this condition, and this condition is the condition with few results, so there is no pressure to directly open the 12th power
The key codes m1 = pow(c, (p + 1) // 4, p) and m2 = p - m1
from Crypto.Util.number import long_to_bytes
p = 496584754781581997154645314415051021632937719346451955222548277806458479939882609131615548616817732786901123585586203791585231652481101508165523306207307511005218236201069837205145881515297396218450658339325435517394532697652694250302927324547950654199907918057947165277944713164863611463887879016367147027651
e = 4096
c = 202821697585498721190880385651888326819052363235092021514522019296117832067188656931773131985516119359273814956340533509702817980744398402155886334655033938474295749168241550740096583920405311629354495691732306096266636370938656838375279086916114964255411601403125984312042419408682006688199111243135798564394
mi = []
for i in range(12):
mi.append(pow(c, (p + 1) // 4, p))
mi.append(p - pow(c, (p + 1) // 4, p))
c = pow(c, (p + 1) // 4, p)
for i in mi:
t = long_to_bytes(i)
if b'WMCTF' in t:
print(t)
break
Then it seems that Striving's blog is also available in the limited field. It seems that I didn't understand the essence. ctfshow unusualrsa series blog In fact, with sage, everything is not complicated
from Crypto.Util.number import * p = 496584754781581997154645314415051021632937719346451955222548277806458479939882609131615548616817732786901123585586203791585231652481101508165523306207307511005218236201069837205145881515297396218450658339325435517394532697652694250302927324547950654199907918057947165277944713164863611463887879016367147027651 e = 4096 c = 202821697585498721190880385651888326819052363235092021514522019296117832067188656931773131985516119359273814956340533509702817980744398402155886334655033938474295749168241550740096583920405311629354495691732306096266636370938656838375279086916114964255411601403125984312042419408682006688199111243135798564394 R.<x> = Zmod(p)[] f = x ^ e - c f = f.monic() res1 = f.roots() print(res1) # res1 = [(496584754781581997154645314415051021632937719346451955222548277806458479939882609131615548616817732786901123585586203791585231652481101508165523306207307511005218236201069837205145881515297396218450658339313214656968189495352306293673615992017103882095004555948437432049586089024300970437646867574391499674950, 1), (12220860426343202300387956629311332530846772104903362109509733228358624140562641026241011441975647352701, 1)] c = 12220860426343202300387956629311332530846772104903362109509733228358624140562641026241011441975647352701 print(long_to_bytes(c))
It's true. It runs faster than expected
Crypto-ezl1near(unsolved)
from Crypto.Util.number import long_to_bytes , bytes_to_long , getPrime , inverse
from Crypto.Cipher import AES
import socketserver , signal
import random
import string
from hashlib import sha256
import os
from secret import flag
q = 2**24
def getrandbits(n):
return bytes_to_long(os.urandom(n // 8+1)) >> (8-n%8)
class server(socketserver.BaseRequestHandler):
def _recv(self):
data = self.request.recv(1024)
return data.strip()
def _send(self, msg, newline=True):
if isinstance(msg , bytes):
msg += b'\n'
else:
msg += '\n'
msg = msg.encode()
self.request.sendall(msg)
def proof_of_work(self):
random.seed(os.urandom(8))
proof = ''.join([random.choice(string.ascii_letters+string.digits) for _ in range(20)])
_hexdigest = sha256(proof.encode()).hexdigest()
self._send(f"sha256(XXXX+{proof[4:]}) == {_hexdigest}".encode())
self._send(b'Give me XXXX: ')
x = self._recv()
if len(x) != 4 or sha256(x+proof[4:].encode()).hexdigest() != _hexdigest:
self.send('wrong')
return False
return True
def genrsa(self):
_p = getPrime(1024)
_q = getPrime(1024)
self.n = _p * _q
self.e = 65537
self.d = inverse(self.e , (_p-1)*(_q-1))
def to_vec(self,num , length):
vec = []
while length > 0:
vec = [num % q] + vec
num //= q
length -= 1
return vec
def to_mat(self,numlist):
M =[]
for i in numlist:
M.append(self.to_vec(i , 40))
return M
def enc(self, key , m):
key = self.to_mat(key)
res = []
for i in range(40):
temp = 0
for j in range(16):
temp += m[j]* key[j][i]
temp %= q
res.append(temp)
return res
def handle(self):
signal.alarm(120)
self.proof_of_work()
self.genrsa()
self._send(str(self.n))
self._send(str(self.e))
secret = [1] + [2*getrandbits(23)-1 for _ in range(15)]
self._send(b'Please generate key for me and I will give you my secret.But you have only two chances.')
for i in range(2):
key = []
f0 = getrandbits(480)
key.append(f0)
self._send(str(pow(f0 , self.e , self.n)))
f0 += f0 << 480
for j in range(15):
self._send('key'+str(i+1) + ':')
c = int(self._recv())
m = pow(c , self.d , self.n)
f = m - f0
f %= self.n
key.append(f)
c = self.enc(key , secret)
self._send('Thanks, here is your cipher:' + str(c))
self._send(b'do you know the secret?')
guess = [int(i) for i in self._recv().split(b' ')]
if len(guess) == 16:
for j in range(16):
if guess[j] != secret[j]:
break
else:
self._send(b'congratulations. here is your flag:')
self._send(flag)
return 0
else:
self._send(b'L1near don\'t care.')
class ForkedServer(socketserver.ForkingMixIn, socketserver.TCPServer):
pass
if __name__ == "__main__":
HOST, PORT = '0.0.0.0', 10000
server = ForkedServer((HOST, PORT), server)
server.allow_reuse_address = True
server.serve_forever()
I'm not in the mood. I can't watch it anymore
It can be said to be a major mistake. The password burst 0 in the whole process. I'm sorry for the master of web and misc