Catalog
Random inversion matrix
describe
You are given a binary matrix of m x n, and all values are initialized to zero. Please design an algorithm to randomly select one that satisfies Subscript of matrix[i][j] == 0 (i, j) and change its value to 1. The probability that all subscripts (i, j) satisfying matrix[i][j] == 0 will be selected should be equal.
Minimize calls to built-in random functions and optimize time and space complexity.
Implement the Solution class:
- Solution(int m, int n): Initialize the object using the size M and N of the binary matrix
- int[] flip(): returns a satisfying matrix[i][j] == 0 random subscript [i, j], and change the value in its corresponding grid to 1
- void reset(): Resets all values in the matrix to zero
Example
input ["Solution", "flip", "flip", "flip", "reset", "flip"] [[3, 1], [], [], [], [], []] output [null, [1, 0], [2, 0], [0, 0], null, [2, 0]] explain Solution solution = new Solution(3, 1); solution.flip(); // Return [1,0], where the probability of returning [0,0], [1,0] and [2,0] should be the same solution.flip(); // Return [2,0] because [1,0] has already been returned and the probability of returning [2,0] and [0,0] should be the same solution.flip(); // Returns [0,0], which can only be returned at this time based on subscripts that have been previously returned solution.reset(); // All values are reset to 0, and subscript returns can be selected again solution.flip(); // Return [2,0], where the probability of returning [0,0], [1,0] and [2,0] should be the same
Tips
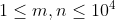
- At least one grid with a value of 0 exists in the matrix each time flip is called.
- Up to 1000 flip and reset method calls
Method: Array Mapping
We can consider converting a matrix to a length of M × The one-dimensional array map of n, for locations (i, j) i n the matrix, corresponds to the element map[i * n + j] i n the map, thus ensuring the element mapping of the matrix and map. After M × After flip n_k times, we will modify the map mapping to the matrix so that there is m in the current matrix × N_k 1 and K 00.
In this case, we use the exchange of elements in the array to make the map[0_ k - 1] maps to 0 in the matrix, and map[k] _m × n - 1] maps to 1 in the matrix. The advantage is that when we do the next flip, we only need to generate a random number x in this interval [0, k-1] and flip the position of the matrix to which the map[x] is mapped.
After flipping the map[x], there is k_1 0 in the matrix, so we need to ensure that the map [0.. K - 2] is mapped to 0 in the matrix. Since map[x] is now mapped to 1 in the matrix, we can swap the value of map[x] with that of map [k-1], that is, the newly flipped 1 is mapped to map [k-1], and the 0 mapped to map [k-1] is given to X. This ensures that after each flip, the map The first k elements in the matrix map exactly to all k zeros in the matrix.
So how do we maintain this one-dimensional array map? We can see that most of the mapping relationships I n a map do not change, that is, the (i, j) i n the matrix is mapped to A[i * n + j], so we can use a HashMap to store those maps that have been modified. For a number x, if x is not a key in HashMap, it maps directly to the beginning (x/n, x%n); If x is a key in HashMap, it maps to its corresponding value in HashMap. The actual size of the HashMap in operation is only proportional to the number of flips, because for each flip we exchange the mapping of two elements in the map, that is, the mapping relationship of up to two elements is modified.
class Solution {
Map<Integer, Integer> map = new HashMap<>();
int m, n, total;
Random rand = new Random();
public Solution(int m, int n) {
this.m = m;
this.n = n;
this.total = m * n;
}
public int[] flip() {
int x = rand.nextInt(total);
total--;
// Find mappings for location x
int idx = map.getOrDefault(x, x);
// Set the mapping for location x to the mapping for location total
map.put(x, map.getOrDefault(total, total));
return new int[]{idx / n, idx % n};
}
public void reset() {
total = m * n;
map.clear();
}
}