Write before

This article uses python as the programming language and the author practices it by himself. The list of topics is: Swordfinger Offer (2nd Edition) ""Swordfinger Offer (2nd Edition)"passes through the world's classic secrets for programmer interviews. Analyse typical programming interviews, collate the basic knowledge, code quality, solution ideas, optimization efficiency and comprehensive competence of the five interview points."In this paper, the ideas come from the problem section in each topic, and strive to provide a comprehensive, optimized solution, in which all the code has passed the topic test.

Swordfinger Offer 37.Serialize Binary Tree (Difficult)

subject

thinking

• Serialization: Hierarchical traversal, then revert back. Hierarchical traversal is bfs. Note that when nulls are encountered, append("null") is not added anymore. And "serialization" means "become a string", so don't use node.val directly. The final return must also be a string!
• Deserialization: Empty nodes are skipped by hierarchy, and non-empty nodes are left and right. Queues are still needed here. Nodes that have been added to the left and right subtrees need to be added to the queue to facilitate the addition of lower layers.

Problem

• BFS hierarchical traversal:

class Codec:
    def serialize(self, root):
        if not root: return "[]"
        queue = []
        queue.append(root)
        res = []
        while queue:
            node = queue.pop(0)
            if node:
                res.append(str(node.val))
                queue.append(node.left)
                queue.append(node.right)
            else: res.append("null")
        return '[' + ','.join(res) + ']'
        
    def deserialize(self, data):
        if data == "[]": return
        nodes = data[1:-1].split(',')
        root = TreeNode(int(nodes[0]))
        queue = []
        queue.append(root)
        i = 1
        while queue:
            node = queue.pop(0)
            if nodes[i] != "null":
                node.left = TreeNode(int(nodes[i]))
                queue.append(node.left)
            i += 1
            if nodes[i] != "null":
                node.right = TreeNode(int(nodes[i]))
                queue.append(node.right)
            i += 1
        return root
        

• DFS traversal (because there is no standard for serialization, it can be serialized in any way, and the meaning of DFS here is to show how to complete the deserialization recursively):

class Codec:
    def serialize(self, root):
        if not root:
            return 'None'
        return str(root.val) + ',' + str(self.serialize(root.left)) + ',' + str(self.serialize(root.right))
        
    def deserialize(self, data):
        def dfs(nodes):
            val = nodes.pop(0)
            if val == 'None':
                return None
            root = TreeNode(int(val))
            root.left = dfs(nodes)
            root.right = dfs(nodes)
            return root

        nodes= data.split(',')
        return dfs(nodes)

Sword Finger Offer 38.Arrangement of strings (medium)

subject

thinking

• dfs deep traversal: Note that traversal begins with an empty string instead of being the first. The purpose of dfs is to have the first bit participate in the traversal as well. The essence of dfs is to go back, not to be stuck to a left subtree and a right subtree.

Problem

• Recursion:

class Solution:
    def permutation(self, s: str) -> List[str]:
        res = []
        vis = [0]*len(s)

        def dfs(track):
            if len(track) == len(s) and track not in res:
                res.append(track)
                return 
            for j in range(len(s)):
                if vis[j]:continue
                vis[j] = 1
                dfs(track+s[j])
                # As each field's depth traversal completes, mark the zero position to facilitate the next depth traversal
                vis[j] = 0
        dfs('')
        return res
        

• Recursive improvements: 1.Repeated elements are pruned without repeating the arrangement (the method above is to use track not in res, but not traverse when composing) 2.Instead of repeating operations on immutable strings, use lists, and finally join 3. It is slower to take lists as parameters, so consider a new idea: swap each bit in a for loop with traditional dfs bits as parameters.

class Solution:
    def permutation(self, s: str) -> List[str]:
        tmp, res = list(s), []
        def dfs(n):
            if n == len(tmp) - 1:
                res.append(''.join(tmp))
                return
            cutset = set()
            for i in range(n, len(tmp)):
                if tmp[i] in cutset: continue 
                cutset.add(tmp[i])
                tmp[i], tmp[n] = tmp[n], tmp[i]  # Swap, fix tmp[i] i n position n
                dfs(n + 1)                       # Open Fixed n + 1 Character
                tmp[i], tmp[n] = tmp[n], tmp[i]  # Resume exchange
        dfs(0)
        return res

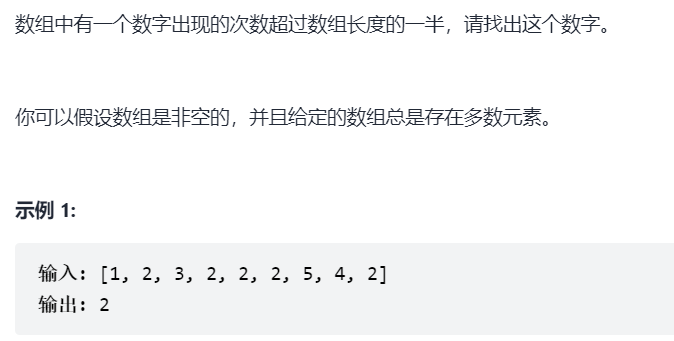
Sword Finger Offer 39.Numbers in arrays that occur more than half the time

subject

thinking

This is a very classic topic, and there are many ideas that will be written here, while the solutions given below only give some of the less common ones (the latter three).

• Hash table: Loops through the array, adds each element to the hash map, and returns the key with the largest value in the hash map
• Sorting: Of course, you can use many sort algorithms. If you write a heap sort yourself, you only need O(1). (Each local variable in a heap sort has a stack area, which is automatically allocated and released by the compiler, so we don't care about spatial complexity.) Sorting, python libraries are really fast, whether sorting or other 2333
• Randomization: Probability greater than 1/2 can be solved by randomization!
• Divide and conquer: the majority is still at least a part of the majority after dividing
• Boyer-Moore voting algorithm (spatial complexity O(1))
  
  The principle of this method is difficult to prove and can be understood as: different cancels out. When candidates are the real majority, count is the real count, otherwise count and real count are the opposite of each other. Because the value of count changes candidates when it becomes 0, count must be non-negative, so in the last paragraph, count must be the real count.Candidates is also a true majority.

Problem

• Randomization:

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        majority_count = len(nums) // 2
        while True:
            candidate = random.choice(nums)
            if sum(1 for elem in nums if elem == candidate) > majority_count:
                return candidate
                

• Divide and treat:

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        def majority_element_rec(lo, hi) -> int:
            if lo == hi:
                return nums[lo]

            mid = (hi - lo) // 2 + lo
            left = majority_element_rec(lo, mid)
            right = majority_element_rec(mid + 1, hi)

            left_count = sum(1 for i in range(lo, hi + 1) if nums[i] == left)
            right_count = sum(1 for i in range(lo, hi + 1) if nums[i] == right)
			# Find out which side contains the majority
            return left if left_count > right_count else right

        return majority_element_rec(0, len(nums) - 1)

• Voting Method:

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        count = 0
        candidate = None

        for num in nums:
            if count == 0:
                candidate = num
            count += (1 if num == candidate else -1)

        return candidate
        

Swordfinger Offer 40.Minimum k

subject

thinking

The easiest thing to think of is sorting: here are two sorting methods. A systematic review of sorting algorithms is described in this article and has not been written yet This section only describes the application of the current question

• Quick Platoon: Quick Platoon is actually the continuous repetition of "Sentry Division" and "Recursion". The process of sentry division is the continuous exchange of two pointers, the process of approaching, and the process of recursion is the solution of sub-problems. Look at a Quick Platoon template:

	def partition(i, j):
	    while i < j:
	        while i < j and arr[j] >= arr[l]: j -= 1
	        while i < j and arr[i] <= arr[l]: i += 1
	        arr[i], arr[j] = arr[j], arr[i]
	    arr[l], arr[i] = arr[i], arr[l]
	    return i
	    
	def quick_sort(arr, l, r):
		i = partition(l, r)
	    # Recursive left (right) subarray for sentinel division
	    quick_sort(arr, l, i - 1)
	    quick_sort(arr, i + 1, r)

Then you will find that this question only needs to go back to the first k, which is big and does not require sorting, so as long as it is divided into k+1 digits, the first k digits are already divided

• Heap sorting: Maintain a large top heap of k size, note that the k size, each time compared with the top, if the current number is greater than the top, skip, otherwise heap, and then heap the top (the largest element), so that the minimum k is left. Time complexity is O(NlogK).

Problem

• Quick Row:

class Solution:
    def getLeastNumbers(self, arr: List[int], k: int) -> List[int]:
        if k >= len(arr): return arr
        def quick_sort(l, r):
            i, j = l, r
            while i < j:
                while i < j and arr[j] >= arr[l]: j -= 1
                while i < j and arr[i] <= arr[l]: i += 1
                arr[i], arr[j] = arr[j], arr[i]
            arr[l], arr[i] = arr[i], arr[l]
            # Quick drain is the process of exchanging arrays constantly, only the first k are needed to drain
            if k < i: return quick_sort(l, i - 1) 
            if k > i: return quick_sort(i + 1, r)
            return arr[:k]
            
        return quick_sort(0, len(arr) - 1)
        

• Heap sorting:

from heapq import *

class Solution:
    def getLeastNumbers(self, arr: List[int], k: int) -> List[int]:
        if k==0: return []
        Bheap = []
        for num in arr:
            if len(Bheap)<k:
                heappush(Bheap, -num)
            # Unable to compare with pop, resulting in a bomb heap
            elif -num > Bheap[0]:
                heappushpop(Bheap, -num)
            else: continue
        return [-num for num in Bheap]
        

Swordfinger Offer 41.Median in data flow (difficult)

subject

thinking

• It's easy to do, but it's more difficult to do it with optimal space-time complexity. The problem with the median is sort + take, where the complexity is *O(NlogN)*m. Consider maintaining two heaps, one enlarged number and one reduced number so that the median can be obtained directly.
  • Then the insertion order should be one small, one large... For example, we stipulate that even numbers, take two heap tops/2 and add them to A; odd numbers, A is one more than B, take the top of A and add them to B.
  • But how can I keep the small one always on the small one and the big one on the big one? The answer is: If I want to insert the small one, I put it in the big one first, and then put the smallest one in the big one in the small one.
• In addition, in God K's puzzle it is mentioned: Push item on the heap, then pop and return the smallest item from the heap.The combined action runs more efficient than heappush () followed by a separate call to heappop ()., so intermediate logic can be combined and will be more efficient.

Problem

class Solution:
# heapq in python implements a small top heap, so a large top heap needs to be negative!
from heapq import *

class MedianFinder:
    def __init__(self):
        self.A = [] 	# Small-top heap, half larger
        self.B = [] 	# Top heap, keep smaller half

    def addNum(self, num: int) -> None:
        if len(self.A) != len(self.B):
            heappush(self.A, num)
            heappush(self.B, -heappop(self.A))
            # Writing of merge: heappush(self.B, -heappushpop(self.A, num))
        else:
            heappush(self.B, -num)
            heappush(self.A, -heappop(self.B))
            # Writing of merge: heappush(self.A, -heappushpop(self.B, -num)

    def findMedian(self) -> float:
        return self.A[0] if len(self.A) != len(self.B) else (self.A[0] - self.B[0]) / 2.0

Swordfinger Offer 42. Maximum sum of consecutive subarrays

subject

thinking

• Dynamic Planning: Use maxnum to record the maximum value that occurs at any time, and sum will add up until it is certain that the sum will not contribute positively, counting again

Problem

• Dynamic Planning:

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        sum = maxnum = nums[0]
        for _ in nums[1:]:
            # As long as the sum is positive, it is a positive contribution to the final result and can be retained
            # Otherwise sum is negative, we might as well start over
            sum = sum + _ if sum>0 else _
            maxnum  = max(sum, maxnum)
        return maxnum

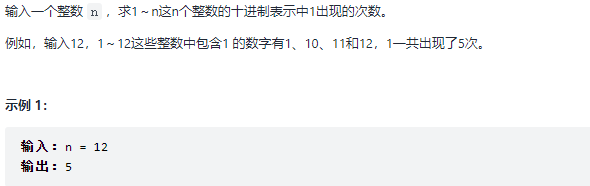
Number of occurrences of 1 in Offer 43.1-n integers of the sword finger (difficult)

subject

thinking

It's really too difficult, I won't. The following question refers to a python version translated from user@fine b in the commentary area. I'll give you a general idea:
First, determine the overall use of recursion, such as 1234 and 2345, which are also four digits, first count how many of the highest (in this case, thousands) contributions are, and finally, how many 1 of the 234 and 345 are contributed respectively.

• First of all, there is a rule: there are 20 in 99, 300 in 999 and 4000 in 9999. We count this number as base.
• There are two scenarios for top contributions:
  • Thousands are 1: 300 contributions in 999, plus a few contributions when more than 1000 are removed (234 from 1000 to 1234, but since 1000 is not added, the expression should be n-base+1)
  • Thousands are not 1: Thousands are high, and the cycles have contributed a high*base (2*99 out of 2345), plus 1000 from 1000 to 1999 starting with 1 (add these 1000 regardless of 2, 3, 4...), so the expression is high*base + 1000
• And then add the boundary condition, and the recursive relationship, up the code!

Problem

class Solution:
    def countDigitOne(self, n: int) -> int:
        if n == 0: return 0
        if n < 10: return 1
        # See how many digits this is
        digit = len(str(n))
        base = (digit-1)*pow(10, digit-2)
        # The current order of magnitude, which is also the highest non-1 number to be added
        exp = pow(10, digit-1)
        high = n//exp
        if high == 1:
            return base + n + 1-exp + self.countDigitOne(n-high*exp)
        else:
            return base*high + exp + self.countDigitOne(n-high*exp)

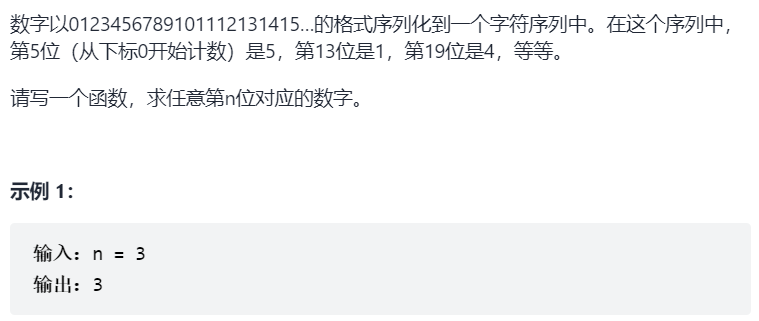
Offer 44. A digit in a number sequence (medium)

subject

thinking

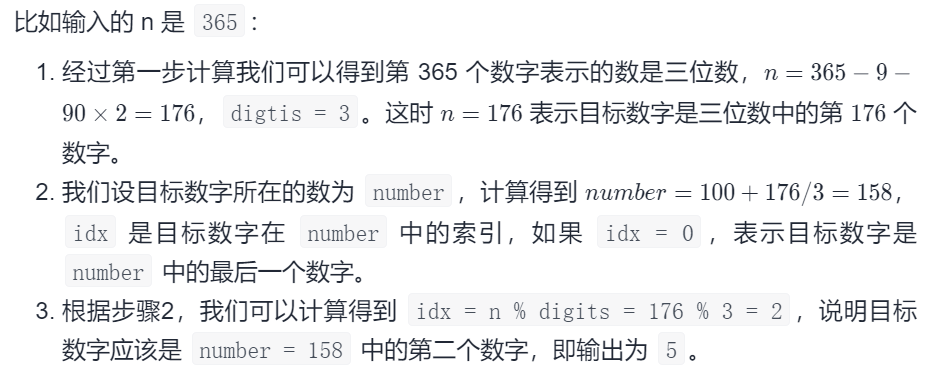
Find a regular question. Just remember and break it down into three steps:

• Find out how many digits this is
• Find out how far away from the smallest number of digits, and get the number by distance//number of digits
• Find out which number this position is in this number

For instance:

Problem

class Solution:
    def findNthDigit(self, n: int) -> int:
        # One digit occupies 9 places, two digits 10*2* (10-1) places, and three digits 10*3*10* (10-1) places
        # N digits occupy 9*10^(n-1)*n digits
        digit, exp, count = 1, 1, 9
        while n > count:
            n -= count
            exp *= 10
            digit += 1
            count = 9 * exp * digit
        start = exp
        # Because the subtraction ends with 9, you need n-1 here to start with 0 and the remaining distance
        num = start + (n-1) // digit
        return int(str(num)[(n-1) % digit])

Swordfinger Offer 45.Arrange the array into the smallest number (medium)

subject

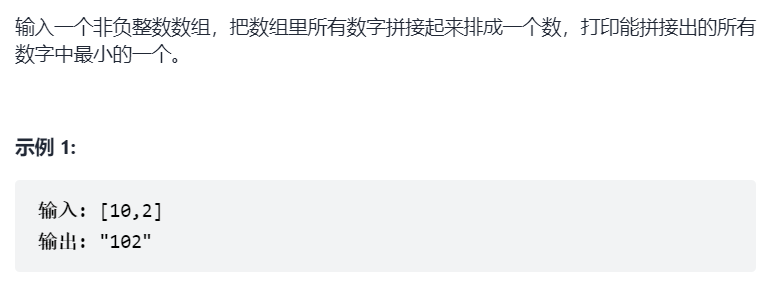
thinking

• Greedy algorithm: put a smaller number in front. But this smaller definition should be, bit by bit comparison, return to the bit by bit small, and look again, in fact, the rules have given us, that is
  
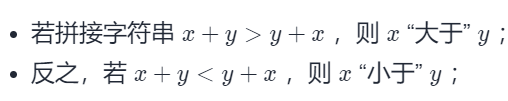
  The remaining problem is that you can customize the sorting, and you can apply any sort (quick row, bubble...) when the definition is complete.

Problem

• Several sorting algorithms will be summarized later: Algorithmic review, not written yet
• Tuning, defining rules, time complexity of built-in functions O(NlogN)

class Solution:
    def minNumber(self, nums: List[int]) -> str:
        def sort_rule(x, y):
            str1, str2 = x + y, y + x
            if str1 > str2: return 1
            elif str1 < str2: return -1
            else: return 0
        
        strs = [str(num) for num in nums]
        strs.sort(key = functools.cmp_to_key(sort_rule))
        return ''.join(strs)

Sword Finger Offer 46.Translate numbers to strings (medium)

subject

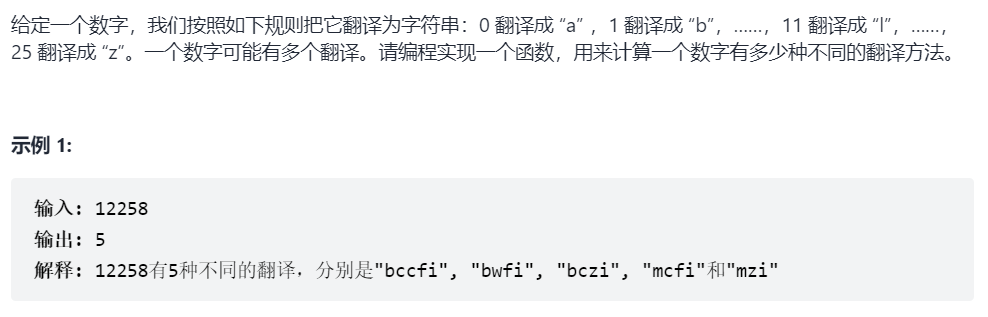
Analysis

• Recursion, where you choose to look backwards and forwards (the same is true from front to back, but it's not easy to get the rest):
  • Boundary condition: if the number is between 0 and 10, return 1
  • Recursive relationships: the first and second last digits can make up 10-25, then there are two combinations of the two, the combination or is single, corresponding to the remaining num//100 and num/10, in fact, especially like that one Frog Jumping Step Problem The common point of these two questions is that instead of choosing or not, they choose Aor to choose B. Combining the two choices A and B together is the total situation that can be selected at this step. If the first and second last digits do not make up 10~For numbers between 25, the recursion is num/10, for example 9999, with only one division.
• Dynamic Planning: Recursive "recursion" is dynamic planning when the recursive subproblem is clear! And dynamic planning uses only i-1 and i-2, which can be further simplified by replacing three (or even two) variables directly. The following figure is a good understanding that initializing dp[len(num)] to 1 may occur in two situations for the second to last character.
  

Problem

• Recursion:

class Solution:
    def translateNum(self, num) :
        if num < 10 : return 1
        
        if 10 <= num % 100 <= 25 :
            return self.translateNum(num // 10) + self.translateNum(num // 100)
        else :
            return self.translateNum(num // 10)

• Dynamic Planning:

class Solution:
    def translateNum(self, num: int) -> int:
        fstnum = secnum = 1
        # y is one, x is ten
        y = num % 10
        while num != 0:
            num //= 10
            x = num % 10
            fstnum, secnum = (fstnum + secnum if 10 <= 10 * x + y <= 25 else fstnum), fstnum
            y = x
        return fstnum

Swordfinger Offer 47.Maximum value of gifts (medium)

subject

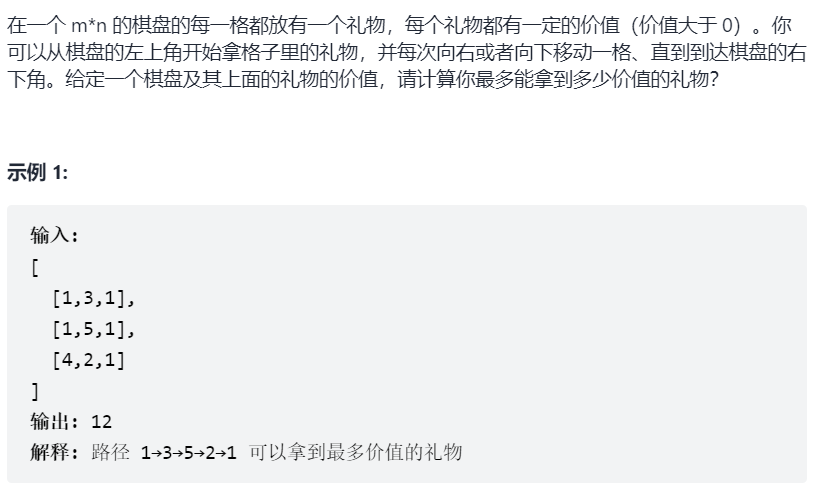
thinking

• Come on, plan dynamically, record current value, end point at the end anyway, because wherever you go, you can continue to add up down (right)
• Dynamic programming generally has two improvements:
  • When the grid matrix is large, only a very small number of cases occur where i=0 or j = 0, and a considerable loop redundant one judgement per round. Therefore, the first row and column of the matrix can be initialized before the recursion begins.
  • Or a common method is to open one more row and one column of space, initialize to zero, traverse from 1, subscript to dp[i-1][j-1], without judging the boundary, in this question you cannot open more space if you use in-place coverage, otherwise you will overwrite.
  • Override traversal! You can directly override in place if you don't need to return data that is in use of grid s (only dp[i-1][j], dp[i][j-1], dp[i][j]).

Problem

• Code I wrote:

class Solution:
    def maxValue(self, grid: List[List[int]]) -> int:
        dp = []
        INF = float("-inf")
        for row in range(0,len(grid)):
            dp.append([INF]*len(grid[0]))
        dp[0][0] = grid[0][0]
        for row in range(0,len(grid)):
            for col in range(0,len(grid[0])):
                dp[row][col] = max(dp[row][col-1]+grid[row][col] if col!=0 else INF, dp[row-1][col]+grid[row][col] if row!=0 else INF, grid[row][col])
        return dp[-1][-1]

• Overwrite in place + Initialize a row-by-column version (or God K):

class Solution:
    def maxValue(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        for j in range(1, n): # Initialize the first line
            grid[0][j] += grid[0][j - 1]
        for i in range(1, m): # Initialize the first column
            grid[i][0] += grid[i - 1][0]
        for i in range(1, m):
            for j in range(1, n):
                grid[i][j] += max(grid[i][j - 1], grid[i - 1][j])
        return grid[-1][-1]

Author: jyd
 Links: https://leetcode-cn.com/problems/li-wu-de-zui-da-jie-zhi-lcof/solution/mian-shi-ti-47-li-wu-de-zui-da-jie-zhi-dong-tai-gu/
Source: Force buckle ( LeetCode)
Copyright is owned by the author. For commercial reprinting, please contact the author for authorization. For non-commercial reprinting, please indicate the source.

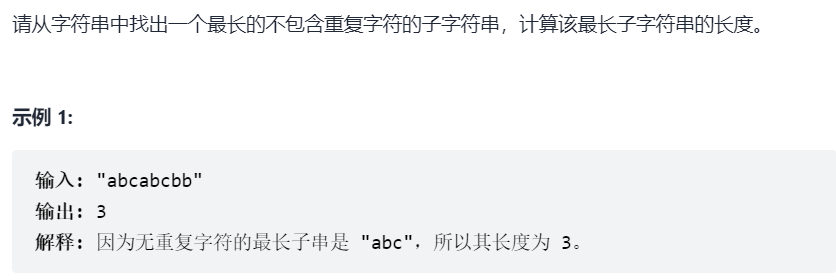
Swordfinger Offer 48. Longest substring without duplicate characters (medium)

subject

thinking

• Dynamic Programming + Linear Traversal: Traverse right until it stops, n o more questions are given, more general o(n^2).
• Dynamic Planning + Hash Table:
  • There is no need for a two-dimensional record. Simply remove the element before the repeating element from the dictionary, which is equivalent to a recount (where the recount does not start from 1 when the repeating element is encountered, but from the index before index-because the elements in between are different).
  • Another point is that by simply returning the maximum length instead of a specific substring, we can directly omit the dynamically programmed array and record it with a variable!
• Sliding window: essentially the same as the second method, but more intuitively limited by a left boundary

Problem

• Dynamic Planning + Hash:

class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        chardict = dict()
        cnt, maxcnt  = 0,0
        for index in range(0,len(s)):
            if s[index] in chardict and cnt >= index - chardict[s[index]]:
                cnt = index - chardict[s[index]]
                # For ease of understanding, if a duplicate character occurs, the record needs to be cancelled before the (first) duplicate character
                # In fact, it is a function of the above judgments of "current cumulative length" and "whether duplicate elements are in the interval"
                # for key,value in list(chardict.items()):
                    # if value<chardict[s[index]]:
                        # chardict.pop(key)
            else:
                cnt += 1
            chardict[s[index]] = index    
            maxcnt = max(cnt,maxcnt)
        return maxcnt

• Look at God K's dynamic plan and cancel the branch directly. If you can't get +1 anyway, I'll just go back to the default value of -1.

class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        dic = {}
        res = tmp = 0
        for j in range(len(s)):
            i = dic.get(s[j], -1) # Get Index i
            dic[s[j]] = j # Update Hash Table
            tmp = tmp + 1 if tmp < j - i else j - i # dp[j - 1] -> dp[j]
            res = max(res, tmp) # max(dp[j - 1], dp[j])
        return res

Author: jyd
 Links: https://leetcode-cn.com/problems/zui-chang-bu-han-zhong-fu-zi-fu-de-zi-zi-fu-chuan-lcof/solution/mian-shi-ti-48-zui-chang-bu-han-zhong-fu-zi-fu-d-9/
Source: Force buckle ( LeetCode)
Copyright is owned by the author. For commercial reprinting, please contact the author for authorization. For non-commercial reprinting, please indicate the source.

• Slide window:

class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        dic, res, left = {}, 0, -1
        for right in range(len(s)):
            if s[right] in dic:
            	# If the current left pointer is already after a repeating element, there is no need to update it
                left = max(dic[s[right]], left) 
            dic[s[right]] = right 
            res = max(res, right - left) 
        return res