[template] strict minor spanning tree \ color{green}{\text {[template] strict minor spanning tree}}} [template] strict minor spanning tree

[general idea of the topic]: [general idea of the topic]: little C has recently learned many algorithms of minimum spanning tree, Prim algorithm, Kurskal algorithm, loop elimination algorithm, etc. Just when little C is complacent, little p pours cold water on little c again. According to small P, let small C find a sub small spanning tree of an undirected graph, and the sub small spanning tree must be strictly sub small. That is to say, if the edge set selected by the minimum spanning tree is EME mem and the edge set selected by the strict sub small spanning tree is ese SES, then it needs to meet the following requirements: (value(e)value(e)value(e) represents the weight of edge eee)

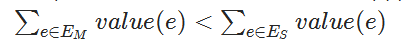
[idea]: \ color{blue} {[idea]:} [idea]: first find the minimum spanning tree of the original graph, and then we consider how to turn the minimum spanning tree into a strictly sub small spanning tree.

We find that the strict sub small spanning tree is different from the minimum spanning tree with only one edge. So we can enumerate which side that side is.

Suppose that the edge we add is an edge (u,v)(u,v)(u,v). After adding, there must be a ring, so we can delete the largest edge on the ring except (u,v)(u,v)(u,v). When the maximum edge weight is = = = (u,v)(u,v)(u,v) (U, V), the strict degree can be deleted.

The maximum edge weight and the strictly minor edge weight can be obtained by multiplication.

[Code]: \ color{blue} {[Code]:} [Code]:

typedef long long ll;
const int N=1e5+100;
const int M=3e5+100;
struct edge{
	int next,to;ll len;
}e[N<<1];int h[N],tot;
inline void add(int a,int b,ll w){
	e[++tot]=(edge){h[a],b,w};h[a]=tot;
	e[++tot]=(edge){h[b],a,w};h[b]=tot;
}
struct node{
	int u,v;ll w;bool chose;
	node(int _u=0,int _v=0,ll _w=0,bool _c=false){
		u=_u;v=_v;w=_v;chose=_c;
	}
	bool operator < (node c) const{
		return w<c.w;
	}
}a[M<<1];
struct union_set{
	int f[N],s[N];
	void init(int n){
		for(int i=1;i<=n;i++){
			f[i]=i;s[i]=1;
		}
	}
	int getf(int x){
		if (f[x]==x) return x;
		return f[x]=getf(f[x]);
	}
	void merge(int x,int y){
		int a=getf(x),b=getf(y);
		if (a==b) return;
		if (s[a]<s[b]) swap(a,b);
		f[b]=a;s[a]+=s[b];
	}
	bool query(int x,int y){
		return getf(x)==getf(y);
	}
}F;int n,m;ll cnt;
inline void kruskal(){
	sort(a+1,a+m+1);F.init(n);
	for(int i=1;i<=m;i++)
		if (!F.query(a[i].u,a[i].v)){
			F.merge(a[i].u,a[i].v);
			add(a[i].u,a[i].v,a[i].w);
			cnt+=a[i].w;a[i].chose=true;
		}
}
const ll inf=1ll<<62ll;
ll dep[N],f[N][22],maxn[N][22],minn[N][22];
void dfs_init(int u,int fa){
	dep[u]=dep[fa]+1;
	for(int i=0;i<20;i++){
		f[u][i+1]=f[f[u][i]][i];
		maxn[u][i+1]=max(maxn[u][i],maxn[f[u][i]][i]);
		minn[u][i+1]=max(minn[u][i],minn[f[u][i]][i]);
		if (maxn[u][i]>maxn[f[u][i]][i])
			minn[u][i+1]=max(minn[u][i+1],maxn[f[u][i]][i]);
		else if (maxn[u][i]<maxn[f[u][i]][i])
			minn[u][i+1]=max(minn[u][i+1],maxn[u][i]);
	}
	for(int i=h[u];i;i=e[i].next){
		register int to=e[i].to;
		if (to==fa) continue;
		f[to][0]=u;minn[to][0]=-inf;
		maxn[to][0]=e[i].len;
		dfs_init(to,u);
	}
}
int lca(int u,int v){
	if (dep[u]<dep[v]) swap(u,v);
	for(int i=20;i>=0;i--)
		if (dep[f[u][i]]>=dep[v])
			u=f[u][i];
	if (u==v) return u;
	for(int i=20;i>=0;i--)
		if (f[u][i]!=f[v][i])
			u=f[u][i],v=f[v][i];
	return f[v][0];
}
ll query(int u,int LCA,ll t){
	register ll ans=-inf;
	for(int i=20;i>=0;i--)
		if (dep[f[u][i]]>=dep[LCA]){
			if (t!=maxn[u][i]) ans=max(ans,maxn[u][i]);
			else ans=max(ans,minn[u][i]);
			u=f[u][i];
		}
	return ans;
}
ll ans,res;int ret;
int main(){
	n=read();m=read();ans=inf;
	for(int i=1;i<=m;i++){
		a[i].u=read();
		a[i].v=read();
		a[i].w=read();
	}
	kruskal();dfs_init(1,0);
	for(int i=1;i<=m;i++)
		if (!a[i].chose){
			ret=lca(a[i].u,a[i].v);
			res=query(a[i].u,ret,a[i].w);
			res=max(res,query(a[i].v,ret,a[i].w));
			ans=min(ans,cnt-res+a[i].w);
		}
	printf("%lld",ans);
	return 0;
}