HDU 6686 Rikka with Travels
What is the probability of choosing two disjoint paths on a tree? The path length is defined as the number of vertices of the path.
Solutions:
Preliminary thinking and observing examples show that the two paths are orderly pairs, [2,1], [1,2] are not the same. Let's assume that you already know the length of a path you choose is l. Just find out what the longest path is for removing the path from the tree. Suppose rrr is the longest path for the remaining forest. Suppose rrr is the number of paths with the length of lll. Then find out the corresponding rrr is the contribution. Then sum all the contributions of LLL is the answer.
Obviously, it's time-out, and there's no way to start. So we continue to optimize. For a tree, we split one side at a time.
[External Link Picture Transfer Failure (img-orlPQath-1566221022148)(https://i.loli.net/2019/08/19/C4iJcIWeYmh1GSl.png)]
The diameter of the left subtree is L, and the diameter of the right subtree is R. We can find that the path of the left subtree may be 1,2,...&ThinSpace,...&ThinSpace,... L1,2,... L1,2,... cdots, L1,2,...&ThinSpace,... L1,2,... , R1,2,......... cdots, R1,R1,2,.................. Cdots, R1,2,............... R, we can know that the interval= [1,L] l=[1,L]l=[1,L]l=[1,L] l= [1, L] 1, L] [1] [1, L] L] contribution to the contribution of RRR l=[1,R]l=[1,R] Update to LLL, write violent modification is
f[i]=max(f[i],R),1&lt;=i&lt;=lf[i]=max(f[i],L),1&lt;=i&lt;=R f[i]=max(f[i],R),1&lt;=i&lt;=l \\ f[i]=max(f[i],L),1&lt;=i&lt;=R f[i]=max(f[i],R),1<=i<=lf[i]=max(f[i],L),1<=i<=R
The modification violence is definitely timed out, but Teacher Ji's segment tree can be updated within O(log2(n))O(log^2(n))O(log2(n)). After careful consideration, we can find that f [i-1]>= f [i], so we can directly f[l]=max(f[l],R),f[r]=max(L,f[l]), and then do f[i]=max(f[i],f[i+1], which can achieve the same result, complexity O(1).
For how to calculate the contribution, the following problem is how to calculate the diameter of the subtree. Needless to say, it must be a tree DP. The tree DP holds two values. One is the longest path of the leaf under the node, and the other is the longest path of the subtree. There are two situations in the longest path, one is through oneself, the other is from one of one's sons. Twice DFS can solve this problem.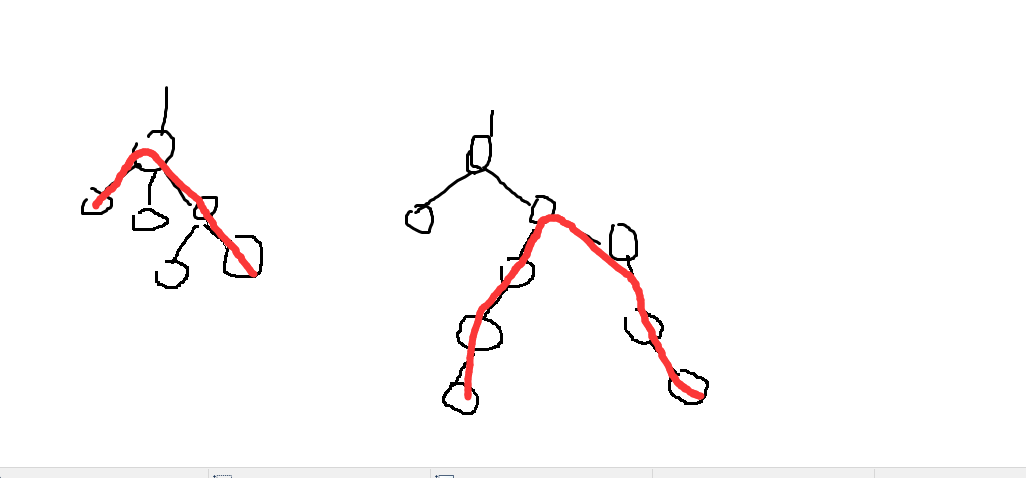

#include "bits/stdc++.h"

using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> P;
#define VNAME(value) (#value)
#define bug printf("*********\n");
#define debug(x) cout<<"["<<VNAME(x)<<" = "<<x<<"]"<<endl;
#define mid ((l + r) >> 1)
#define chl 2 * k + 1
#define chr 2 * k + 2
#define lson l, mid, chl
#define rson mid + 1, r, chr
#define eb(x) emplace_back(x)
#define pb(x) emplace_back(x)
#define mem(a, b) memset(a, b, sizeof(a));

const LL mod = (LL) 1e9 + 7;
const int maxn = (int) 1e6 + 5;
const LL INF = 0x7fffffff;
const LL inf = 0x3f3f3f3f;
const double eps = 1e-8;

#ifndef ONLINE_JUDGE
clock_t prostart = clock();
#endif

void f() {
#ifndef ONLINE_JUDGE
    freopen("../data.in", "r", stdin);
#endif
}

//typedef __int128 LLL;

template<typename T>
void read(T &w) {//Read in
    char c;
    while (!isdigit(c = getchar()));
    w = c & 15;
    while (isdigit(c = getchar()))
        w = w * 10 + (c & 15);
}

template<typename T>
void output(T x) {
    if (x < 0)
        putchar('-'), x = -x;
    int ss[55], sp = 0;
    do
        ss[++sp] = x % 10;
    while (x /= 10);
    while (sp)
        putchar(48 + ss[sp--]);
}

int T, n;

vector<int> G[maxn];
int dp[maxn], mx[maxn];

void dfs(int r, int p, int dep) {
    for (auto au:G[r]) {
        if (au != p) {
            dfs(au, r, dep + 1);
            dp[r] = max(dp[au], max(dp[r], mx[au] + 1 + mx[r]));
            mx[r] = max(mx[au] + 1, mx[r]);
        }
    }
}

int ans[maxn];

void dfs2(int r, int p, int dep) {
    if (p != -1) {
        ans[dp[r] + 1] = max(ans[dp[r] + 1], dp[p] + 1);
        ans[dp[p] + 1] = max(ans[dp[p] + 1], dp[r] + 1);
    }
    int mx1 = -1, mx2 = -1, d = -1;
    dp[r] = 0;
    mx[r] = 0;
    for (auto au:G[r]) {  //Judge the longest diameter, the biggest path and the second short path
        if (mx1 == -1 || d == -1) {
            mx1 = au;
            d = au;
        } else {
            if (dp[au] > dp[mx1]) {
                d = au;
            }
            if (mx[au] >= mx[mx1]) {
                mx2 = mx1;
                mx1 = au;
            } else if (mx2 == -1 || mx[au] > mx[mx2]) {
                mx2 = au;
            }
        }
        dp[r] = max(dp[au], max(dp[r], mx[au] + 1 + mx[r]));
        mx[r] = max(mx[au] + 1, mx[r]);
    }
    for (auto au:G[r]) {   //Update son from root node
        if (au == p)continue;
        if (au == mx1 || au == mx2 || au == d) {
            int tdp = dp[r], tmx = mx[r];
            dp[r] = 0;
            mx[r] = 0;
            for (auto a2:G[r]) {
                if (a2 != au) {
                    dp[r] = max(dp[a2], max(dp[r], mx[a2] + 1 + mx[r]));
                    mx[r] = max(mx[a2] + 1, mx[r]);
                }
            }
            dfs2(au, r, dep + 1);
            dp[r] = tdp;
            mx[r] = tmx;
        } else {
            dfs2(au, r, dep + 1);
        }
    }
    dp[r] = 0;
    mx[r] = 0;
    for (auto au:G[r]) {//Backtracking and Renewal
        if (au != p) {
            dp[r] = max(dp[au], max(dp[r], mx[au] + 1 + mx[r]));
            mx[r] = max(mx[au] + 1, mx[r]);
        }
    }
}

int main() {
    f();
    read(T);
    while (T--) {
        read(n);
        for (int i = 0; i < n - 1; i++) {
            int u, v;
            read(u);
            read(v);
            G[u].emplace_back(v);
            G[v].emplace_back(u);
        }
        dfs(1, -1, 0);
        dfs2(1, -1, 0);
        LL res = 0;
        for (int i = n - 1; i >= 1; i--) {
            ans[i] = max(ans[i], ans[i + 1]);
            res = res + ans[i];
//            printf("%d%c", ans[i], i == 1 ? '\n' : ' ');
        }
        printf("%lld\n", res);
        for (int j = 0; j <= n; ++j) {
            G[j].clear();
            ans[j] = 0;
            dp[j] = 0;
            mx[j] = 0;
        }
    }
#ifndef ONLINE_JUDGE
    cout << "Running time:" << 1.0 * (clock() - prostart) / CLOCKS_PER_SEC << endl;
#endif
    return 0;
}