[title]

Title Description:

On L's bookshelf, there are N wonderful books, each of which is of great value.

M is A book lover. He has long coveted L's books. Finally, he can't bear the temptation. He thinks that in order to finish the task quickly, he doesn't want l to find out that there are fewer books. When he decides to steal books, he can choose at most B books and at least A books for any consecutive K books. Now he wants to know how to choose A book so that the sum of the value of the stolen book and the sum of the value of the remaining books is the biggest difference.

Input format:

First line four integers n, K, a, B

A line of N integers represents the value of each book

Output format:

An integer represents the answer

Sample data:

input

2 1 0 1
2 -2

output

4

remarks:

[sample explanation]

The sum of the value of getting the first book is 2

The sum of surplus value is - 2

The difference is 4

[data range]

For 20%: N ≤ 10

For the other 20%: a = 0, B = k

For 100%: N ≤ 1000, 0 ≤ A ≤ B ≤ K ≤ 10, the absolute value of all books ≤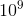

 

[analysis]

It's easy to think of the pressure in such a small range of K ≤ 10

Use f [i] [S] to indicate the answer whose former I personal status is s

Transfer from the previous (i - 1) bit

 

[Code]

Big guy's code

#include<bits/stdc++.h>
#define ll long long
#define N 1009
#define in read()
using namespace std;
ll val[N],f[N][1025];
int n,k,a,b; 
bool leg[1025];
inline int read(){
	char ch;int res=0;
	while((ch=getchar())<'0'||ch>'9');
	while(ch>='0'&&ch<='9'){
		res=(res<<3)+(res<<1)+ch-'0';
		ch=getchar();
	}
	return res;
}
void init(){
	int status=(1<<10);
	for(int i=0;i<status;++i){
		int num=0,h=i;
		while(h){
			if(h&1) num++;
			h>>=1;
		}
		if(num>=a&&num<=b)  leg[i]=1;
	}
}
int main(){
	n=in;k=in;a=in;b=in;
	init();	int maxn=(1<<k);
	ll sum=0;
	for(int i=1;i<=n;++i) {scanf("%lld",&val[i]);sum+=val[i];}
	memset(f,-1,sizeof(f));
	for(int i=0;i<maxn;++i) f[0][i]=0;
	for(int i=1;i<=n;++i){
		for(int s=0;s<maxn;++s){
			if(leg[s]){
				if(f[i-1][(s>>1)]!=-1){
					if(s&1)	f[i][s]=max(f[i][s],f[i-1][s>>1]+val[i]);
					else f[i][s]=max(f[i][s],f[i-1][s>>1]);
				}
				if(f[i-1][(s>>1)|(1<<k-1)]!=-1){
					if(s&1)	f[i][s]=max(f[i][s],f[i-1][(s>>1)|(1<<k-1)]+val[i]);
					else f[i][s]=max(f[i][s],f[i-1][(s>>1)|(1<<k-1)]);
				}
			}
		}
	}
	ll ans=0;
	for(int i=0;i<maxn;++i){
		if(f[n][i]==-1) continue;
		ans=max(ans,f[n][i]);
	}
	printf("%lld",2*ans-sum);
	return 0;
}