Topic link: http://acm.hdu.edu.cn/showproblem.php?pid=6143

The Title meaning gives m letters, and then compiles the ranking words. The name consists of the name and the name. The length of the name and the name is n.

Give m different characters, find out how many names can be arranged, names and names can not have the same characters, and names can not.

There are repetitions. The final answer is module 1e9+7.

When we select i from m characters to form a surname, the remaining m-i characters can be used to form a name.

The number of options for selecting characters from M characters to re-select I characters is as follows: C(m,i)

For the selected i-character, we can place the I-character at each position. There are a total of i^n methods, but

There's a lot of repetition. We need to subtract the repetition. What we want is a surname that happens to consist of i characters.

So we use i^n to subtract the exact i-1 character to form a surname, subtract the exact i-2 character to form a surname... until the exact one.

The final result of the scheme is that exactly i characters make up the surname, and then the scheme of selecting the i characters is formed.

For names, n positions, each character has M-I selection, and the corresponding combination of names is (m-i)^n.

Species.

The summary formula is as follows:

It shows that C[i,j] is the combination number of J selected from the number of I.

a[j] is the number of schemes in which exactly J characters make up the surname.

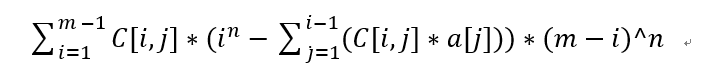
AC Code:

#include <iostream>
#include <stdio.h>
#include <string.h>

using namespace std;

typedef long long LL;
const int maxn = 2002;
const int mod = 1e9+7;
LL C[maxn][maxn];
LL a[maxn];   /// a[i] represents the number of schemes in which exactly one character is used to form a surname.
/// Tabulating Combination Number
void getCombination()
{
    memset(C,0,sizeof(C));
    C[1][0] = 1;
    C[1][1] = 1;
    for(int i = 2; i < maxn; i++)
    {
        C[i][0] = 1;
        for(int j = 1; j <= i+1; j++)
            C[i][j] = (C[i-1][j-1]+C[i-1][j])%mod;
    }
}
/// Fast power modulus of integers
LL Integer_QuickPow(LL n,LL k)
{
    LL ans,res;
    ans = 1;
    res = n;
    while(k)
    {
        if(k&1)
            ans = (ans*res)%mod;
        res = (res*res)%mod;
        k = k>>1;
    }
    return ans;
}
//Remove weight
LL Calculate_Sum(LL k,LL n)
{
    LL powerk = Integer_QuickPow(k,n);  /// Finding the n-th power of k
    LL sum = 0;
    for(int j = 1; j < k; j++)
    {
        sum = (sum+(C[k][j]*a[j])%mod)%mod;
    }
    LL ans = ((powerk-sum)%mod+mod)%mod;
    return ans;
}
//Solution
LL solve(LL n,LL m)
{
    LL ans = 0;
    a[0] = 0;
    for(int i = 1; i < m; i++)
    {
        a[i] = Calculate_Sum(i,n);
        LL power = Integer_QuickPow(m-i,n);
        ans = (ans+((C[m][i]*a[i]%mod)*power)%mod)%mod;
    }
    return ans;
}
int main()
{
    LL n,m;
    getCombination();
    int t;
    cin>>t;
    while(t--)
    {
        cin>>n>>m;
        cout<<solve(n,m)<<endl;
    }
    return 0;
}