13_JavaScript data structure and algorithm binary search tree

Keywords: Javascript Algorithm data structure Binary tree

JavaScript data structure and algorithm (XIII) binary search tree

Binary search tree

Binary Search Tree (BST), also known as binary sort tree and Binary Search Tree.

Binary search tree is a binary tree and can be empty.

If it is not empty, the following properties are met:

Condition 1: all key values of non empty left subtree are less than those of its root node. For example, the key values of all non empty left subtrees of node 6 in the third node are less than 6;
Condition 2: all key values of non empty right subtree are greater than those of its root node; For example, the key values of all non empty right subtrees of node 6 in the third node are greater than 6;
Condition 3: the left and right subtrees themselves are binary search trees;

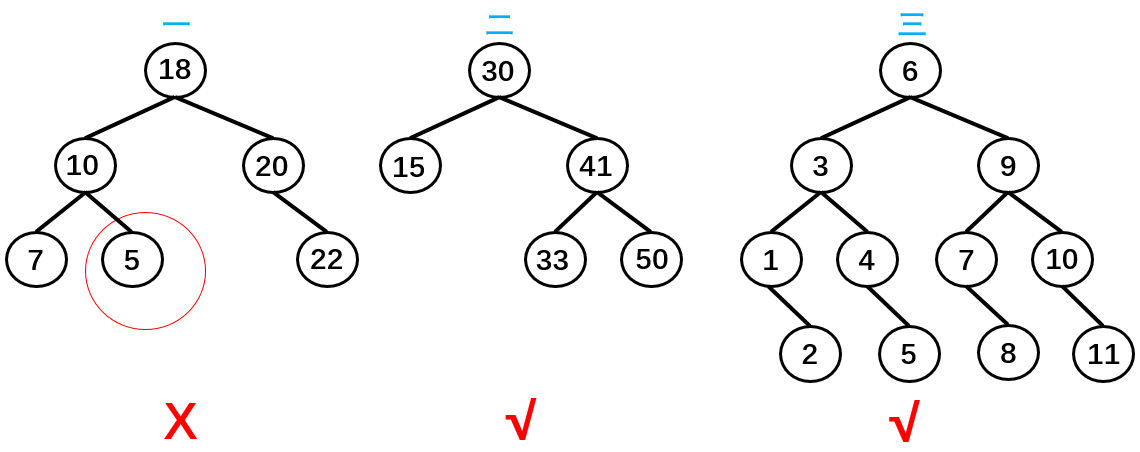
As shown in the above figure, tree 2 and tree 3 meet three conditions and belong to a binary tree. Tree 1 does not meet condition 3, so it is not a binary tree.

Summary: the main feature of binary search tree is that smaller values are always saved on the left node and relatively larger values are always saved on the right node. This feature makes the query efficiency of binary search tree very high, which is the source of "search" in binary search tree.

Application example of binary search tree

The following is a binary search tree:

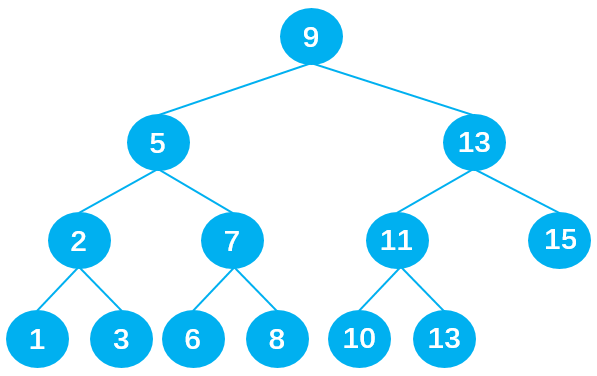
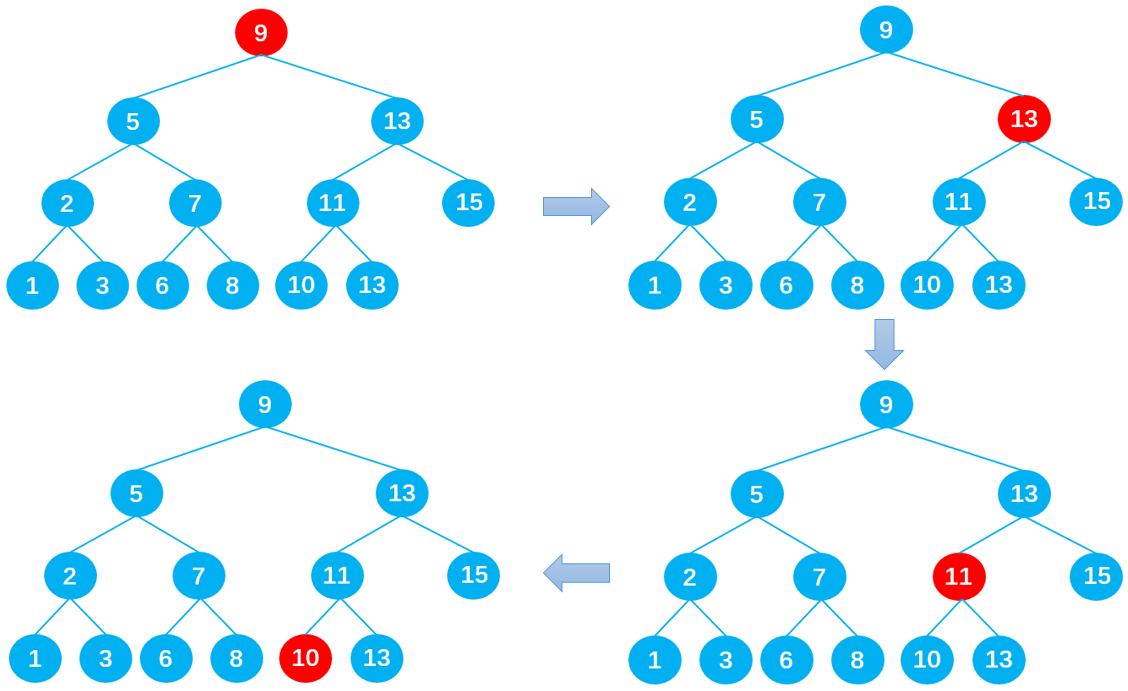
If you want to find data 10, you only need to find it four times, which is very efficient.

The first time: compare 10 with root node 9. Since 10 > 9, 10 is next compared with the right child node 13 of root node 9;
The second time: since 10 < 13, 10 is compared with the left child node 11 of the parent node 13 in the next step;
The third time: since 10 < 11, the next step is to compare 10 with the left child node 10 of the parent node 11;
The fourth time: since 10 = 10, the data 10 is finally found.

It is also 15 data. To query 10 data in the sorted array, you need to query 10 times:

In fact: if it is a sorted array, you can find it in two: 9 for the first time, 13 for the second time, 15 for the third time. We find that if the data of each binary is represented in the form of a tree, it is a binary search tree. This is why array dichotomy is efficient.

Encapsulation of binary search tree

The binary search tree has four basic attributes: the root pointing to the node, the key in the node, the left pointer and the right pointer.

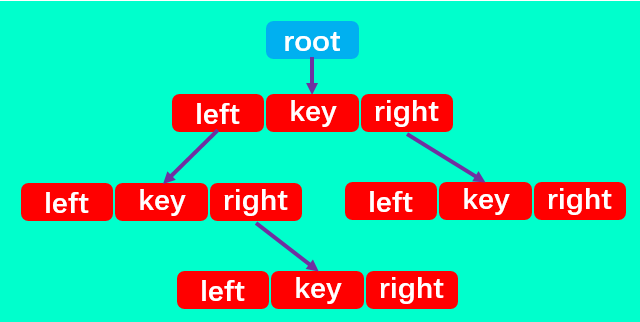
Therefore, in addition to defining the root attribute, a node internal class should also be defined in the binary search tree, which contains the left, right and key attributes of each node.

// Node class
class Node {
  constructor(key) {
    this.key = key;
    this.left = null;
    this.right = null;
  }
}

Common operations of binary search tree:

insert(key) inserts a new key into the tree.
search(key) finds a key in the tree. If the node exists, it returns true; If it does not exist, false is returned.
preOrderTraverse traverses all nodes in a preorder traversal manner.
inOrderTraverse traverses all nodes in a medium order traversal manner.
postOrderTraverse traverses all nodes by post order traversal.
min returns the smallest value / key in the tree.
max returns the largest value / key in the tree.
remove(key) removes a key from the tree.

insert data

Implementation idea:

First, create a node object based on the passed in key.
Then judge whether the root node exists. If it does not exist, use this.root = newNode to directly take the new node as the root node of the binary search tree.
If there is a root node, redefine an internal method insertNode() to find the insertion point.

insert(key) code implementation

// insert(key) inserts data
insert(key) {
  const newNode = new Node(key);

  if (this.root === null) {
    this.root = newNode;
  } else {
    this.insertNode(this.root, newNode);
  }

}

Implementation idea of insertNode():

According to the comparison of the two incoming nodes, always find the location where the new node is suitable for insertion until the new node is successfully inserted.

When newnode.key < node.key, look to the left:
- Case 1: when the node has no left child node, insert it directly:
- Case 2: when a node has a left child node, it recursively calls insertNode(). Until it encounters that no left child node is successfully inserted into a newNode, it no longer meets the situation, so it no longer calls insertNode(), and recursion stops.
When newnode. Key > = node.key, look to the right, which is similar to looking to the left:
- Case 1: when the node has no right child node, insert it directly:
- Case 2: when a node has a right child node, insertNode() is still called recursively until the node passed in the insertNode method has no right child node and successfully inserts a new node.

insertNode(root, node) code implementation

insertNode(root, node) {

  if (node.key < root.key) { // Look to the left and insert

    if (root.left === null) {
      root.left = node;
    } else {
      this.insertNode(root.left, node);
    }

  } else { // Look to the right and insert

    if (root.right === null) {
      root.right = node;
    } else {
      this.insertNode(root.right, node);
    }

  }

}

Traversal data

The traversal of the tree mentioned here is not only for binary search trees, but also for all binary trees. Since the tree structure is not a linear structure, there are many options for traversal. The three common binary tree traversal methods are:

Preorder traversal;
Middle order traversal;
Post order traversal;

There is also sequence traversal, which is less used.

Preorder traversal

The process of preorder traversal is as follows:

First, traverse the root node;
Then, traverse its left subtree;
Finally, traverse its right subtree;

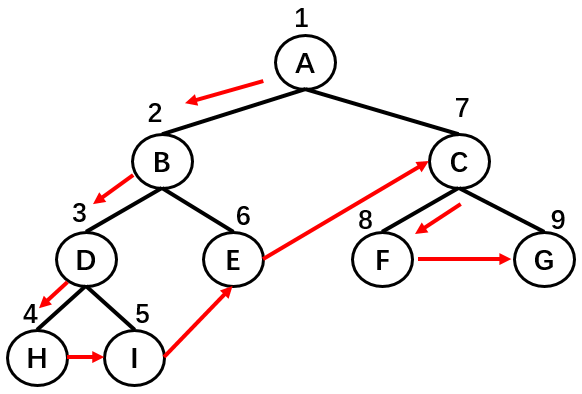
As shown in the above figure, the node traversal order of binary tree is: a - > b - > D - > H - > I - > e - > C - > F - > G.

Code implementation:

// Preorder traversal (left and right DLR)
preorderTraversal() {
  const result = [];
  this.preorderTraversalNode(this.root, result);
  return result;
}

preorderTraversalNode(node, result) {
  if (node === null) return result;
  result.push(node.key);
  this.preorderTraversalNode(node.left, result);
  this.preorderTraversalNode(node.right, result);
}

Medium order traversal

Implementation idea: the principle is the same as that of preorder traversal, but the traversal order is different.

First, traverse its left subtree;
Then, traverse the root (parent) node;
Finally, traverse its right subtree;

Process diagram:

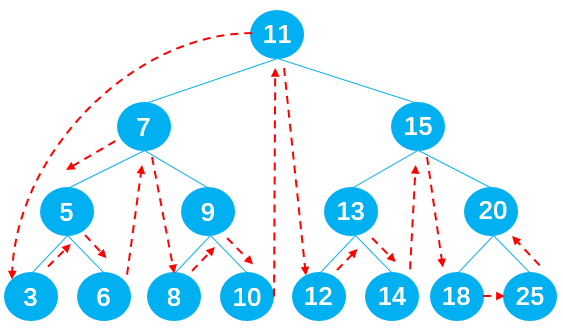
The order of output nodes shall be: 3 - > 5 - > 6 - > 7 - > 8 - > 9 - > 10 - > 11 - > 12 - > 13 - > 14 - > 15 - > 18 - > 20 - > 25.

Code implementation:

// Middle order traversal (left root right LDR)
inorderTraversal() {
  const result = [];
  this.inorderTraversalNode(this.root, result);
  return result;
}

inorderTraversalNode(node, result) {
  if (node === null) return result;
  this.inorderTraversalNode(node.left, result);
  result.push(node.key);
  this.inorderTraversalNode(node.right, result);
}

Postorder traversal

Implementation idea: the principle is the same as that of preorder traversal, but the traversal order is different.

First, traverse its left subtree;
Then, traverse its right subtree;
Finally, traverse the root (parent) node;

Process diagram:

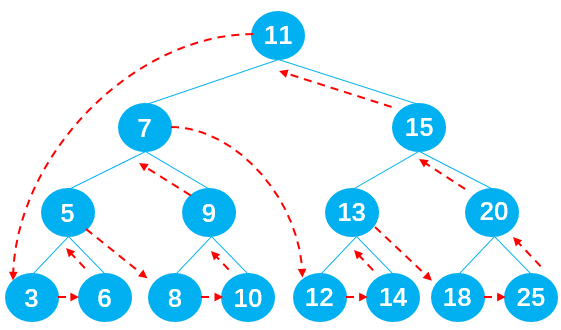
The order of output nodes should be: 3 - > 6 - > 5 - > 8 - > 10 - > 9 - > 7 - > 12 - > 14 - > 13 - > 18 - > 25 - > 20 - > 15 - > 11.

Code implementation:

// Post order traversal (left and right lrds)
postorderTraversal() {
  const result = [];
  this.postorderTraversalNode(this.root, result);
  return result;
}

postorderTraversalNode(node, result) {
  if (node === null) return result;
  this.postorderTraversalNode(node.left, result);
  this.postorderTraversalNode(node.right, result);
  result.push(node.key);
}

summary

Three traversal modes are distinguished by traversing the root (parent) node. For example: first order traversal first traverses the root node, second order traversal second traverses the root node, subsequent traversal last traverses the root node.

Find data

Find maximum or minimum

It is very simple to find the most value in the binary search tree. The minimum value is on the far left of the binary search tree and the maximum value is on the far right of the binary search tree. The maximum value can be obtained by searching all the way left / right, as shown in the following figure:

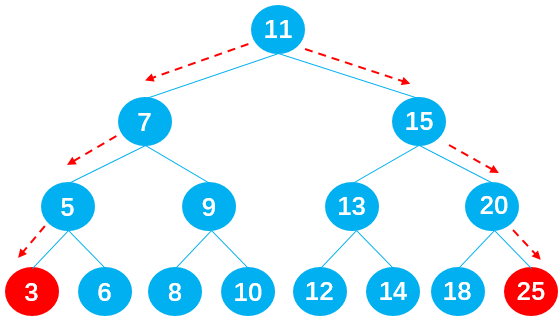
Code implementation:

// min() get the minimum value of binary search tree
min() {
  if (!this.root) return null;
  let node = this.root;
  while (node.left !== null) {
    node = node.left;
  }
  return node.key;
}

// max() gets the maximum value of the binary search tree
max() {
  if (!this.root) return null;
  let node = this.root;
  while (node.right !== null) {
    node = node.right;
  }
  return node.key;
}

Find a specific value

It is also very efficient to find specific values in the binary search tree. Just start from the root node and compare the key value of the node to be searched. If node.key < root, search to the left. If node.key > root, search to the right until null is found or found. You can use recursive implementation or loop implementation.

Code implementation:

// search(key) finds whether there are the same keys in the binary search tree. If there are, it returns true; otherwise, it returns false
search(key) {
  return this.searchNode(this.root, key);
}

// Recursive implementation
searchNode(node, key) {
  if (node === null) return false;
  if (key < node.key) {
    return this.searchNode(node.left, key);
  } else if (key > node.key) {
    return this.searchNode(node.right, key);
  } else {
    return true;
  }
}

// Through the while loop
search2(key) {

  let node = this.root;

  while (node !== null) {
    if (key < node.key) {
      node = node.left;
    } else if (key > node.key) {
      node = node.right;
    } else {
      return true;
    }
  }

  return false;

}

Delete data

Implementation idea:

Step 1: find the node to delete first. If it is not found, it does not need to be deleted;

First, define the variable current to save the node to be deleted, the variable parent to save its parent node, and the variable isLeftChild to save whether current is the left node of the parent, so as to change the direction of relevant nodes when deleting nodes later.

let currentNode = this.root;
let parentNode = null;
let isLeftChild = true;

// Cycle to find the node currentNode to be deleted, its parentNode and isLeftChild
while (currentNode.key !== key) {
  parentNode = currentNode;

  // Less than, look left
  if (key < currentNode.key) {
    isLeftChild = true;
    currentNode = currentNode.left;
  } else {
    // Otherwise, look to the right
    isLeftChild = false;
    currentNode = currentNode.right;
  }

  // If no equal nodes are found, false is returned
  if (currentNode === null) {
    return false;
  }
}

Step 2: delete the found specified node. There are three situations:

The leaf node is deleted;
Delete a node with only one child node;
Delete a node with two child nodes;

The leaf node is deleted

Leaf nodes are deleted in two cases:

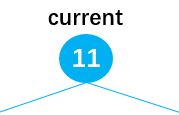
The leaf node is also the root node

When the leaf node is the root node, as shown in the following figure, at this time, current == this.root, directly delete the root node through: this.root = null.

The leaf node is not a root node

When the leaf node is not the root node, there are also two cases, as shown in the following figure

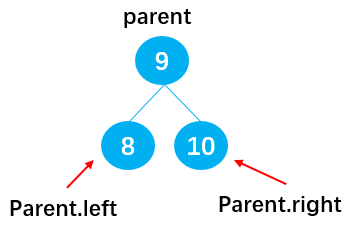
If current = 8, you can delete node 8 by: parent.left = null;

If current = 10, you can delete node 10 by: parent.right = null;

Code implementation:

// 1. Leaf nodes are deleted
if (currentNode.left === null && currentNode.right === null) {
  if (currentNode === this.root) {
    this.root = null;
  } else if (isLeftChild) {
    parentNode.left = null;
  } else {
    parentNode.right = null;
  }

  // 2. A node with only one child node is deleted
}

A node with only one child node is deleted

There are six situations:

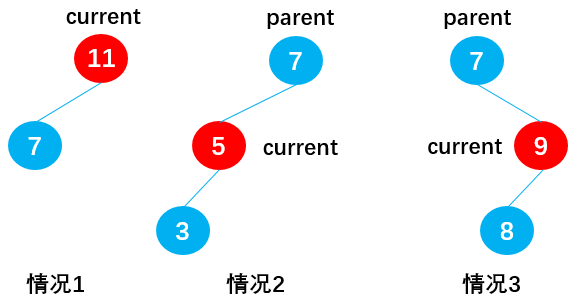
When there is a left child node in current (current.right == null):

Case 1: current is the root node (current == this.root), such as node 11. In this case, delete root node 11 by: this.root = current.left;
Case 2: current is the left child node of the parent node (isLeftChild == true). For example, node 5 is deleted by: parent.left = current.left;
Case 3: current is the right child node of the parent node (isLeftChild == false), such as node 9. In this case, delete node 9 through: parent.right = current.left;

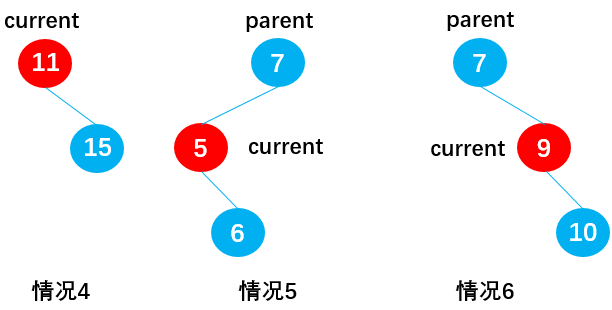
When there is a right child node in current (current.left = null):

Case 4: current is the root node (current == this.root), such as node 11. In this case, delete root node 11 through this.root = current.right.
Case 5: current is the left child node of the parent node (isLeftChild == true). For example, node 5 is deleted through: parent.left = current.right;
Case 6: current is the right child node of the parent node (isLeftChild == false), such as node 9. In this case, delete node 9 through: parent.right = current.right;

Code implementation:

// 2. A node with only one child node is deleted
} else if (currentNode.right === null) { // currentNode only has left node
  //--2.1. The currentNode only exists in the case of < left node >
  //----2.1.1. currentNode equals root
  //----2.1.2. parentNode.left equals currentNode
  //----2.1.3. parentNode.right equals currentNode

  if (currentNode === this.root) {
    this.root = currentNode.left;
  } else if (isLeftChild) {
    parentNode.left = currentNode.left;
  } else {
    parentNode.right = currentNode.left;
  }

} else if (currentNode.left === null) { // currentNode has only the right node
  //--2.2. The currentNode only exists in the case of < right node >
  //----2.1.1 currentNode equals root
  //----2.1.1 parentNode.left equals currentNode
  //----2.1.1 parentNode.right equals currentNode

  if (currentNode === this.root) {
    this.root = currentNode.right;
  } else if (isLeftChild) {
    parentNode.left = currentNode.right;
  } else {
    parentNode.right = currentNode.right;
  }

A node with two child nodes is deleted

This situation is very complex. Firstly, this problem is discussed according to the following binary search tree:

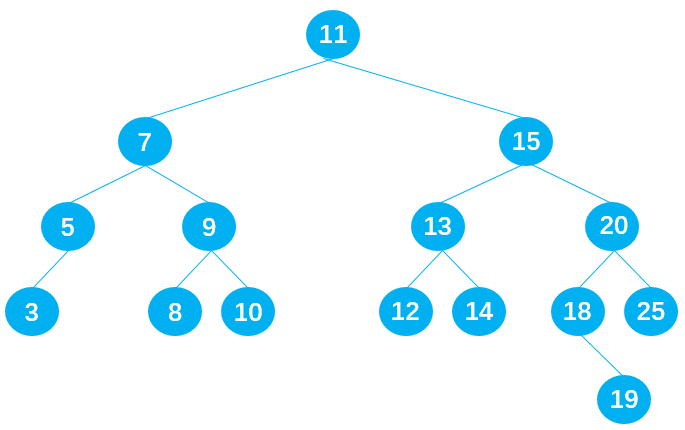
Delete node 9

There are two ways to ensure that the original binary tree is still a binary search tree after node 9 is deleted:

Method 1: select a suitable node from the left subtree of node 9 to replace node 9. It can be seen that node 8 meets the requirements;
Mode 2: select a suitable node from the right subtree of node 9 to replace node 9, and it can be seen that node 10 meets the requirements;

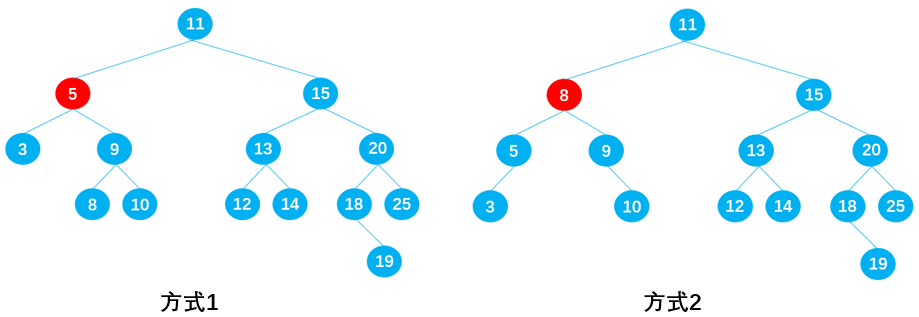
Delete node 7

There are also two ways to ensure that the original binary tree is still a binary search tree after node 7 is deleted:

Method 1: select a suitable node from the left subtree of node 7 to replace node 7. It can be seen that node 5 meets the requirements;
Mode 2: select a suitable node from the right subtree of node 7 to replace node 7, and it can be seen that node 8 meets the requirements;

Delete node 15

On the premise that the binary tree of the original tree is still a binary search tree after node 15 is deleted, there are also two ways:

Method 1: select a suitable node from the left subtree of node 15 to replace node 15. It can be seen that node 14 meets the requirements;
Method 2: select a suitable node from the right subtree of node 15 to replace node 15, and it can be seen that node 18 meets the requirements;

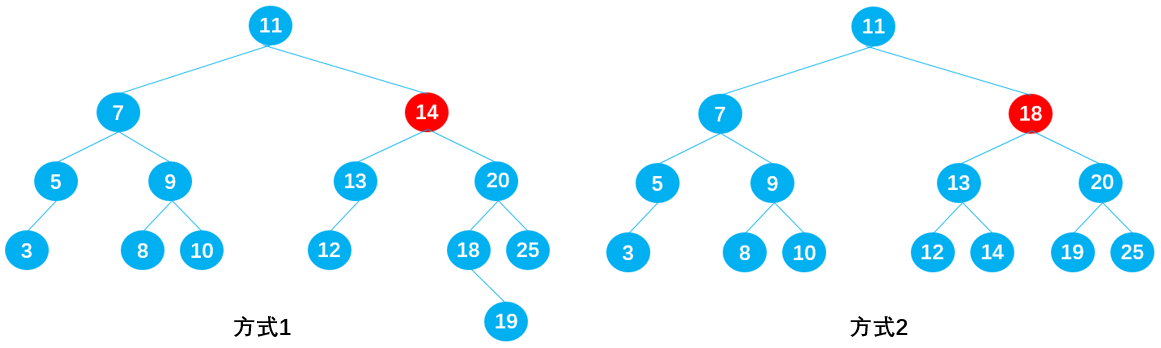
I believe you have found the law!

Rule summary: if the node to be deleted has two child nodes, or even child nodes, in this case, you need to find a suitable node from the child nodes below the node to be deleted to replace the current node.

If current is used to represent the node to be deleted, the appropriate node refers to:

The node in the left subtree of current that is a little smaller than current, that is, the maximum value in the left subtree of current;
The node slightly larger than current in the right subtree of current, that is, the minimum value in the right subtree of current;

Precursor & successor

In the binary search tree, these two special nodes have special names:

Nodes smaller than current are called precursors of current nodes. For example, node 5 in the following figure is the precursor of node 7;
A node a little larger than current is called the successor of current node. For example, node 8 in the following figure is the successor of node 7;

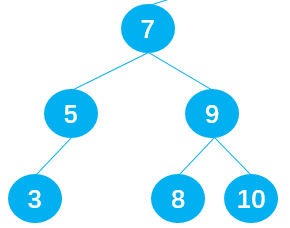
To find the successor of the node current that needs to be deleted, you need to find the minimum value in the right subtree of current, that is, traverse to the left in the right subtree of current;

When searching for precursors, you need to find the maximum value in the left subtree of current, that is, traverse the search to the right in the left subtree of current.

The following only discusses how to find the successor of current. The principle of finding the precursor is the same, which will not be discussed here for the time being.

Code implementation:

  // 3. A node with two child nodes is deleted
  } else {

    // 1. Find subsequent nodes
    let successor = this.getSuccessor(currentNode);

    // 2. Judge whether it is the root node
    if (currentNode === this.root) {
      this.root = successor;
    } else if (isLeftChild) {
      parentNode.left = successor;
    } else {
      parentNode.right = successor;
    }

    // 3. Change the subsequent left node to the deleted left node
    successor.left = currentNode.left;
  }
}

// Get subsequent nodes, that is, start from the right side of the node to be deleted to find the minimum value
getSuccessor(delNode) {

  // Define the variable and save the subsequent data to be found
  let successor = delNode;
  let current = delNode.right;
  let successorParent = delNode;

  // Loop through the right subtree node of current
  while (current !== null) {
    successorParent = successor;
    successor = current;
    current = current.left;
  }

  // Judge whether the found subsequent node is directly the right of the node to be deleted
  if (successor !== delNode.right) {
    successorParent.left = successor.right;
    successor.right = delNode.right;
  }
  return successor;
}

Complete implementation

// Delete node
remove(key) {

  let currentNode = this.root;
  let parentNode = null;
  let isLeftChild = true;

  // Cycle to find the node currentNode to be deleted, its parentNode and isLeftChild
  while (currentNode.key !== key) {

    parentNode = currentNode;

    // Less than, look left
    if (key < currentNode.key) {
      isLeftChild = true;
      currentNode = currentNode.left;

    } else {  // Otherwise, look to the right
      isLeftChild = false;
      currentNode = currentNode.right;
    }

    // If no equal nodes are found, false is returned
    if (currentNode === null) {
      return false;
    }

  }


  // 1. Leaf nodes are deleted
  if (currentNode.left === null && currentNode.right === null) {

    if (currentNode === this.root) {
      this.root = null;
    } else if (isLeftChild) {
      parentNode.left = null;
    } else {
      parentNode.right = null;
    }


    // 2. A node with only one child node is deleted
  } else if (currentNode.right === null) { // currentNode only has left node
    //--2.1. The currentNode only exists in the case of < left node >
    //----2.1.1. currentNode equals root
    //----2.1.2. parentNode.left equals currentNode
    //----2.1.3. parentNode.right equals currentNode

    if (currentNode === this.root) {
      this.root = currentNode.left;
    } else if (isLeftChild) {
      parentNode.left = currentNode.left;
    } else {
      parentNode.right = currentNode.left;
    }

  } else if (currentNode.left === null) { // currentNode has only the right node
    //--2.2. The currentNode only exists in the case of < right node >
    //----2.1.1 currentNode equals root
    //----2.1.1 parentNode.left equals currentNode
    //----2.1.1 parentNode.right equals currentNode

    if (currentNode === this.root) {
      this.root = currentNode.right;
    } else if (isLeftChild) {
      parentNode.left = currentNode.right;
    } else {
      parentNode.right = currentNode.right;
    }


    // 3. A node with two child nodes is deleted
  } else {

    // 1. Find subsequent nodes
    let successor = this.getSuccessor(currentNode);

    // 2. Judge whether it is the root node
    if (currentNode === this.root) {
      this.root = successor;
    } else if (isLeftChild) {
      parentNode.left = successor;
    } else {
      parentNode.right = successor;
    }

    // 3. Change the subsequent left node to the deleted left node
    successor.left = currentNode.left;
  }
}

// Get subsequent nodes, that is, start from the right side of the node to be deleted to find the minimum value
getSuccessor(delNode) {

  // Define the variable and save the subsequent data to be found
  let successor = delNode;
  let current = delNode.right;
  let successorParent = delNode;

  // Loop through the right subtree node of current
  while (current !== null) {
    successorParent = successor;
    successor = current;
    current = current.left;
  }

  // Judge whether the found subsequent node is directly the right of the node to be deleted
  if (successor !== delNode.right) {
    successorParent.left = successor.right;
    successor.right = delNode.right;
  }
  return successor;
}

Balanced tree

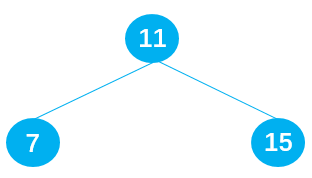
Defects of binary search tree: when the inserted data is orderly data, it will cause the depth of binary search tree to be too large. For example, the original binary search tree consists of 11 7 15, as shown in the following figure:

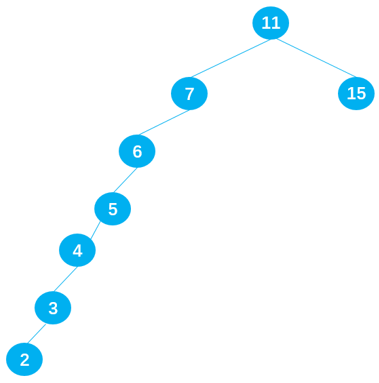
When inserting a set of ordered data: 6 5 4 3 2, it will become a search binary tree with too deep, which will seriously affect the performance of the binary search tree.

Nonequilibrium tree

For a better binary search tree, its data should be evenly distributed on the left and right.
However, after inserting continuous data, the data distribution in the binary search tree becomes uneven. We call this tree unbalanced tree.
For a balanced binary tree, the efficiency of operations such as insert / find is O(log n).
For an unbalanced binary tree, it is equivalent to writing a linked list, and the search efficiency becomes O(n).

Balance of trees

In order to operate a tree in a faster time O(log n), we need to ensure that the tree is always balanced:

At least most of them are balanced, and the time complexity is close to O(log n);
This requires that the number of descendant nodes on the left of each node in the tree should be equal to the number of descendant nodes on the right as much as possible;

Common balanced tree

AVL tree: it is the earliest kind of balance tree. It keeps the balance of the tree by storing an additional data in each node. Since AVL tree is a balanced tree, its time complexity is also O(log n). However, its overall efficiency is not as good as that of red black tree, and it is rarely used in development.
Red black tree: it also maintains the balance of the tree through some characteristics, and the time complexity is O(log n). When performing insert / delete operations, the performance is better than that of AVL tree, so the application of balance tree is basically red black tree.

stree

[external chain picture transferring... (img-O7Dut1dN-1638593676408)]

When inserting a set of ordered data: 6 5 4 3 2, it will become a search binary tree with too deep, which will seriously affect the performance of the binary search tree.

[external chain picture transferring... (img-jMHozPcV-1638593676408)]

Nonequilibrium tree

For a better binary search tree, its data should be evenly distributed on the left and right.
However, after inserting continuous data, the data distribution in the binary search tree becomes uneven. We call this tree unbalanced tree.
For a balanced binary tree, the efficiency of operations such as insert / find is O(log n).
For an unbalanced binary tree, it is equivalent to writing a linked list, and the search efficiency becomes O(n).

Balance of trees

In order to operate a tree in a faster time O(log n), we need to ensure that the tree is always balanced:

At least most of them are balanced, and the time complexity is close to O(log n);
This requires that the number of descendant nodes on the left of each node in the tree should be equal to the number of descendant nodes on the right as much as possible;

Common balanced tree

AVL tree: it is the earliest kind of balance tree. It keeps the balance of the tree by storing an additional data in each node. Since AVL tree is a balanced tree, its time complexity is also O(log n). However, its overall efficiency is not as good as that of red black tree, and it is rarely used in development.
Red black tree: it also maintains the balance of the tree through some characteristics, and the time complexity is O(log n). When performing insert / delete operations, the performance is better than that of AVL tree, so the application of balance tree is basically red black tree.

Posted by bam2550 on Sun, 05 Dec 2021 00:54:35 -0800

Programmer Group

13_JavaScript data structure and algorithm binary search tree

JavaScript data structure and algorithm (XIII) binary search tree

Binary search tree

Application example of binary search tree

Encapsulation of binary search tree

Common operations of binary search tree:

insert data

Traversal data

Preorder traversal

Medium order traversal

Postorder traversal

summary

Find data

Find maximum or minimum

Find a specific value

Delete data

The leaf node is deleted

A node with only one child node is deleted

A node with two child nodes is deleted

Precursor & successor

Complete implementation

Balanced tree

Hot Keywords