The main idea of the topic

The headquarters generals plan to deploy their artillery units on the NM grid map. An NM map is composed of N rows and M columns. Each grid of the map may be mountainous (represented by "H") or plain (represented by "P"), as shown below. At most one artillery unit can be deployed on each plain terrain (artillery units cannot be deployed on the mountain); the attack range of one artillery unit on the map is shown in the black area in the figure: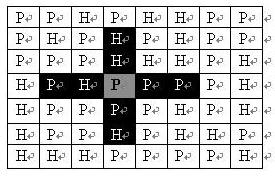

If an artillery unit is deployed on the plain marked by gray in the map, the black grid in the map indicates the area it can attack: two grids on the left and right along the horizontal direction, two grids on the top and two grids on the bottom along the vertical direction. No other white grid in the picture can attack. It can be seen from the picture that the artillery's attack range is not affected by the terrain.

Now, the generals plan how to deploy the Artillery Force. On the premise of preventing accidental injury (to ensure that no two artillery forces can attack each other, that is, no one artillery force is within the attack range of other Artillery Forces), how many artillery units of our army can be placed in the whole map area at most.

Input

The first line contains two positive integers separated by spaces, representing N and M respectively;
The next N lines contain consecutive M characters ('P 'or' H ') with no spaces in between. Represents the data for each row in the map in order. N <= 100；M <= 10.

Output

Only one line, containing an integer K, represents the maximum number of artillery units that can be placed.
Sample Input

5 4
PHPP
PPHH
PPPP
PHPP
PHHP

Sample Output

6

thinking

A sense of state compression surged to my heart after reading the question. Why? And m means that the number of rows is less than or equal to 10, and there are only two situations on each grid, i.e. put or not put
It's natural to think of DP
One more thing is important:
Only the plain can be used for artillery.
So we need to match the relationship between artillery firing and plain

Here is the DP thinking process:

• Definition.. We need to consider the definition. We can define dp[i][j][k] to represent the maximum number of schemes when the state of line I is j and the state of the previous line is K
• initialization.. Then we need to consider initialization, because the state must be pushed from the first two lines, so we need to deal with the number of schemes in the first two lines separately
• Transfer equation.. If you choose the largest one, you must compare it with your original self and the previous state + growth, and choose the larger one

First of all, we must have such a for loop

for (int i = 3; i < N; i++) {//Enumerate to line i
	//Condition of state transition
	for (int k = 0; k < cnt; k++) {//Enumerate all States on line i
		//Condition of state transition
		for (int m = 0; m < cnt; m++) {//Enumerate all States on line i-1
			//Condition of state transition
			for (int n = 0; n < cnt; n++) {//Enumerate all States on line i-2
				//Condition of state transition
				dp[i][k][m] = max(dp[i][k][m], dp[i - 1][m][n] + num[k]);
			}
		}
	}
}

The num[s]num[s]num[s] array is preprocessed by us. How many artillery (in fact, the number of binary bit 1) are arranged in the record state sss. Cnt cntcntcnt is the total number of all States, related to the value of MMM. It can be seen that there are state transition conditions that have not been handled. What state transition conditions do we have?

• The arranged artillery can't be on the hill - solution: when inputting, record each line of terrain in the array mmap. For example, if a line of terrain is "PHPP", then our mmap stores "0100". When we judge whether a state conflicts with the terrain, we just need to place the state and the terrain in the same place, for example, state 10111011 & 0100 = 0, which means that there is no place with hills Artillery!

	for (int i = 0; i < N; i++) {
		for (int j = 0; j < M; j++) {
			cin >> s;
			if (s == 'H') mmap[i] |= 1 << j;
		}
	}

• Then there is another problem, that is, the cannibalism of artillery. How to judge whether the range of artillery between two states does not overlap? For example, the first line is 1011, the second line is 0100 (assuming the terrain is qualified). Similarly, if it is 0, there is no position coverage. Therefore, the first line i-1 should judge whether it is hurt by the first line i-2 should judge whether it is hurt by the first two lines.

Then we complete the for loop

for (int i = 3; i < N; i++) {//Enumerate to line i
	for (int k = 0; k < cnt; k++) {//Enumerate all States on line i
		//The terrain conflict between states k and i
		if (S[k] & mmap[i]) continue;
		for (int m = 0; m < cnt; m++) {//Enumerate all States on line i-1
			//The terrain conflict between state m and i-1 or mutual damage with line i
			if ((S[m] & mmap[i - 1]) || (S[m] & S[k])) continue; 
			for (int n = 0; n < cnt; n++) {//Enumerate all States on line i-2
				//State n conflicts with the terrain of i-2 or injures each other with line i-1, or injures each other with line i
				if ((S[n] & mmap[i - 2]) || (S[n] & S[m]) || (S[n] & S[k]))  continue;
				dp[i][k][m] = max(dp[i][k][m], dp[i - 1][m][n] + num[k]);
			}
		}
	}
}

As you may have seen, we don't consider whether the rows hurt each other. Next, we will solve this problem. For the state array S, we preprocess all available states (conflicting states among rows) at the beginning of the program, and count their number cnt. In this way, we can not only avoid conflicts within a row, but also simplify them Number of states. count1 counts the number of binary number 1 of i

	S[0] = 0;
	for (int i = 1; i < (1 << M); i++) {
		if (i&(i << 1) || i & (i >> 1))continue;//Adjacent elements on the left and right
		if (i&(i << 2) || i & (i >> 2))continue;//Left 2 right 2 has adjacent elements
		S[cnt] = i;
		num[cnt++] = count1(i);
	}

It is worth noting that the main for loop starts from the third line, and the first and second lines should be handled separately

	for (int k = 0; k < cnt; k++) {
		if (S[k] & mmap[0])continue;//Terrain conflict
		dp[0][k][0] = num[k];
	}

	for (int k = 0; k < cnt; k++) {//first line
		if (S[k] & mmap[1]) continue;
		for (int m = 0; m < cnt; m++) {//Zero line
			if ((S[k] & mmap[0]) || (S[k] & S[m])) continue;
			dp[1][m][k] = max(dp[1][m][k], dp[0][k][0] + num[m]);
		}
	}

Finally, only the last row of dp array needs to be counted to find the largest element value.

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;

#define ll int
#define MAX	15

//cnt: total available states S: all available states
ll N, M, cnt = 1, S[1025];

//dp: movement group; num: number of artillery in each state; mmap: terrain corresponding to each line
ll dp[105][70][70], num[1025], mmap[105];

int count1(int k) {
	int ans = 0;
	while (k > 0) {
		ans++;
		k -= k & (-k);//K & (- K): the decimal number corresponding to the last bit 1 of K
	}
	return ans;
}

int main() {
	cin >> N >> M; char s;
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < M; j++) {
			cin >> s;
			if (s == 'H') mmap[i] |= 1 << j;
		}
	}

	S[0] = 0;
	for (int i = 1; i < (1 << M); i++) {
		if (i&(i << 1) || i & (i >> 1))continue;//Adjacent elements on the left and right
		if (i&(i << 2) || i & (i >> 2))continue;//Left 2 right 2 has adjacent elements
		S[cnt] = i;
		num[cnt++] = count1(i);
	}

	for (int k = 0; k < cnt; k++) {
		if (S[k] & mmap[0])continue;//Terrain conflict
		dp[0][k][0] = num[k];
	}

	for (int k = 0; k < cnt; k++) {//first line
		if (S[k] & mmap[1]) continue;
		for (int m = 0; m < cnt; m++) {//Zero line
			if ((S[m] & mmap[0]) || (S[k] & S[m])) continue;
			dp[1][k][m] = max(dp[1][k][m], dp[0][m][0] + num[k]);
		}
	}

	for (int i = 2; i < N; i++) {//Enumerate to line i
		for (int k = 0; k < cnt; k++) {//Enumerate all States on line i
			//The terrain conflict between states k and i
			if (S[k] & mmap[i]) continue;
			for (int m = 0; m < cnt; m++) {//Enumerate all States on line i-1
				//The terrain conflict between state m and i-1 or mutual damage with line i
				if ((S[m] & mmap[i - 1]) || (S[m] & S[k])) continue; 
				for (int n = 0; n < cnt; n++) {//Enumerate all States on line i-2
					//State n conflicts with the terrain of i-2 or injures each other with line i-1, or injures each other with line i
					if ((S[n] & mmap[i - 2]) || (S[n] & S[m]) || (S[n] & S[k]))  continue;
					dp[i][k][m] = max(dp[i][k][m], dp[i - 1][m][n] + num[k]);
				}
			}
		}
	}

	ll res = 0;
	for (ll i = 0; i < cnt; i++) {
		for (ll j = 0; j < cnt; j++) {
			res = max(res, dp[N - 1][i][j]);
		}
	}
	cout << res << endl;
}

Of course, the storage space can be further optimized. Why dp can be turned on 70 * 70 here is because we first need to filter the status and select the available CNTs, which will not exceed 70. Of course, you can use the rolling array group to further optimize the memory.